8 Vectorización de funciones
R trabaja de forma vectorizada, eso significa que la mayoría de procedimientos (o funciones) quedan vectorizadas por naturaleza y por esa razón podemos evaluar una función en un único valor o en un vector, y el resultado será el resultado esperado.
Sin embargo, en algunas situaciones la vectorización no está garantizada y por eso al evaluar nuestra función en un vector, el resultado no coincide con lo esperado. En el siguiente ejemplo vamos a ver un caso de una función NO vectorizada.
Ejemplo
Construya una función que reciba los coeficientes de una ecuación de segundo grado \(ax^2+bx+c=0\) y que entregue las dos raices.
Solución
Recordemos que la solución de una ecuación de segundo grado es:
\[ x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} \]
Vamos a crear la función solicitada así:
raices1 <- function(a, b, c) {
raiz1 <- (-b - sqrt(b^2-4*a*c)) / (2*a)
raiz2 <- (-b + sqrt(b^2-4*a*c)) / (2*a)
return(c(raiz1, raiz2))
}Ahora vamos a probar la función raices1 para tres casos pero lo vamos a realizar de forma individual. Los tres casos son:
- \(x^2+4x=0\).
- \(x^2+x+2=0\).
- \(x^2+2x-3=0\).
## [1] -4 0## [1] -2 -1## [1] -3 1Ahora vamos a probar nuestra función ingresando los tres valores de \(a\), \(b\) y \(c\) en forma de vectores así:
## [1] -4 -2 -3 0 -1 1Al ver la salida vemos que el resultado no es el esperado, si salen los números pero NO en el orden que esperamos, eso nos podría confundir a nosotros y a los nuevos usuarios de nuestra función raices1.
¿Qué debemos hacer para garantizar la vectorización?
8.1 Forma 1: asegurando la vectorización desde el origen
Lo primero es crear una función auxiliar que reciba un vector y no valores separados. Es decir, la función recibe los tres valores por medio del vector x y luego dentro de la función se crean los valores a, b y c necesarios. A continuación la función auxiliar.
raiz_aux <- function(x) {
a <- x[1]
b <- x[2]
c <- x[3]
raiz1 <- (-b - sqrt(b^2-4*a*c)) / (2*a)
raiz2 <- (-b + sqrt(b^2-4*a*c)) / (2*a)
return(c(raiz1, raiz2))
}La clave para crear la función vectorizada raices2 es que ella reciba los valores de los coefientes por separado, internamente se construya un matriz m con los valores individuales (o vectores) que ingrese al usuario, y a esa matriz m se le aplique por filas la función auxiliar raiz_aux para obtener las raices. Abajo el código para la nueva versión de la función pero vectorizada.
raices2 <- function(a, b, c) {
m <- cbind(a, b, c)
res <- apply(X=m, MARGIN=1, FUN=raiz_aux)
rownames(res) <- c("raiz 1", "raiz 2")
return(t(res))
}Esta nueva función funciona bien si el usuario ingresa los coeficientes de una sola ecuación \(ax^2+bx+c=0\) o si ingresa los coeficientes de varias ecuaciones. Hagamos pruebas para asegurarnos de la vectorización.
## raiz 1 raiz 2
## [1,] -4 0## raiz 1 raiz 2
## [1,] -2 -1## raiz 1 raiz 2
## [1,] -3 1## raiz 1 raiz 2
## [1,] -4 0
## [2,] -2 -1
## [3,] -3 18.2 Forma 2: usando Vectorize
Hay una función básica llamada Vectorize que nos ayuda a crear funciones vectorizadas. Vamos a aplicar la función Vectorize sobre la función original raices1 para vectorizarla, a continuación el código:
Vamos a probar esta tercera versión de la función.
## [,1] [,2] [,3]
## [1,] -4 -2 -3
## [2,] 0 -1 1De la salida anterior vemos que los resultados de las funciones vectorizadas raices2 y raices3 coinciden.
8.3 Comparando los tiempos de procesamiento
Vamos a comparar los tiempos de procesamiento para 50 pruebas usando la función microbenchmark. Abajo el código necesario para la comparación.
library(microbenchmark)
res <- microbenchmark(vect_origen = raices2(a=1, b=4, c=0),
vect_Vector = raices3(a=1, b=4, c=0),
times = 50L)
res## Unit: microseconds
## expr min lq mean median uq max neval
## vect_origen 136.300 146.302 162.1271 158.9010 169.101 245.201 50
## vect_Vector 133.101 143.501 155.6989 152.9015 163.600 295.202 50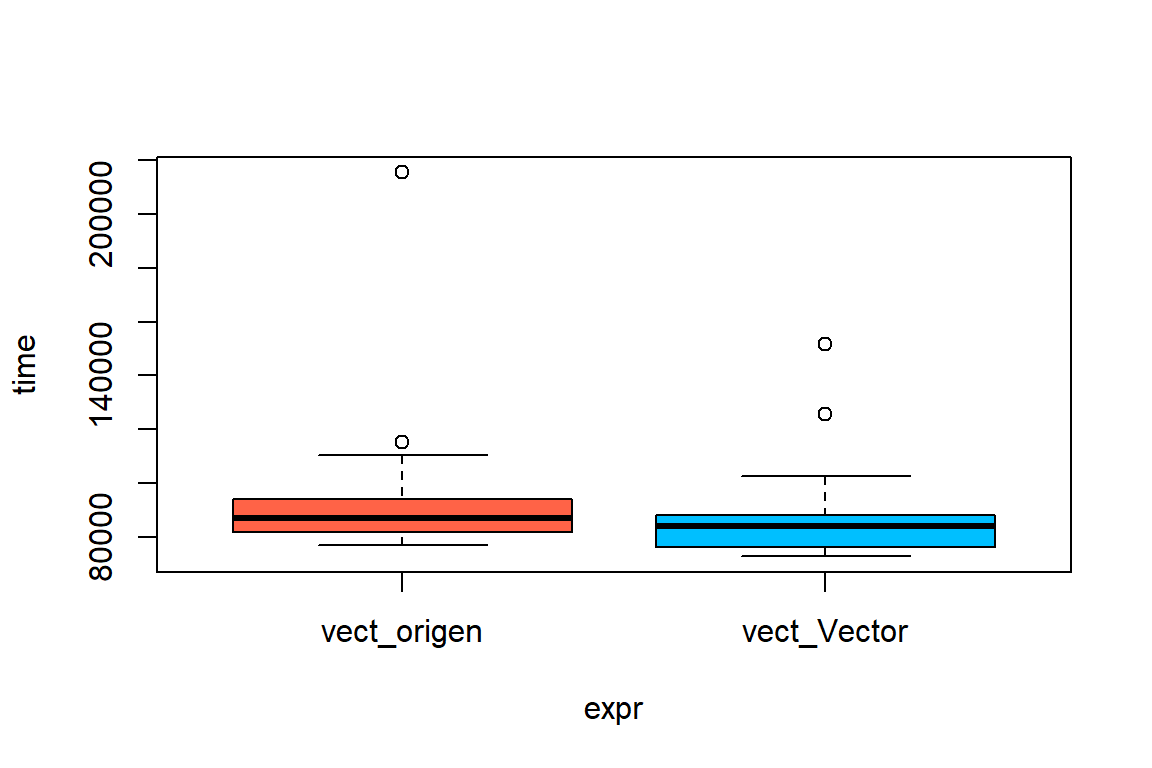
Los resultados anterior muestran que no hay mucha diferencia entre los tiempos de procesamiento de ambas funciones.
Vectorize para elegir la mejor opción.
8.4 Otros recursos para aprender sobre vectorización
- R inferno: https://www.burns-stat.com/pages/Tutor/R_inferno.pdf.
- R bloggers: https://www.r-bloggers.com/2019/04/vectorizing-functions-in-r-is-easy-2/
- Usando purrr: https://thatdatatho.com/vectorization-r-purrr/
- Otro recurso: https://cnuge.github.io/post/vectorize_r/
- Jim Hester: https://www.jimhester.com/post/2018-04-12-vectorize/