18 Distribuciones continuas

En este capítulo se mostrarán las funciones de R para distribuciones continuas.

18.1 Funciones disponibles para distribuciones continuas

Para cada distribución continua se tienen 4 funciones, a continuación el listado de las funciones y su utilidad.

dxxx(x, ...)  # Función de densidad de probabilidad, f(x)
pxxx(q, ...)  # Función de distribución acumulada hasta q, F(x)
qxxx(p, ...)  # Cuantil para el cual P(X <= q) = p
rxxx(n, ...)  # Generador de números aleatorios.

En el lugar de las letras xxx se de debe colocar el nombre de la distribución en R, a continuación el listado de nombres disponibles para las 11 distribuciones continuas básicas.

beta     # Beta
cauchy   # Cauchy
chisq    # Chi-cuadrada
exp      # Exponencial
f        # F
gamma    # Gama
lnorm    # log-normal
norm     # normal
t        # t-student
unif     # Uniforme
weibull  # Weibull

Combinando las funciones y los nombres se tiene un total de 44 funciones, por ejemplo, para obtener la función de densidad de probabilidad \(f(x)\) de una normal se usa la función dnorm( ) y para obtener la función acumulada \(F(x)\) de una Beta se usa la función pbeta( ).

18.2 Distribución beta

La distribución beta es muy útil para modelar fenómenos o variables que están en el intervalo \((0, 1)\). Algunas variables que se podrían modelar con la beta son: % de productos defectuosos, % de votantes por un candidato entre otros.

La función de densidad de la distribución beta es la siguiente

\[ f(x) = \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}x^{a-1}(1-x)^{b-1}, \]

donde \(0<x<1\), con parámetros que deben cumplir \(a>0\) y \(b>0\).

En la siguiente figura se muestran tres densidades de la beta para diferentes valores de los parámetros.

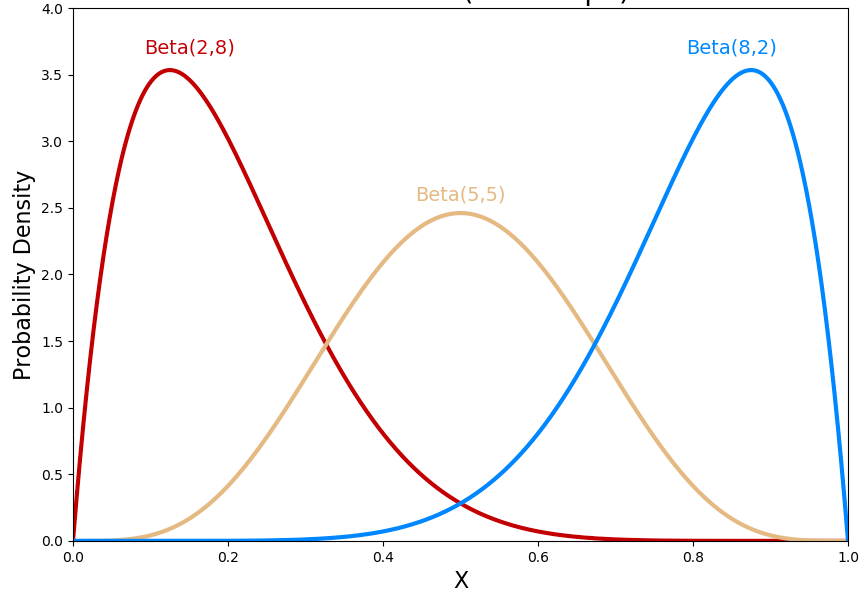
Figure 18.1: Ejemplo de tres densidades para la beta.

En R los parámetros \(a\) y \(b\) de la beta se escriben como shape1 y shape2 respectivamente.

Ejemplo beta

Considere que una variable aleatoria \(X\) se distribuye beta con parámetros \(a=2\) y \(b=5\).

1. Dibuje la densidad de la distribución.

La función dbeta sirve para obtener la altura de la curva de una distribución beta y combinándola con la función curve se puede dibujar la densidad solicitada. En la Figura 18.2 se presenta la densidad, observe que para la combinación de parámetros \(a=2\) y \(b=5\) la distribución es sesgada a la derecha.

curve(dbeta(x, shape1=2, shape2=5), lwd=3, las=1, ylab='Densidad')

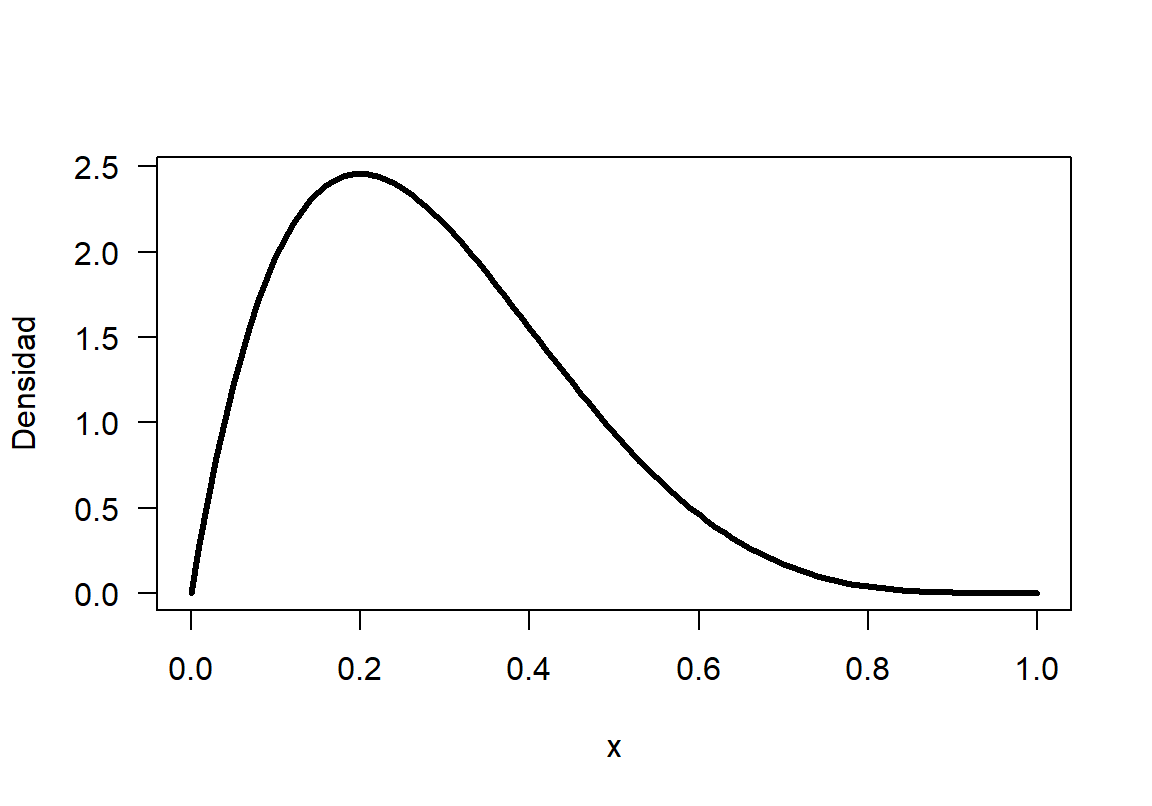
Figure 18.2: Función de densidad para una \(Beta(2, 5)\).

2. Calcular \(P(0.3 \leq X \leq 0.7)\).

Para obtener la probabilidad o área bajo la densidad se puede usar la función integrate, los límites de la integral se ingresan por medio de los parámetros lower y upper. Si la función a integrar tiene parámetros adicionales como en este caso, éstos parámetros se ingresan luego de los límites de la integral. A continuación el código necesario para obtener la probabiliad solicitada.

integrate(f=dbeta, lower=0.3, upper=0.7, shape1=2, shape2=5)

## 0.40924 with absolute error < 4.5e-15

Otra forma de obtener la probabilidad solicitada es restando de \(F(x_{max})\) la probabilidad \(F(x_{min})\). Las probabilidades acumuladas hasta un valor dado se obtienen con la función pbeta, a continuación el código necesario.

pbeta(q=0.7, shape1=2, shape2=5) - pbeta(q=0.3, shape1=2, shape2=5)

## [1] 0.40924

De ambas formas se obtiene que \(P(0.3 \leq X \leq 0.7)=0.4092\).

Recuerde que para distribuciones continuas

\[ P(a < X < b) = P(a \leq X < b) = P(a < X \leq b) = P(a \leq X \leq b)\]

18.3 Distribución exponencial

La distribución exponencial es muy útil para modelar fenómenos o variables que están en el intervalo \((0, \infty)\). Algunas variables que se podrían modelar con la exponencial son: duración de una batería, tiempo de sobrevivencia de un paciente luego de una cirugía, entre otros.

La función de densidad de la distribución exponecial es la siguiente

\[ f(x) = \lambda e^{-\lambda x}, \]

donde \(0<x<\infty\) con parámetro que deben cumplir \(\lambda>0\). El parámetro \(\lambda\) se le conoce como “rate”.

En la siguiente figura se muestran tres densidades de la exponecial para diferentes valores de los parámetros.

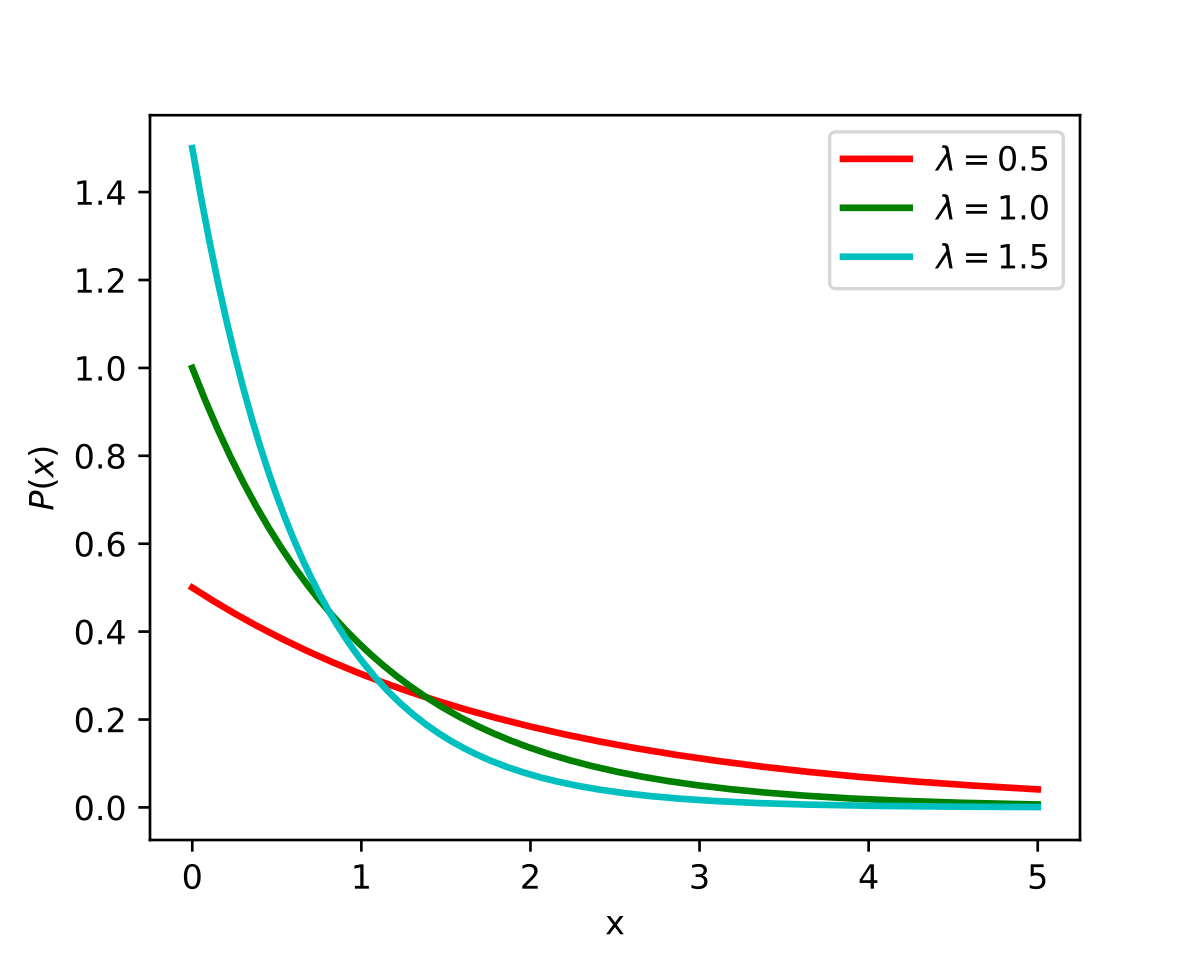
Figure 18.3: Ejemplo de tres densidades para la exponencial.

Ejemplo exponencial

Considere que una variable aleatoria \(X\) se distribuye exponencial con parámetro \(\lambda=2.5\).

1. Dibuje la densidad de la distribución.

La función dexp sirve para obtener la altura de la curva de una distribución exponencial y combinándola con la función curve se puede dibujar la densidad solicitada. En la Figura 18.4 se presenta la densidad.

curve(dexp(x, rate=2.5), lwd=3, las=1, ylab='Densidad', from=0, to=3)

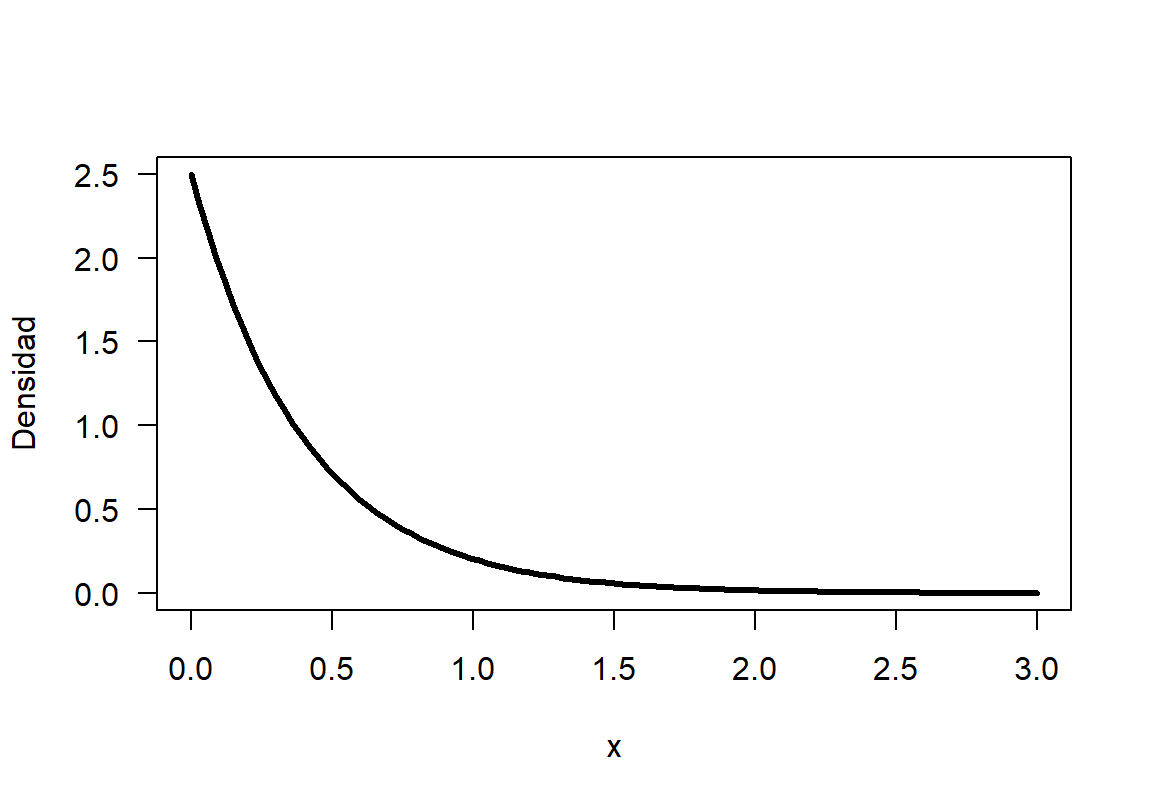
Figure 18.4: Función de densidad para una \(Exp(2.5)\).

2. Calcular \(P(0.5 \leq X \leq 1.5)\).

Para calcular la probabilidad podemos usar el siguiente código.

pexp(q=1.5, rate=2.5) - pexp(q=0.5, rate=2.5)

## [1] 0.2629871

Ejemplo normal estándar

Suponga que la variable aleatoria \(Z\) se distribuye normal estándar, es decir, \(Z \sim N(0, 1)\).

1. Calcular \(P(Z < 1.45)\).

Para calcular la probabilidad acumulada hasta un punto dado se usa la función pnorm y se evalúa en el cuantil indicado, a continuación el código usado.

pnorm(q=1.45)

## [1] 0.9264707

En la Figura 18.5 se muestra el área sombreada correspondiente a \(P(Z < 1.45)\).

2. Calcular \(P(Z > -0.37)\).

Para calcular la probabilidad solicitada se usa nuevamente la función pnorm evaluada en el cuantil dado. Como el evento de interés es \(Z > -0.37\), la probabilidad solicitada se obtiene como 1 - pnorm(q=-0.37), esto debido a que por defecto las probabilidades entregadas por la función pxxx son siempre a izquierda. A continuación el código usado.

1 - pnorm(q=-0.37)

## [1] 0.6443088

En la Figura 18.5 se muestra el área sombreada correspondiente a \(P(Z > -0.37)\).

Otra forma para obtener la probabilidad solicitada sin hacer la resta es usar el parámetro lower.tail para indicar que interesa la probabilidad a la derecha del cuantil dado, a continuación un código alternativo para obtener la misma probabilidad.

pnorm(q=-0.37, lower.tail=FALSE)

## [1] 0.6443088

3. Calcular \(P(-1.56 < Z < 2.58)\).

Para calcular la probabilidad solicitada se obtiene la probabilidad acumulada hasta 2.58 y de ella se resta lo acumulado hasta -1.56, a continuación el código usado.

pnorm(q=2.58) - pnorm(-1.56)

## [1] 0.93568

En la Figura 18.5 se muestra el área sombreada correspondiente a \(P(-1.56 < Z < 2.58)\).

4. Calcular el cuantil \(q\) para el cual se cumple que \(P(Z<q)=0.95\).

Para calcular el cuantil en el cual se cumple que \(P(Z<q)=0.95\) se usa la función qnorm, a continuación el código usado.

qnorm(p=0.95) 

## [1] 1.644854

En la Figura 18.5 se muestra el área sombreada correspondiente a \(P(Z<q)=0.95\).

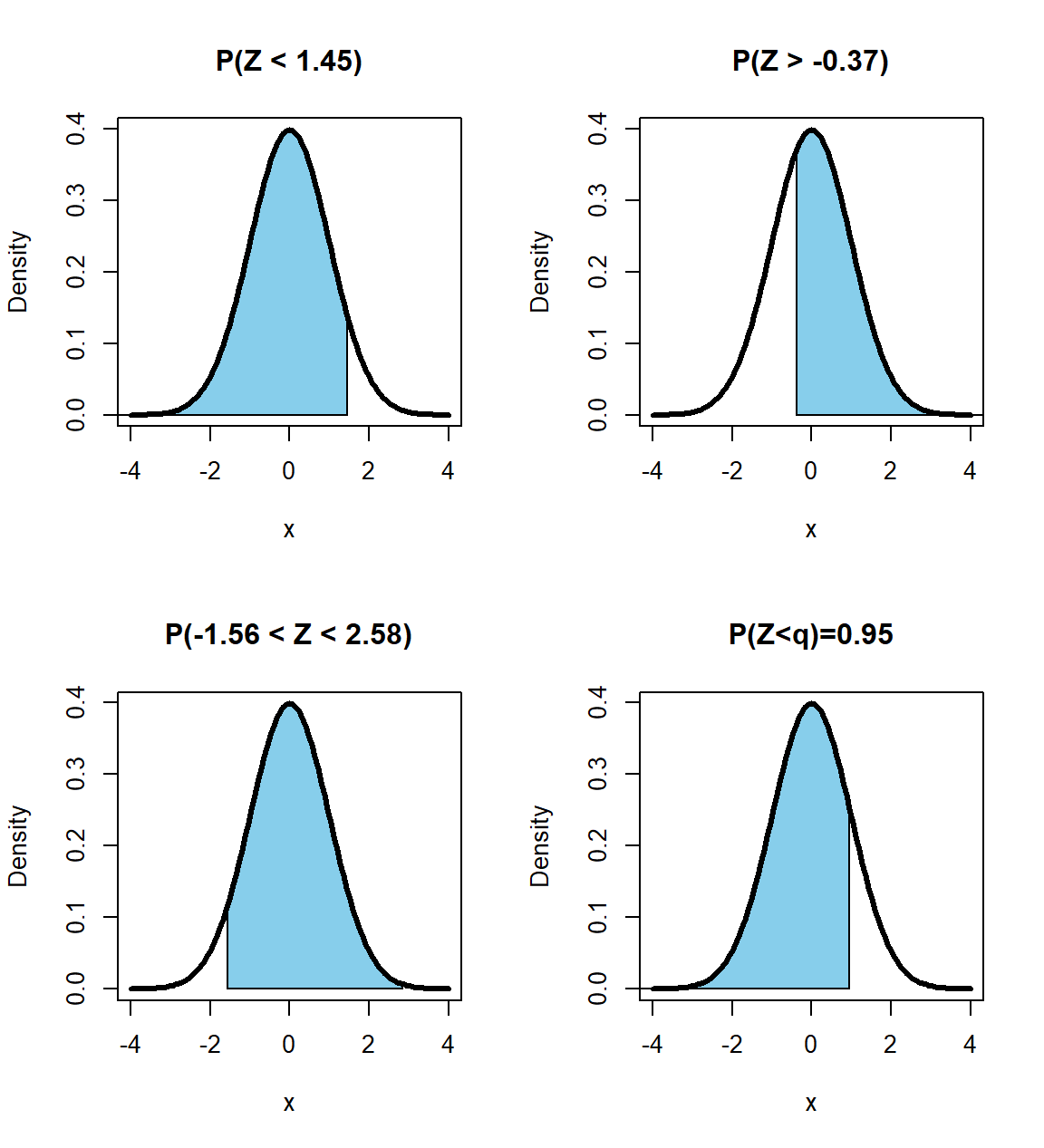
Figure 18.5: Área sombreada para los ejemplos.

El parámetro lower.tail es muy útil para indicar si estamos trabajando una cola a izquierda o una cola a derecha.

Ejemplo normal general

Considere un proceso de elaboración de tornillos en una empresa y suponga que el diámetro de los tornillos sigue una distribución normal con media de 10 \(mm\) y varianza de 4 \(mm^2\).

1. Un tornillo se considera que cumple las especificaciones si su diámetro está entre 9 y 11 mm. ¿Qué porcentaje de los tornillos cumplen las especificaciones?

Como se solicita probabilidad se debe usar pnorm indicando que la media es \(\mu=10\) y la desviación de la distribución es \(\sigma=2\). A continuación el código usado.

pnorm(q=11, mean=10, sd=2) - pnorm(q=9, mean=10, sd=2)

## [1] 0.3829249

2. Un tornillo con un diámetro mayor a 11 mm se puede reprocesar y recuperar. ¿Cuál es el porcentaje de reprocesos en la empresa?

Como se solicita una probabilidad a derecha se usa lower.tail=FALSE dentro de la función pnorm. A continuación el código usado.

pnorm(q=11, mean=10, sd=2, lower.tail=FALSE)

## [1] 0.3085375

3. El 5% de los tornillos más delgados no se pueden reprocesar y por lo tanto son desperdicio. ¿Qué diámetro debe tener un tornillo para ser clasificado como desperdicio?

Aquí interesa encontrar el cuantil tal que \(P(Diametro<q)=0.05\), por lo tanto se usa la función qnorm. A continuación el código usado.

qnorm(p=0.05, mean=10, sd=2)

## [1] 6.710293

4. El 10% de los tornillos más gruesos son considerados como sobredimensionados. ¿cuál es el diámetro mínimo de un tornillo para que sea considerado como sobredimensionado?

Aquí interesa encontrar el cuantil tal que \(P(Diametro>q)=0.10\), por lo tanto se usa la función qnorm pero incluyendo lower.tail=FALSE por ser una cola a derecha. A continuación el código usado.

qnorm(p=0.10, mean=10, sd=2, lower.tail=FALSE)

## [1] 12.5631

En la Figura 18.6 se muestran las áreas sombreadas para cada de las anteriores preguntas.

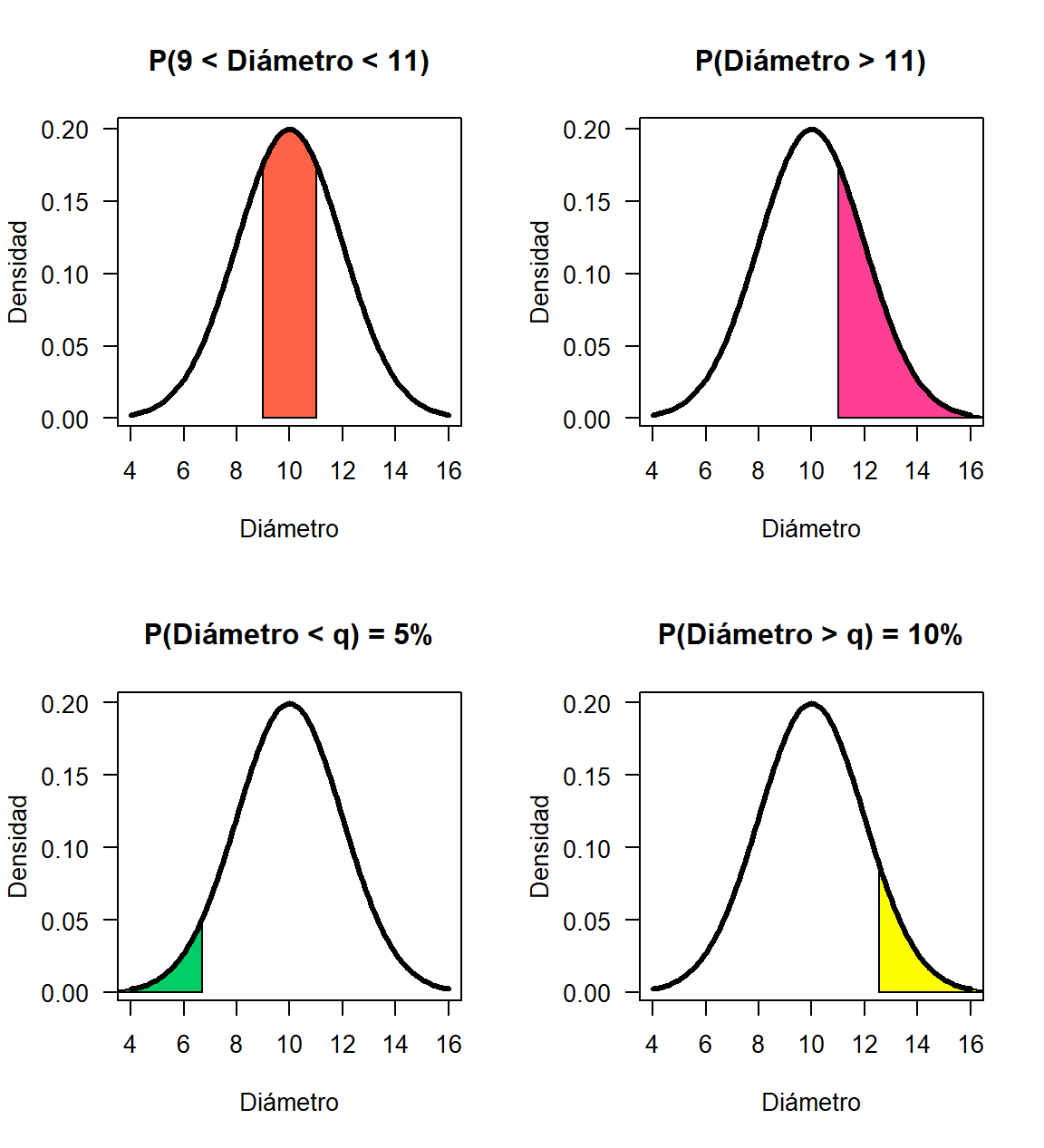
Figure 18.6: Área sombreada para el ejemplo de los tornillos.

18.4 Distribuciones continuas generales

En la práctica nos podemos encontramos con variables aleatorias continuas que no se ajustan a una de las distribuciones mostradas anteriormente, en esos casos, es posible manejar ese tipo de variables por medio de unas funciones básicas de R como se muestra en el siguiente ejemplo.

Ejemplo

En este ejemplo se retomará la base de datos crab sobre el cangrejo de herradura hembra presentado en el capítulo anterior. La base de datos crab contiene las siguientes variables: el color del caparazón, la condición de la espina, el peso en kilogramos, el ancho del caparazón en centímetros y el número de satélites o machos sobre el caparazón, la base de datos está disponible en el siguiente enlace.

1. Sea \(X\) la variable peso del cangrejo, dibuje la densidad para \(X\).

Para obtener la densidad muestral de un vector cuantitativo se usa la función density, y para dibujar la densidad se usa la función plot aplicada a un objeto obtenido con density, a continuación el código necesario para dibujar la densidad.

url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/crab'
crab <- read.table(file=url, header=T)

plot(density(crab$W), main='', lwd=5, las=1,
     xlab='Peso (Kg)', ylab='Densidad')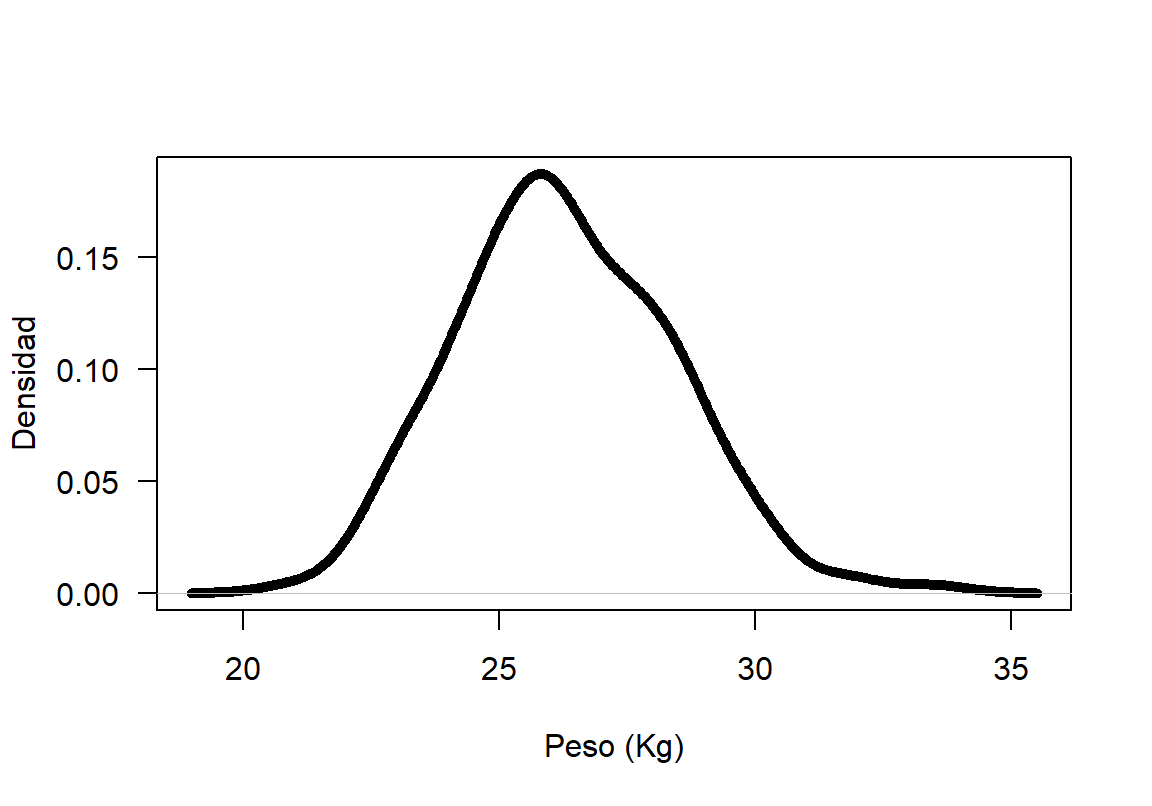

Figure 18.7: Función de densidad \(f(x)\) para el peso de los cangrejos.

En la Figura 18.7 se muestra la densidad para la variable peso de los cangrejos, esta densidad es bastante simétrica y el intervalo de mayor densidad está entre 22 y 30 kilogramos.

2. Dibujar \(F(x)\) para el peso del cangrejo.

Para dibujar la función \(F(x)\) se usa la función ecdf y se almacena el resultado en el objeto F, luego se dibuja la función deseada usando plot. A continuación el código utilizado. En la Figura 18.8 se presenta el dibujo para \(F(x)\).

F <- ecdf(crab$W)
plot(F, main='', xlab='Peso (Kg)', ylab='F(x)', cex=0.5, las=1)

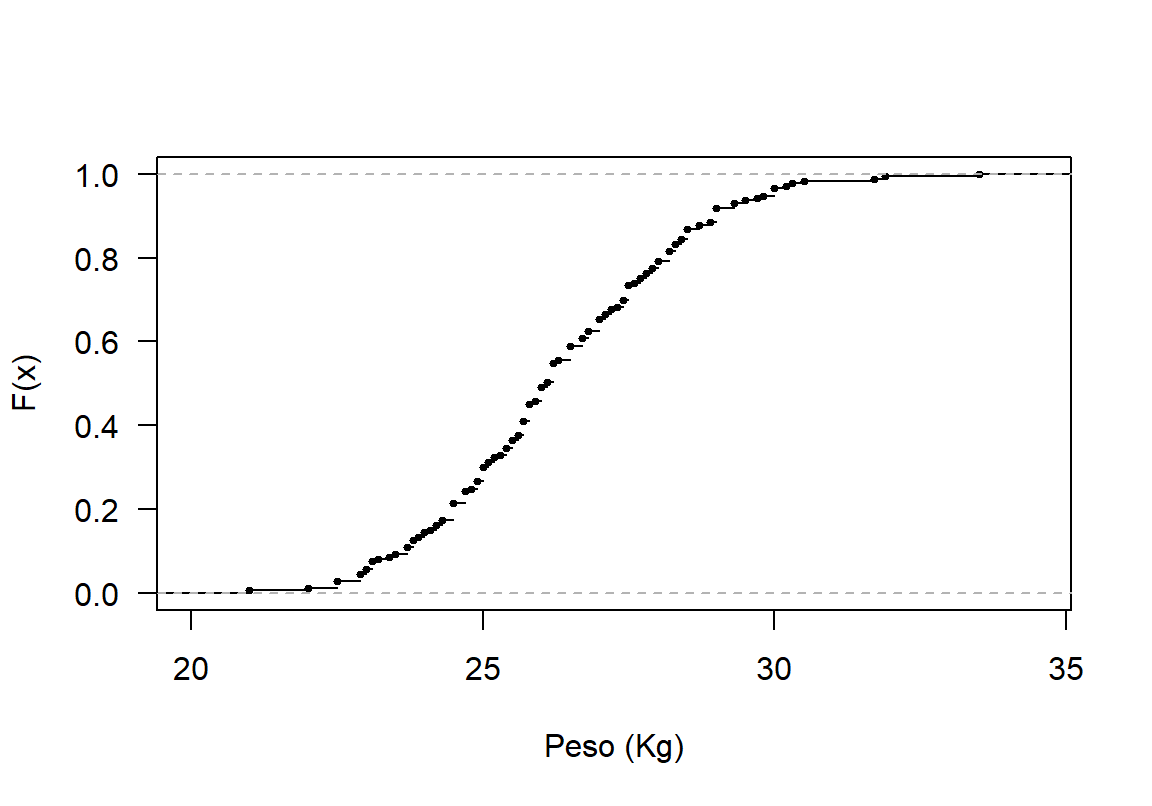
Figure 18.8: Función acumulada \(F(x)\) para el peso de los cangrejos.

3. Calcular la probabilidad de que un cangrejo hembra tenga un peso inferior o igual a 28 kilogramos.

Para obtener \(P(X \leq 28)\) se evalua en la función \(F(x)\) el cuantil 28 así.

F(28)

## [1] 0.7919075

Por lo tanto \(P(X \leq 28)=0.7919\).

4. Dibujar la función de densidad para el peso de los cangrejos hembra diferenciando por el color del caparazón.

Como son 4 los colores de los caparazones se deben construir 4 funciones de densidad. Usando la función split se puede partir el vector de peso de los cangrejos según su color. Luego se construyen las cuatro densidades usando la función density aplicada a cada uno de los pesos, a continuación el código.

pesos <- split(x=crab$W, f=crab$C)
f1 <- density(pesos[[1]])
f2 <- density(pesos[[2]])
f3 <- density(pesos[[3]])
f4 <- density(pesos[[4]])

Luego de tener las densidades muestrales se procede a dibujar la primera densidad con plot, luego se usa la funció lines para agregar a la densidad inicial las restantes densidades. En la Figura 18.9 se muestran las 4 densidades, una por cada color de caparazón.

plot(f1, main='', las=1, lwd=4,
     xlim=c(18, 34),
     xlab='Peso (Kg)', ylab='Densidad')
lines(f2, lwd=4, col='red')
lines(f3, lwd=4, col='blue')
lines(f4, lwd=4, col='orange')
legend('topright', lwd=4, bty='n',
       col=c('black', 'red', 'blue', 'orange'),
       legend=c('Color 1', 'Color 2', 'Color 3', 'Color 4'))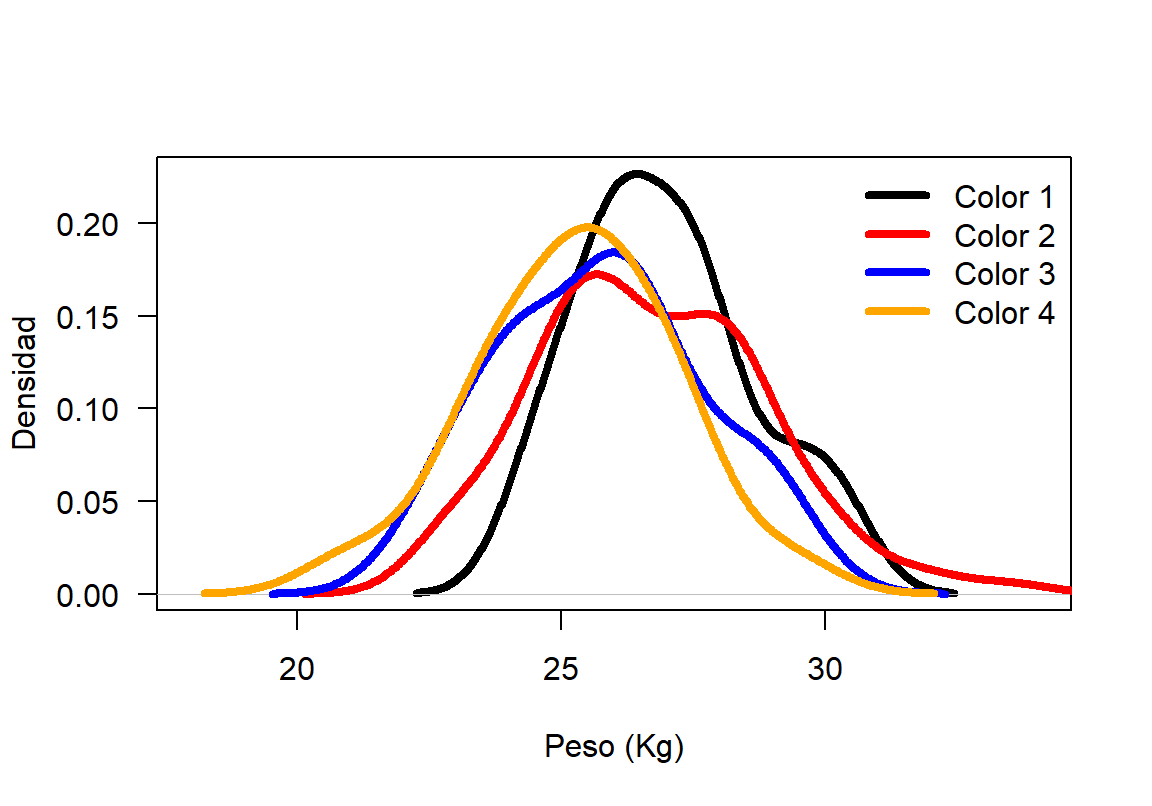

Figure 18.9: Función de densidad \(f(x)\) para el peso del cangrejo diferenciando por el color.

Otra forma para dibujar las densidades es usar el paquete ggplot2 (Wickham et al. 2024). En la Figura 18.10 se muestra el resultado obtenido de correr el siguiente código.

require(ggplot2)  # Recuerde que primero debe instalarlo

crab$Color <- as.factor(crab$C)  # Para convertir en factor

ggplot(crab, aes(x=W)) + 
  geom_density(aes(group=Color, fill=Color), alpha=0.3) +
  xlim(18, 34) + xlab("Peso (Kg)") + ylab("Densidad")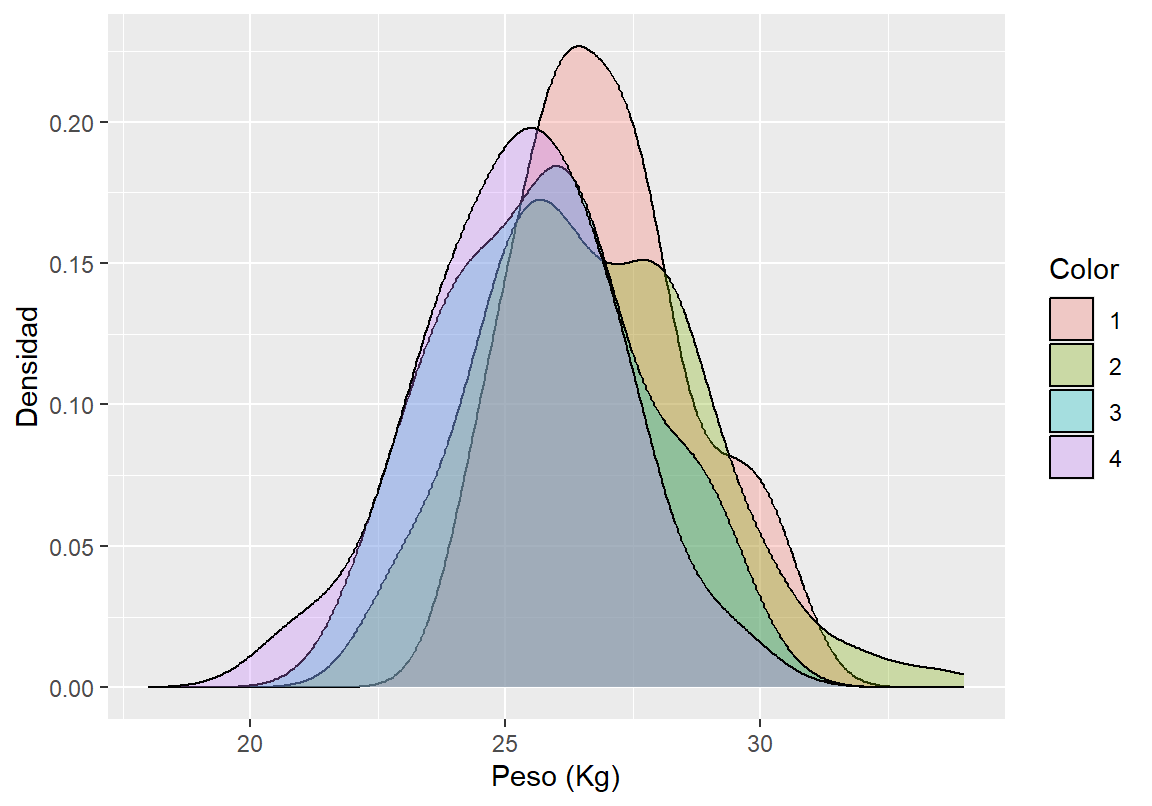

Figure 18.10: Función de densidad \(f(x)\) para el peso del cangrejo diferenciando por el color y usando ggplot2.

Para aprender más sobre el paquete ggplot2 se recomienda consultar este enlace.

References

Wickham, Hadley, Winston Chang, Lionel Henry, Thomas Lin Pedersen, Kohske Takahashi, Claus Wilke, Kara Woo, Hiroaki Yutani, Dewey Dunnington, and Teun van den Brand. 2024. Ggplot2: Create Elegant Data Visualisations Using the Grammar of Graphics. https://ggplot2.tidyverse.org.