12 Medidas de variabilidad

En este capítulo se mostrará cómo obtener las diferentes medidas de variabilidad con R.

Para ilustrar el uso de las funciones se utilizará la base de datos llamada aptos2015, esta base de datos cuenta con 11 variables registradas a apartamentos usados en la ciudad de Medellín. Las variables de la base de datos son:

  1. precio: precio de venta del apartamento (millones de pesos),
  2. mt2: área del apartamento (\(m^2\)),
  3. ubicacion: lugar de ubicación del aparamentos en la ciudad (cualitativa),
  4. estrato: nivel socioeconómico donde está el apartamento (2 a 6),
  5. alcobas: número de alcobas del apartamento,
  6. banos: número de baños del apartamento,
  7. balcon: si el apartamento tiene balcón (si o no),
  8. parqueadero: si el apartamento tiene parqueadero (si o no),
  9. administracion: valor mensual del servicio de administración (millones de pesos),
  10. avaluo: valor del apartamento en escrituras (millones de pesos),
  11. terminado: si el apartamento se encuentra terminado (si o no).

A continuación se presenta el código para definir la url donde están los datos, para cargar la base de datos en R y para mostrar por pantalla un encabezado (usando head) de la base de datos.

url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/aptos2015'
datos <- read.table(file=url, header=T)
head(datos)  # Para ver el encabezado de la base de datos
##   precio   mt2 ubicacion estrato alcobas banos balcon parqueadero
## 1     79 43.16     norte       3       3     1     si          si
## 2     93 56.92     norte       2       2     1     si          si
## 3    100 66.40     norte       3       2     2     no          no
## 4    123 61.85     norte       2       3     2     si          si
## 5    135 89.80     norte       4       3     2     si          no
## 6    140 71.00     norte       3       3     2     no          si
##   administracion   avaluo terminado
## 1          0.050 14.92300        no
## 2          0.069 27.00000        si
## 3          0.000 15.73843        no
## 4          0.130 27.00000        no
## 5          0.000 39.56700        si
## 6          0.120 31.14551        si

12.1 Rango

Para calcular el rango de una variable cuantitativa se usa la función range. Los argumentos básicos de la función range son dos y se muestran abajo.

range(x, na.rm = FALSE)

En el parámetro x se indica la variable de interés para la cual se quiere calcular el rango, el parámetro na.rm es un valor lógico que en caso de ser TRUE, significa que se deben remover las observaciones con NA, el valor por defecto para este parámetro es FALSE.

La función range entrega el valor mínimo y máximo de la variable que se ingresó, para obtener el valor de rango se debe restar del valor máximo el valor mínimo.

Ejemplo

Suponga que queremos obtener el rango para la variable precio de los apartamentos.

Solución

Para obtener el rango usamos el siguiente código.

range(datos$precio)
## [1]   25 1700

Otra forma de escribir el código anterior de forma secuencial es utilizando el operador pipe %>%. Este operador se puede leer como “entonces” y permite escribir código que cuenta una historia.

library(dplyr) # Para cargar el paquete dplyr
datos %>% select(precio) %>% range()
## [1]   25 1700
El código de arriba se puede leer así: Tome los datos, entonces seleccione el precio, entonces calcule el rango.

De la salida anterior podemos ver que los precios de los apartamentos van desde 25 hasta 1700 millones de pesos, es decir, el rango de la variable precio es sería igual 1700-25=1675 millones de pesos.

Ejemplo

Suponga que queremos obtener nuevamente el rango para la variable precio de los apartamentos pero diferenciando por el estrato.

Solución

Para calcular el rango (max-min) para el precio pero diferenciando por el estrato podemos usar el siguiente código.

datos %>% 
  group_by(estrato) %>% 
  summarise(el_rango=max(precio)-min(precio))
## # A tibble: 5 × 2
##   estrato el_rango
##     <int>    <dbl>
## 1       2      103
## 2       3      225
## 3       4      610
## 4       5     1325
## 5       6     1560
El código anterior se puede leer así: Tome los datos, entonces agrúpelos por estrato, entonces haga un resumen llamado el_rango que se obtiene como el resultado de restar el mínimo de precio al máximo de precio.

De los resultados podemos ver claramente que a medida que aumenta de estrato el rango del precio de los apartamentos aumenta. Apartamentos de estrato bajo tienden a tener precios similares mientras que los precios de venta para apartamentos de estratos altos tienden a ser muy diferentes entre si.

12.2 Varianza

La varianza es otra medida de qué tanto se alejan las observaciones \(x_i\) en relación al promedio y se mide en unidades cuadradas. Existen dos formas de calcular la varianza dependiendo de si estamos trabajando con una muestra o con la población.

La varianza muestral (\(S^2\)) se define así:

\[ S^2=\frac{\sum_{i=1}^{i=n}(x_i-\bar{x})^2}{n-1}, \]

donde \(\bar{x}\) representa el promedio muestral.

La varianza poblacional (\(\sigma^2\)) se define así:

\[ \sigma^2=\frac{\sum_{i=1}^{i=n}(x_i-\mu)^2}{n}, \]

donde \(\mu\) representa el promedio poblacional.

Para calcular la varianza muestral de una variable cuantitativa se usa la función var. Los argumentos básicos de la función var son dos y se muestran abajo.

var(x, na.rm = FALSE)

En el parámetro x se indica la variable de interés para la cual se quiere calcular la varianza muestral, el parámetro na.rm es un valor lógico que en caso de ser TRUE, significa que se deben remover las observaciones con NA, el valor por defecto para este parámetro es FALSE.

Ejemplo

Suponga que queremos determinar cuál ubicación en la ciudad presenta mayor varianza en los precios de los apartamentos y cuántos apartamentos hay en cada ubicación.

Solución

Como nos interesa calcular la varianza y hacer un conteo por cada ubicación, vamos a agrupar los datos por ubicación. Para realizar lo solicitado podemos utilizar el siguiente código.

datos %>% 
  group_by(ubicacion) %>% 
  summarize(n=n(),
            varianza=var(precio))
## # A tibble: 7 × 3
##   ubicacion          n varianza
##   <chr>          <int>    <dbl>
## 1 aburra sur       169    4169.
## 2 belen guayabal    67    2528.
## 3 centro            38    2588.
## 4 laureles          73   25351.
## 5 norte             10    1009.
## 6 occidente         69    3596.
## 7 poblado          268   84497.

De los resultados anteriores se nota que los apartamentos ubicados en el Poblado tienen la mayor variabilidad en el precio, este resultado se confirma al dibujar un boxplot para la variable precio dada la ubicación, en la Figura 12.1 se muestra el boxplot y se ve claramente la dispersión de los precios en el Poblado. El código usado para generar la Figura 12.1 se presenta a continuación.

with(datos, boxplot(precio ~ ubicacion, ylab='Precio (millones)'))
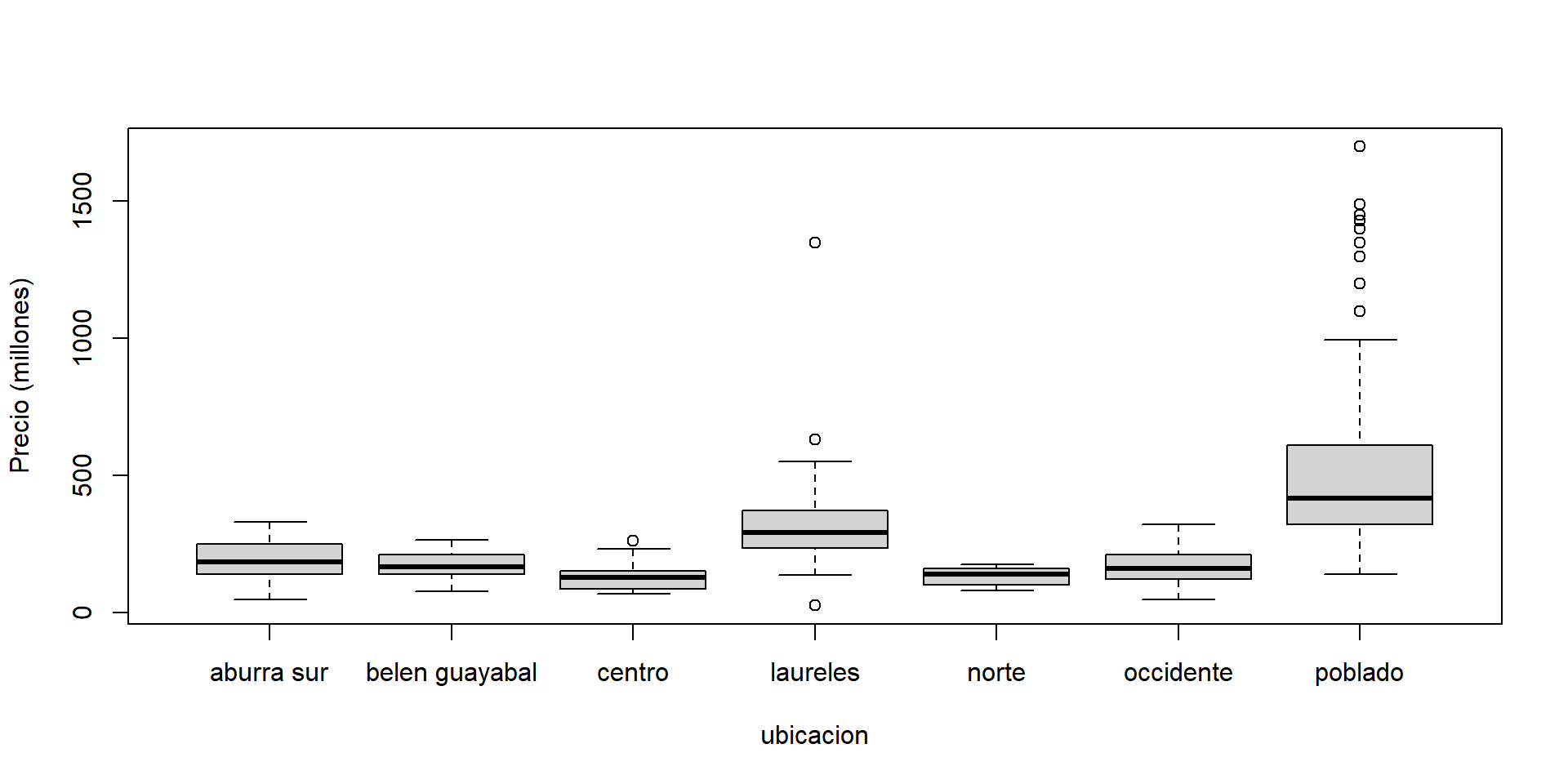
Boxplot para el precio de los apartamentos dada la ubicación.

Figure 12.1: Boxplot para el precio de los apartamentos dada la ubicación.

Ejemplo

¿Puedo aplicar la función var y la función sd a marcos de datos?

Solución

La respuesta es NO. La función sd se aplica sólo a vectores mientras que la función var de puede aplicar tanto a vectores como a marcos de datos. Al ser aplicada a marcos de datos numéricos se obtiene una matriz en que la diagonal representa las varianzas de las de cada una de las variables mientras que arriba y abajo de la diagonal se encuentran las covarianzas entre pares de variables.

Por ejemplo, si aplicamos la función var al marco de datos sólo con las variables precio, área y avaluo se obtiene una matriz de dimensión \(3 \times 3\), a continuación el código usado.

datos %>% 
  select(precio, mt2, avaluo) %>% 
  var()
##          precio       mt2    avaluo
## precio 61313.15 15874.107 33055.606
## mt2    15874.11  5579.417  9508.188
## avaluo 33055.61  9508.188 28588.853

De la salida anterior se observa que el resultado es una matriz de varianzas y covarianzas de dimensión \(3 \times 3\).

12.3 Desviación estándar

La desviación estándar es una medida de qué tanto se alejan las observaciones \(x_i\) en relación al promedio y se mide en las mismas unidades de la variable de interés. Existen dos formas de calcular la desviación estándar dependiendo de si estamos trabajando con una muestra o con la población.

La desviación estándar muestral (\(S\)) para \(n\) observaciones se define así:

\[ S=\sqrt{\frac{\sum_{i=1}^{i=n}(x_i-\bar{x})^2}{n-1}}, \] donde \(\bar{x}\) representa el promedio muestral.

La desviación estándar poblacional (\(\sigma\)) para \(n\) observaciones se define así:

\[ \sigma=\sqrt{\frac{\sum_{i=1}^{i=n}(x_i-\mu)^2}{n}}, \] donde \(\mu\) representa el promedio de la población.

Para calcular en R la desviación muestral (\(S\)) de una variable cuantitativa se usa la función sd, los argumentos básicos de la función sd son dos y se muestran a continuación.

sd(x, na.rm = FALSE)

En el parámetro x se indica la variable de interés para la cual se quiere calcular la desviación estándar muestral, el parámetro na.rm es un valor lógico que en caso de ser TRUE, significa que se deben remover las observaciones con NA, el valor por defecto para este parámetro es FALSE.

Ejemplo

Calcular la desviación estándar muestral (\(S\)) para la variable precio de los apartamentos.

Solución

Para obtener la desviación estándar muestral (\(S\)) solicitada usamos el siguiente código:

sd(x=datos$precio)
## [1] 247.6149

Ejemplo

Calcular la desviación estándar poblacional (\(\sigma\)) para el siguiente conjunto de 5 observaciones: 12, 25, 32, 15, 26.

Solución

Recordemos que las expresiones matemáticas para obtener \(S\) y \(\sigma\) son muy similares, la diferencia está en el denominador, para \(S\) el denominador es \(n-1\) mientras que para \(\sigma\) es \(n\). Teniendo esto en cuenta podemos construir nuestra propia función llamada Sigma que calcule la desviación poblacional. A continuación el código para crear nuestra propia función.

Sigma <- function(x) {
  n <- length(x)
  desvi <- sqrt(sum((x-mean(x))^2) / n)
  return(desvi)
}

Ahora para obtener la desviación estándar poblacional de los datos usamos el siguiente código.

y <- c(12, 25, 32, 15, 26)
Sigma(y)
## [1] 7.402702

12.4 Coeficiente de variación (\(CV\))

El coeficiente de variación se define como \(CV=s/\bar{x}\) y es muy sencillo de obtenerlo, la función coef_var mostrada abajo permite calcularlo.

coef_var <- function(x, na.rm = FALSE) {
  sd(x, na.rm=na.rm) / mean(x, na.rm=na.rm)
}

Ejemplo

Calcular el \(CV\) para el vector w definido a continuación.

w <- c(5, -3, NA, 8, 8, 7)

Solución

Vemos que el vector w tiene 6 observaciones y la tercera de ellas es un NA. Lo correcto aquí es usar la función coef_var definida antes pero indicándole que remueva los valores faltantes, para eso se usa el siguiente código.

coef_var(x=w, na.rm=T)
## [1] 0.9273618