16 Variables aleatorias
En este capítulo se mostrará como usar R para representar gráficamente variables aleatorias, calcular el valor esperado y obtener la varianza.
16.1 Variable aleatoria discreta
Una variable aleatoria discreta \(X\) definida en el espacio muestral \(S\) puede tomar valores en un conjunto finito o en un conjunto infinito pero contable. A continuación se presentan dos ejemplos.
- Si se lanzan tres monedas y se define \(Z\) como el número de caras menos el número de sellos, \(Z\) puede tomar valores de -3, -1, 1 y 3.
- Si lanza un balón de baloncesto a un aro y se define \(W\) como el número de lanzamientos fallidos antes de encestar la primera vez, \(W\) puede tomar valores de 0, 1, 2, 3, ….
Figure 16.1: Ejemplo de variables aleatorias discretas.
Sea \(X\) una variable aletoria discreta que toma valores en el conjunto \(D\) y con función de masa de probabilidad \(f(x)\). El valor esperado \(X\) se define como
\[ E(X) = \mu = \sum_{i \in D} x_i \, f(x_i) \] La varianza de la variable aleatoria \(X\) se define como
\[ Var(X) = \sigma^2 = \sum_{i \in D} (x_i-\mu)^2 \, f(x_i) \]
Ejemplo
Suponga que \(f(x)\) representa la función de masa de probabilidad dada por
\[ f(x) = \frac{2x+1}{25}, \quad x=0, 1, 2, 3, 4 \]
- Dibujar \(f(x)\).
- Dibujar \(F(x)\).
- Calcular \(E(X)\).
- Calcular \(Var(X)\).
- Calcular \(E(h(x))\) con \(h(x)=3x^2+x\).
Solución
Lo primero que debemos hacer es construir la función \(f(x)\).
Ahora vamos a verificar que es una función de masa de probabilidad, es decir, que los valores de \(f(x)>0\) y que la suma de las probabilidades es 1.
x_vals <- c(0, 1, 2, 3, 4) # Vector con los valores de X
probs <- f(x_vals) # Vector con P(X=x)=f(x)
cbind(x_vals, probs) # Tabla de X y P(X=x)## x_vals probs
## [1,] 0 0.04
## [2,] 1 0.12
## [3,] 2 0.20
## [4,] 3 0.28
## [5,] 4 0.36## [1] 1De la tabla anterior vemos que \(f(x) > 0\) y de la suma observamos que las probabilidades suman 1.
Vamos a dibujar la función de masa \(f(x)\) así:
plot(x=x_vals, y=probs, type="h",
lwd=3, col="blue", las=1,
xlab="X", ylab="f(X=x)")
grid() # Para incluir una rejilla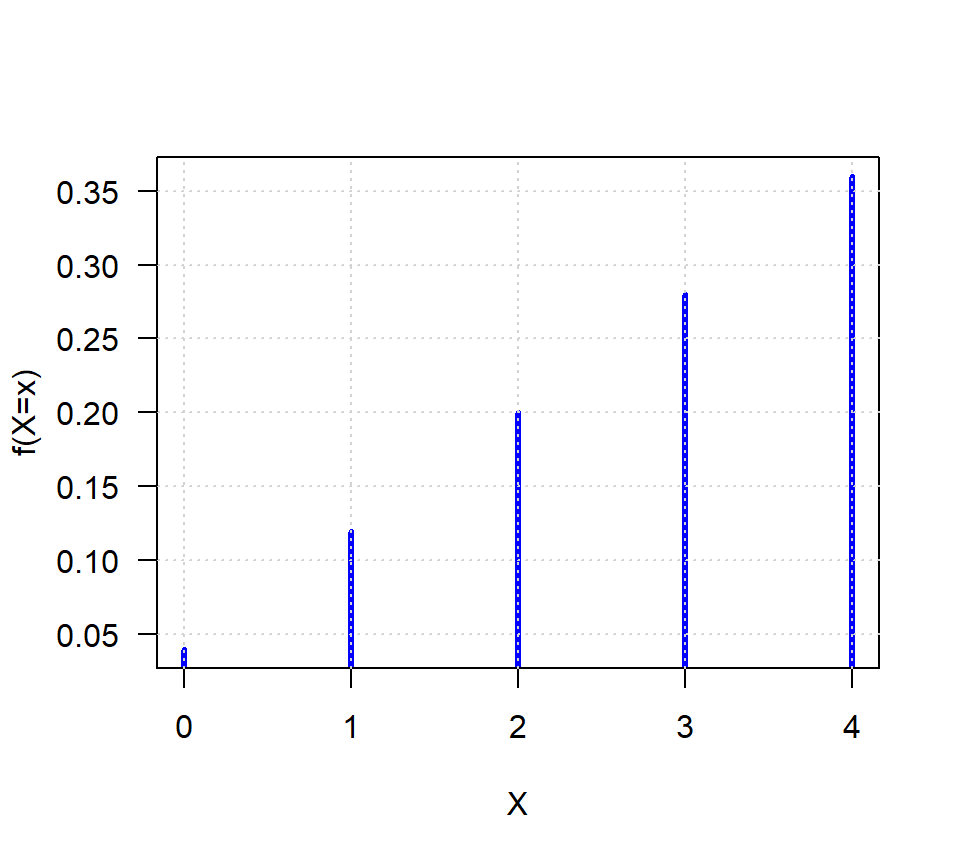
Figure 16.2: Función f(x) para el ejemplo.
Vamos a dibujar la función de masa \(F(x)\). Lo primero que se debe hacer es calcular las probabilidades acumuladas hasta cada valor que pueda tomar \(X\), para esto usamos la función cumsum aplicada al vector probs.
## [1] 0.04 0.16 0.36 0.64 1.00Ahora si podemos dibujar \(F(x)\) con la ayuda de la función stepfun.
# Para crear un objeto con la informacion para dibujar F(x)
F <- stepfun(x=x_vals, y=c(0, probs_acumul), right=TRUE)
# Para dibujar la funcion F(x)
plot(F, verticals=FALSE,
lwd=3, col="blue", las=1,
xlab="X", ylab="F(X=x)", main="")
grid() # Para incluir una rejilla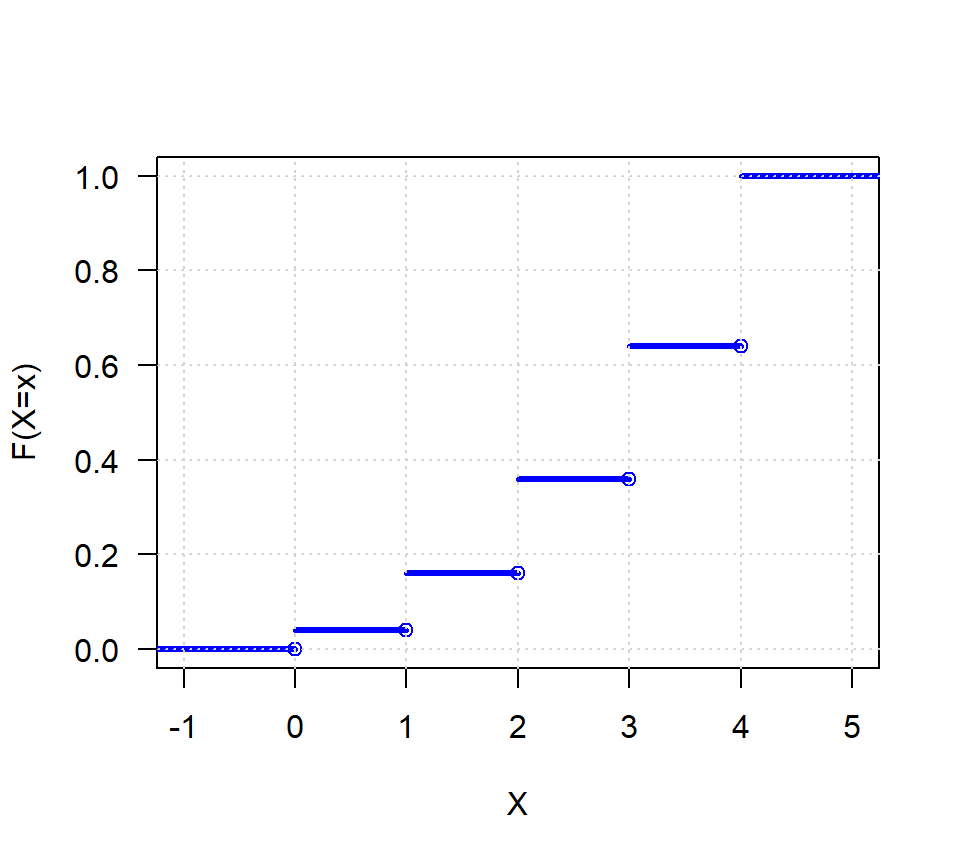
Figure 16.3: Función F(x) para el ejemplo.
Para calcular \(E(X)\) podemos usar el siguiente código.
## [1] 2.8Para calcular \(Var(X)\) podemos usar el siguiente código.
## [1] 1.36Para calcular \(E(h(x))\) con \(h(x)=3x^2+x\) podemos usar el siguiente código.
## [1] 30.416.2 App shiny pmf
En el enlace que se muestra abajo hay una aplicación llamada pmf que recibe una función de masa de probabilidad \(f(x)\) y ella entrega el dibujo de \(f(x)\), el dibujo de \(F(x)\), el \(E(X)\) y la \(Var(X)\).
16.3 Variable aleatoria continua
Una variable aleatoria continua \(X\) definida en el espacio muestral \(S\) se considera continua si ella puede tomar valores en los números reales \(\Re\). A continuación se presentan dos ejemplos.
- Se observa un vehículo en movimiento y se define \(Z\) como la velocidad al pasar por un punto.
- Se observa un grupo de personas corriendo una maratón y se define \(W\) como el tiempo necesario para hacer el recorrido.

Figure 16.4: Ejemplo de variables aleatorias continuas.
Sea \(X\) una variable aletoria continua que toma valores en el conjunto \(D\) y con función de masa de densidad \(f(x)\). El valor esperado \(X\) se define como
\[ E(X) = \mu = \int_{x \in D} x_i \, f(x_i) \] La varianza de la variable aleatoria \(X\) se define como
\[ Var(X) = \sigma^2 = \int_{x \in D} (x_i-\mu)^2 \, f(x_i) \]
Ejemplo
Suponga que \(f(x)\) representa la función de masa de densidad dada por
\[ f(x) = 20 e^{-20(x-12.5)}, \quad x>12.5 \]
- Dibujar \(f(x)\).
- Dibujar \(F(x)\).
- Calcular \(E(X)\).
- Calcular \(Var(X)\).
- Calcular \(E(h(x))\) con \(h(x)=3x^2+x\).
Solución
Lo primero que debemos hacer es construir la función \(f(x)\).
Ahora vamos a verificar que es una función de densidad de probabilidad, es decir, que el área bajo la curva es 1.
## 1 with absolute error < 1e-08Vamos a dibujar la función de densidad \(f(x)\) así:
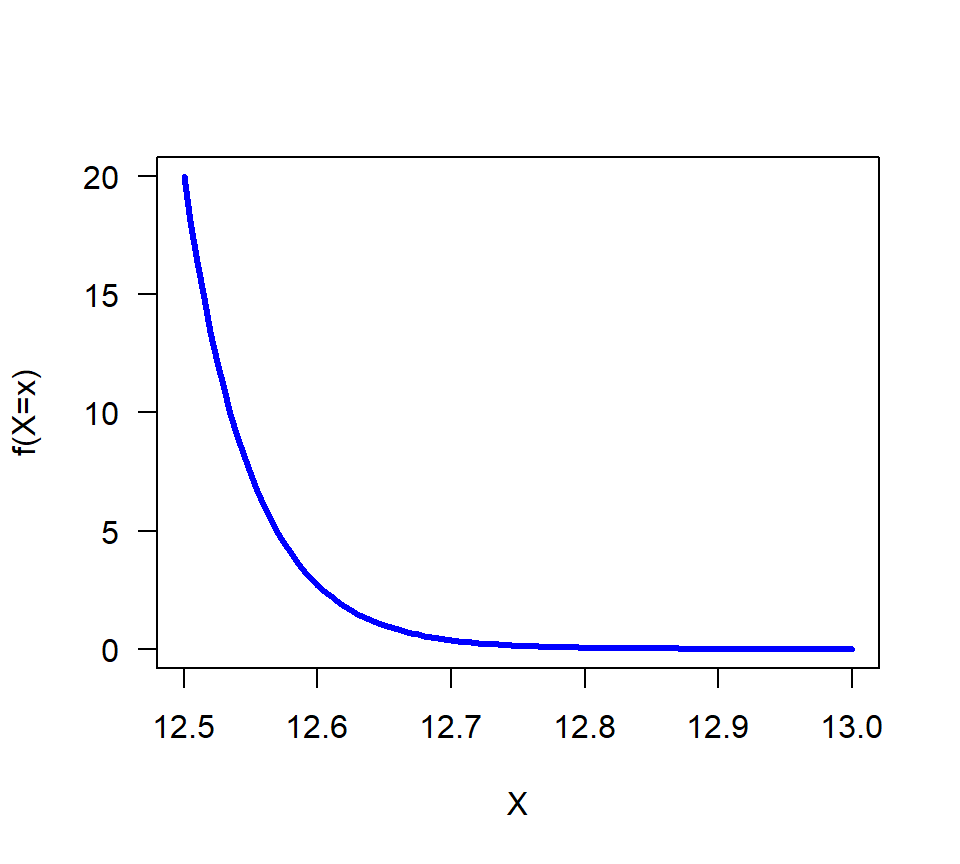
Figure 16.5: Función f(x) para el ejemplo 2.
La función \(F(x)\) la podemos obtener integrando la función \(f(x)\) de forma computacional así:
F <- function(x, a) integrate(f=f, lower=a, upper=x)$value
F <- Vectorize(F) # Para vectorizar la función y que pueda usar vectoresVamos a dibujar la función \(F(x)\) así:
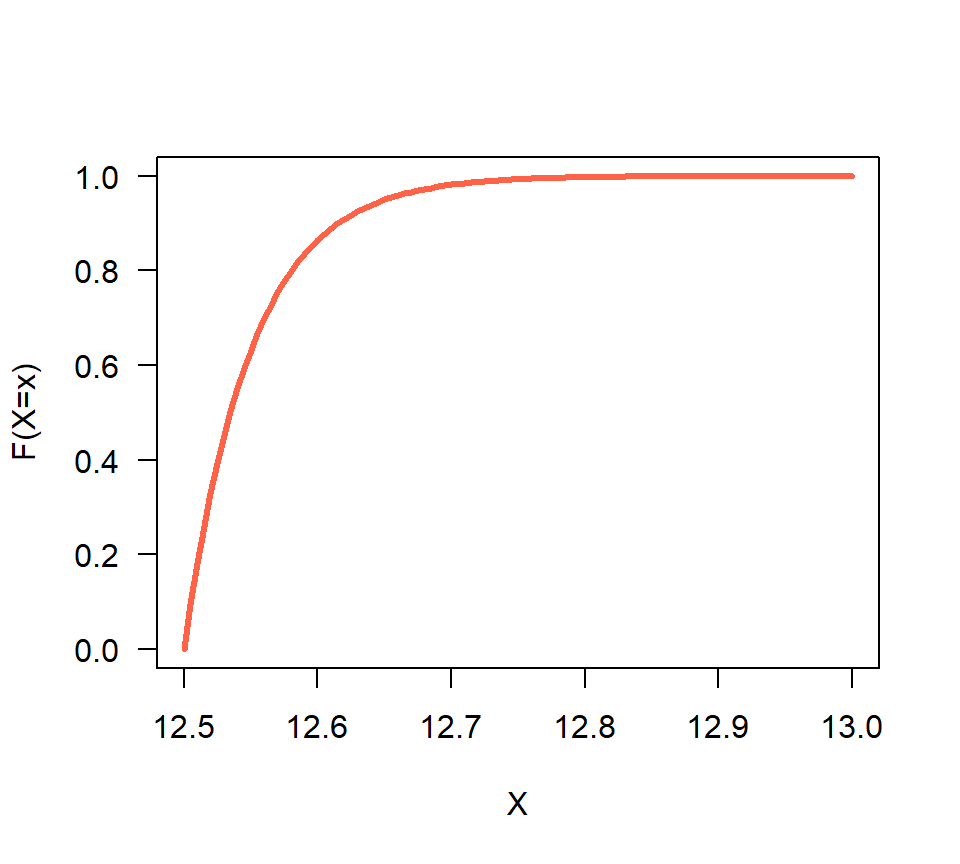
Figure 16.6: Función F(x) para el ejemplo 2.
Para obtener \(E(X)\) vamos a realizar lo siguiente:
aux_fun <- function(x) x * f(x) # Función auxiliar para aplicar definición
integrate(f=aux_fun, lower=12.5, upper=Inf)## 12.55 with absolute error < 1.3e-07Para obtener \(Var(X)\) vamos a realizar lo siguiente:
aux_fun <- function(x) (x-12.55)^2 * f(x) # Función auxiliar para aplicar definición
integrate(f=aux_fun, lower=12.5, upper=Inf)## 0.0025 with absolute error < 4.1e-0816.4 App shiny pdf
En el enlace que se muestra abajo hay una aplicación llamada pdf que recibe un función de densidad de probabilidad y ella entrega el dibujo de \(f(x)\), \(F(x)\), \(E(X)\) y \(Var(X)\). Para usar la aplicación usted debe copiar el siguiente código en la consola de R y esperar unos segundos para ejecutar la aplicación.