26 Distribuciones empíricas
En este capítulo se muestra la forma de crear distribuciones empíricas a partir de datos observados.
26.1 Una variable
Las funciones para obtener la densidad empírica \(f_n(x)\) y la función de distribución acumulada empírica \(F_n(x)\) de una variable cuantitativa son density y ecdf del paquete básico stats. A continuación al estructura de las funciones.
density(x, bw = "nrd0", adjust = 1,
kernel = c("gaussian", "epanechnikov", "rectangular",
"triangular", "biweight",
"cosine", "optcosine"),
weights = NULL, window = kernel, width,
give.Rkern = FALSE, subdensity = FALSE,
n = 512, from, to, cut = 3, na.rm = FALSE, ...)
ecdf(x)Ejemplo
Supongamos que se obtener una distribución empírica para la variable altura de los hombres de la base de datos medidas del cuerpo.
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)Solución
Ahora vamos a dibujar \(f_n(x)\) y \(F_n(x)\).
par(mfrow=c(1, 2))
plot(emp_f, las=1, main="Empirical fn(x)", xlab="Altura", ylab="fn(x)")
plot(emp_F, las=1, main="Empirical Fn(x)", xlab="Altura")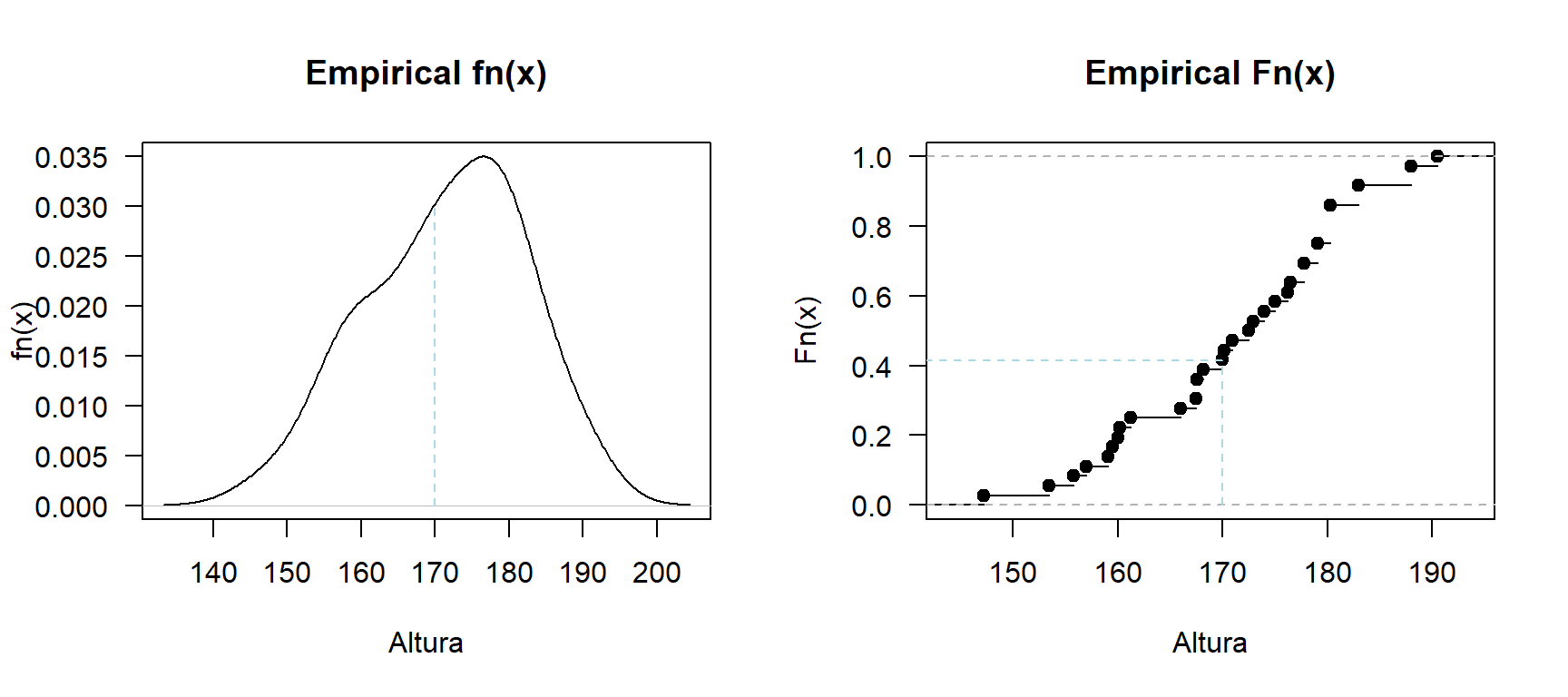
Figure 26.1: fn(x) y Fn(x) para las alturas.
¿Cuál será el valor de \(P(Altura \leq 170)\)?
Para responder esta pregunta podemos hacerlo de varias maneras:
- Observando la figura de \(f_n(x)\). Al subir desde Altura = 170 chocamos con la curva y calculamos el área bajo la curva y a la izquierda de 170.
- Observando la figura de \(F_n(x)\). Al subir desde Altura = 170 chocamos con la curva a una altura aproximada de 0.41.
- Evaluando 170 en la función
emp_Fasí:
## [1] 0.4166667De ambas formas se llega a que \(P(Altura \leq 170) = 0.4166\).