22 Selección de la distribución

En este capítulo se mostrará cómo usar R para obtener obtener el listado de las distribuciones que mejor explican una variable.

22.1 Función fitDists

La función fitDist del paquete gamlss permite explorar las distribuciones que mejor explican un conjunto de datos.

La función fitDist tiene la siguiente estructura:

fitDist(y, k = 2, 
        type = c("realAll", "realline", "realplus",
                 "real0to1", "counts", "binom")
        )

El parámetro y sirve para ingresar el vector con la información; k=2 es la penalización por cada parámetro estimado para calcular el criterio de información de Akaike Generalizado (\(GAIC\)), y el parámetro type sirve para indicar el tipo de distribución, los posibles valores son:

  • realAll: para hacer la búsqueda en todas las distribuciones disponibles en gamlss.
  • realline: para variables en \(\Re\).
  • realplus: para variables en \(\Re^+\).
  • real0to1: para variables en el intervalo \((0, 1)\).
  • counts: para variables de conteo.
  • binom: para variables de tipo binomial.
El \(GAIC\) se define como \(GAIC=-2 \times loglik + k \times \#param\), cuando el valor de penalización es \(k=2\), el \(GAIC\) se llama \(AIC\).

Ejemplo

Generar \(n=500\) observaciones de una gamma con parámetro \(\mu=2\) y parámetro \(\sigma=0.5\) y verificar si la función fitDist logra identificar que los datos fueron generados de una distribución gamma. Use \(k=2\) para calcular el \(AIC\).

Solución

Para generar la muestra aleatoria solicitada se fijó la semilla con el objetivo de que el lector pueda obtener los mismos resultados de este ejemplo. En este ejemplo vamos a usar la función rGA del paquete gamlss para simular la muestra aleatoria ma.

library(gamlss)
n <- 500
set.seed(12345)
ma <- rGA(n=n, mu=2, sigma=0.5)

Para ver los datos simulados vamos a construir un histograma sencillo y en el eje horizontal se van a destacar los datos usando una especie de “tapete” con la función rug.

hist(x=ma, freq=FALSE, main="")
rug(x=ma, col="deepskyblue3")
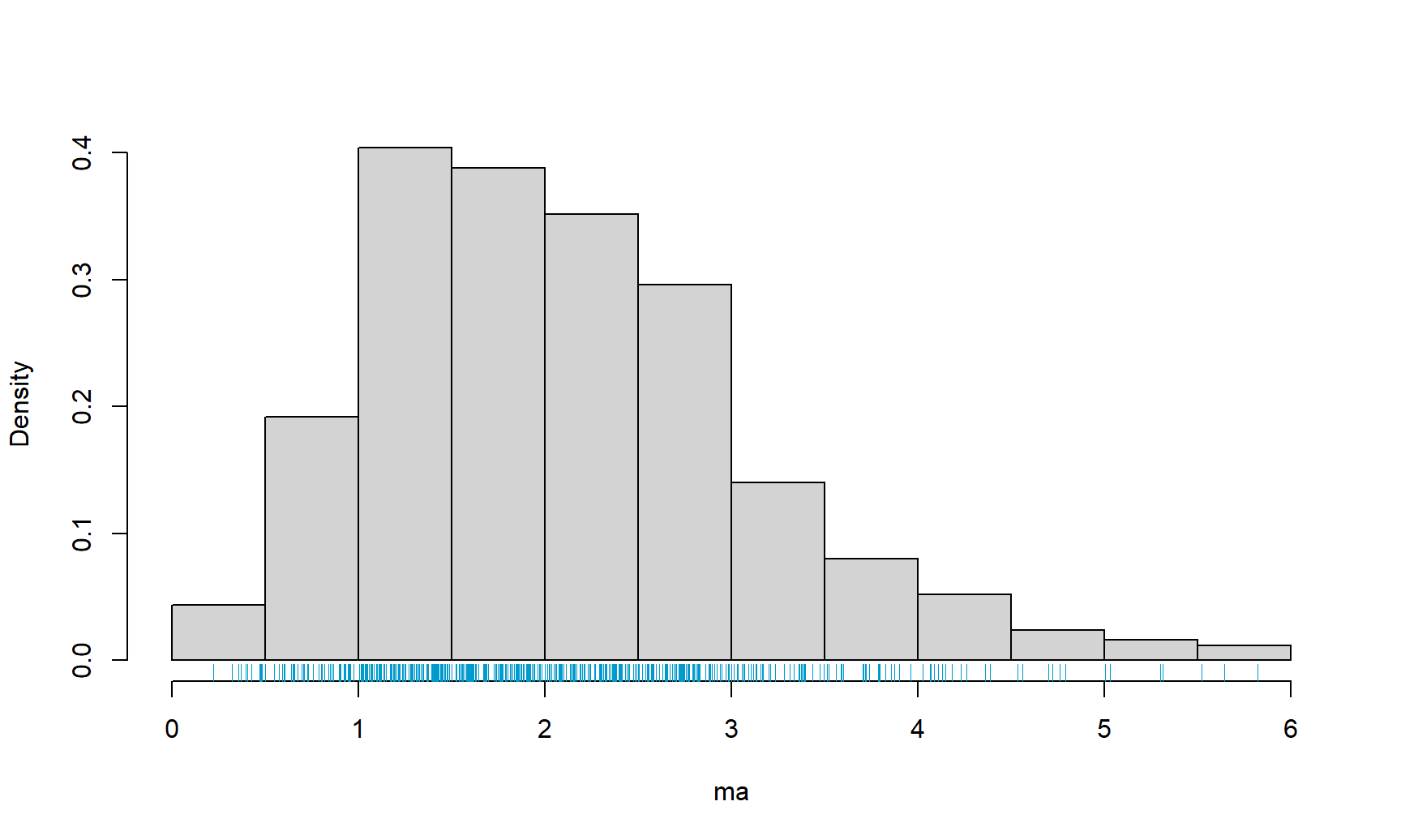
Histograma para la muestra simulada con la densidad de una Gamma(mu=4.308, sigma=0.6682).

Figure 22.1: Histograma para la muestra simulada con la densidad de una Gamma(mu=4.308, sigma=0.6682).

Se va a usar la función fitDist con type='realplus' porque se sabemos que la muestra aleatoria tiene valores en \(\Re^+\). Los resultados de almacenan en el objeto modelos y para obtener la lista de los mejores modelos con su respectivo \(AIC\) se escribe en la consola modelos$fits. Abajo el código usado.

modelos <- fitDist(y=ma, type='realplus')
##   |                                                                              |                                                                      |   0%  |                                                                              |===                                                                   |   4%  |                                                                              |======                                                                |   9%  |                                                                              |=========                                                             |  13%  |                                                                              |============                                                          |  17%  |                                                                              |===============                                                       |  22%  |                                                                              |==================                                                    |  26%  |                                                                              |=====================                                                 |  30%  |                                                                              |========================                                              |  35%  |                                                                              |===========================                                           |  39%  |                                                                              |==============================                                        |  43%
##   |                                                                              |=================================                                     |  48%
##   |                                                                              |=====================================                                 |  52%
##   |                                                                              |========================================                              |  57%  |                                                                              |===========================================                           |  61%  |                                                                              |==============================================                        |  65%  |                                                                              |=================================================                     |  70%  |                                                                              |====================================================                  |  74%  |                                                                              |=======================================================               |  78%  |                                                                              |==========================================================            |  83%Error in solve.default(oout$hessian) : 
##   Lapack routine dgesv: system is exactly singular: U[4,4] = 0
##   |                                                                              |=============================================================         |  87%
##   |                                                                              |================================================================      |  91%  |                                                                              |===================================================================   |  96%  |                                                                              |======================================================================| 100%
modelos$fits
##       GA       GG    BCCGo     BCCG      GIG      GB2    BCPEo     BCPE 
## 1368.503 1368.561 1369.284 1369.284 1370.503 1370.562 1370.967 1370.967 
##     BCTo      BCT      WEI     WEI2     WEI3   exGAUS    LOGNO   LOGNO2 
## 1371.284 1371.284 1376.365 1376.365 1376.365 1383.357 1401.925 1401.925 
##       IG   IGAMMA      EXP       GP  PARETO2 PARETO2o 
## 1418.277 1488.333 1738.337 1740.337 1740.337 1740.338

De la lista anterior se observa que la función gamma está en el primer lugar con el menor valor de \(AIC=1368.5027744\). Esto significa que la distribución gamma explica mejor los datos de la muestra, y esto coincide con la realidad, ya que la muestra fue generada de una distribución gamma.

En la salida anterior se observan unos mensajes de error que no deben causar preocupación. Esos errores se deben al proceso de estimación de parámetros con algunas de las distribuciones que no aparecen en la lista final.

Para obtener los valores estimados de \(\mu\) y \(\sigma\) se usa el siguiente código.

modelos$mu
## [1] 2.088272
modelos$sigma
## [1] 0.4945352

De esta última salida tenemos que \(\hat{\mu}=2.09\) y \(\hat{\sigma}=0.49\), mientras que los verdaderos valores eran \(\mu=2\) y \(\sigma=0.5\), esto significa que la función fitDists logró identificar correctamente la distribución y los parámetros de la distribución.

Por último vamos a dibujar el histograma para la muestra aleatoria y vamos a agregar la densidad de la distribución gamma identificada como la distribución que mejor explica el comportamiento de la variable. Para hacer lo deseado se usa la función histDist del paquete gamlss, sólo es necesario ingresar los datos y el nombre de la distribución. Abajo el código usado.

h <- histDist(y=ma, family=GA, main='', xlab='x', ylab='Densidad',
              line.col='deepskyblue3', line.wd=4, ylim=c(0, 0.45))
rug(x=ma, col="deepskyblue3")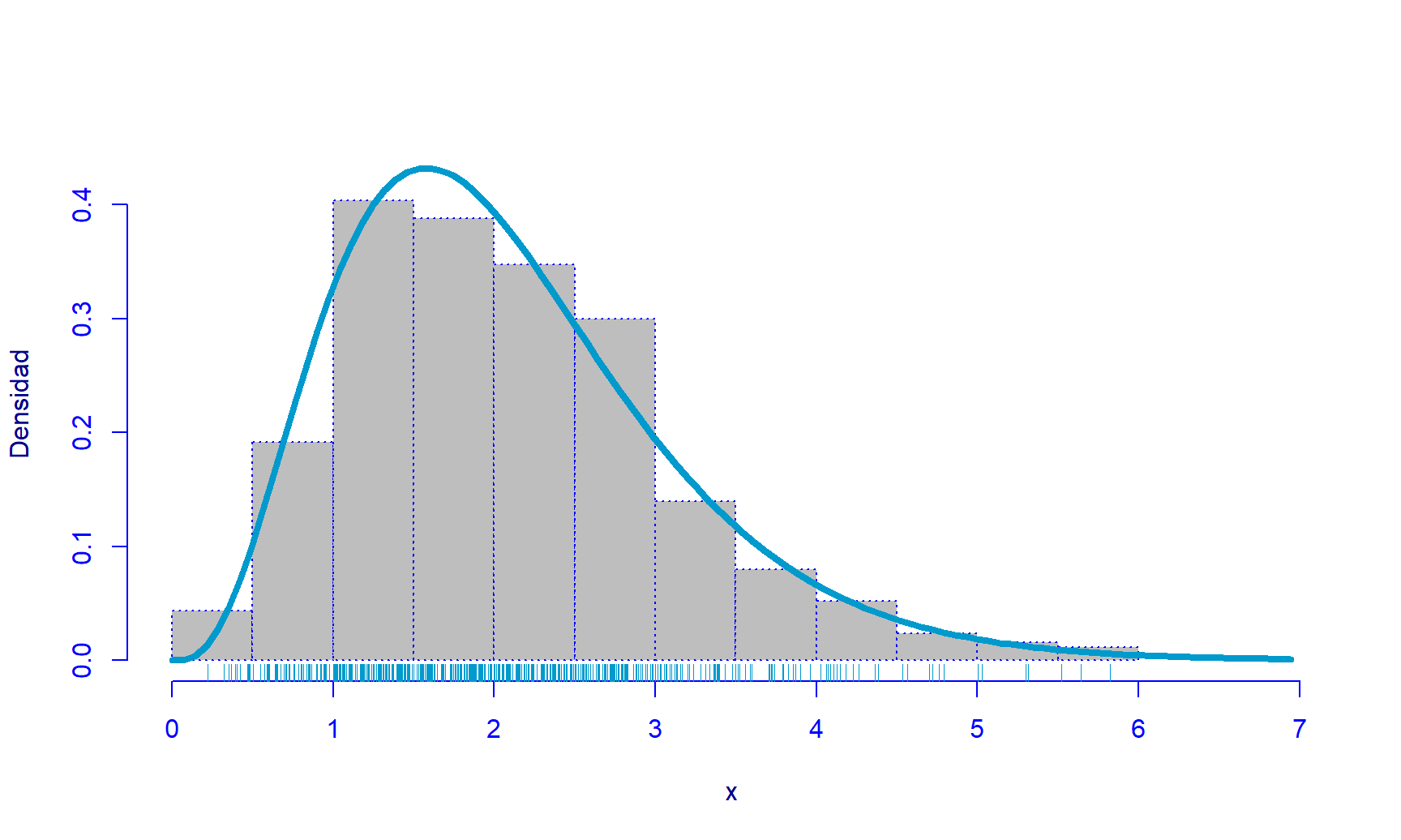
Histograma para la muestra simulada con la densidad de una Gamma(mu=2.09, sigma=0.49).

Figure 22.2: Histograma para la muestra simulada con la densidad de una Gamma(mu=2.09, sigma=0.49).

En la Figura 22.2 se presenta el histograma para muestra aleatoria y la densidad de la gamma que mejor explica estos datos. Se observa claramente que la curva de densidad azul acompaña la forma del histograma.

22.2 ¿Qué tipo de preguntas se podrían responder luego?

Una vez que tenemos identificada la distribución que mejor explica una variable \(X\) y los valores de sus parámetros, podemos hacernos preguntas como las siguientes:

  • ¿Cuál podría ser el promedio de la variable \(X\)?.
  • ¿Cuál será la varianza de la variable \(X\)?
  • ¿\(P(X < 4.5)\)?
  • ¿Cuál será el valor de \(a\) para que \(P(X<a)=0.74\)?

¿Cómo se resuelven estas preguntas con R? En el siguiente ejemplo lo vamos a mostrar.

Ejemplo

Usando la distribución y los parámetros estimados (\(Gamma(\mu=2.09, \sigma=0.49)\)) del ejemplo incial, responder las preguntas anteriores.

Solución

  • ¿Cuál podría ser el promedio de la variable \(X\)?.

El valor promedio o valor esperado de una variable continua se define como \(E(X) = \int_{-\infty}^{\infty} x f(x) dx\), siendo \(f(x)\) la función de densidad.

Para calcular el valor promedio de de \(X\) asumiendo una distribución \(Gamma(\mu=2.09, \sigma=0.49)\) hacemos lo siguiente:

fun1 <- function(x, mu, sigma) x * dGA(x=x, mu=2.09, sigma=0.49)

integrate(f=fun1, 
          lower=0, upper=Inf,
          mu=2.09, sigma=0.49)
## 2.09 with absolute error < 3.8e-06

El resultado anterior nos indica que el valor promedio o esperado de \(X\) es 2.09 aproximadamente.

  • ¿Cuál será la varianza de la variable \(X\)?

El valor promedio o valor esperado de una variable continua se define como \(Var(X) = \int_{-\infty}^{\infty} (x-E(X))^2 f(x) dx\), siendo \(f(x)\) la función de densidad.

Para calcular la varianza hacemos lo siguiente:

fun2 <- function(x, mu, sigma) (x-2.09)^2 * dGA(x=x, mu=2.09, sigma=0.49)

integrate(f=fun2, 
          lower=0, upper=Inf,
          mu=2.09, sigma=0.49)
## 1.048781 with absolute error < 2.2e-05

El resultado anterior nos indica que la varianza de \(X\) es 1.05 aproximadamente.

  • ¿\(P(X < 4.5)\)?

Para responder esto se hace lo siguiente.

pGA(q=4.5, lower.tail=TRUE, mu=2.09, sigma=0.49)
## [1] 0.9741776
  • ¿Cuál será el valor de \(a\) para que \(P(X<a)=0.74\)?

Para responder esto se hace lo siguiente.

qGA(p=0.74, lower.tail=TRUE, mu=2.09, sigma=0.49)
## [1] 2.623601

En la figura siguiente volvemos a dibujar la densidad \(Gamma(\mu=2.09, \sigma=0.49)\) para que visualmente podamos interpretar los resultados anteriores. La figura está acompañada de tres líneas de colores que representan las respuestas anteriores.

curve(dGA(x, mu=2.09, sigma=0.49),
      ylab='Densidad', col='deepskyblue3', lwd=4, las=1, 
      xlim=c(0, 7), ylim=c(0, 0.45))
grid()
abline(v=2.09, col="orange", lty="dashed")
abline(v=4.5, col="blue", lty="dashed")
abline(v=2.62, col="red", lty="dashed")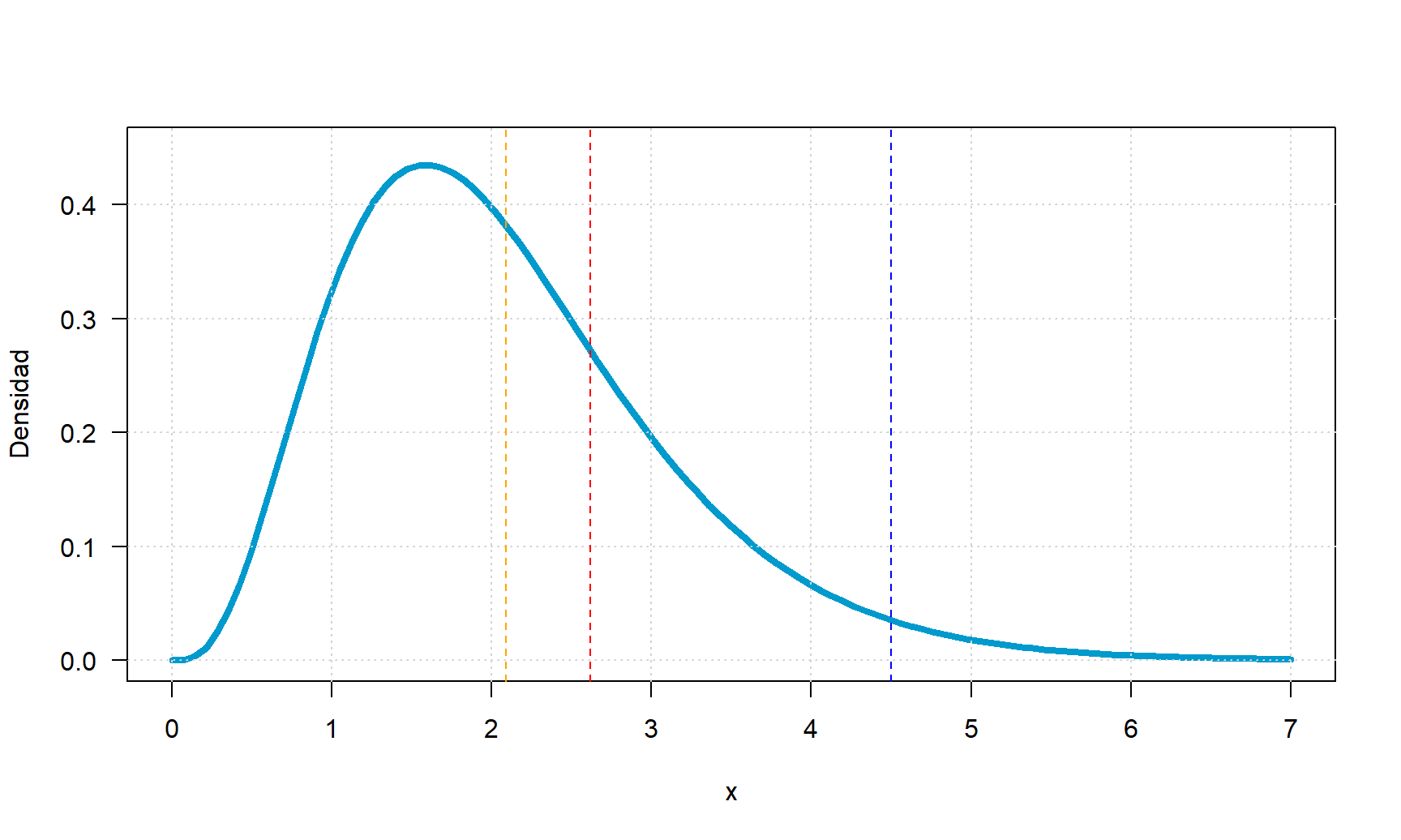
Densidad de una Gamma(mu=2.09, sigma=0.49).

Figure 22.3: Densidad de una Gamma(mu=2.09, sigma=0.49).

Cuando la distribución es discreta el \(E(X)\) se calcula como una sumatoria, es decir, \(E(X) = \sum_{-\infty}^{\infty} x f(x) dx\).

EJERCICIOS

  1. Simule 500 observaciones de la distribución discreta Poisson \(PO(\mu=7.4)\) y luego use la función fitDists para identificar la distribución y estimar el parámetro de la distribución.

  2. Usando los resultados anteriores responda las siguientes preguntas.

  • ¿Cuál podría ser el promedio de la variable \(X\)?.
  • ¿Cuál será la varianza de la variable \(X\)?
  • ¿\(P(X \geq 5)\)?
  • ¿Cuál será el valor de \(a\) para que \(P(X \geq a)=0.74\)?

  1. En este enlace hay una aplicación Shiny llamada Bondad de ajuste que se puede utilizar para identificar la mejor distribución utilizando un archivo externo con datos. Explore la aplicación y úsela.

  2. En este ejercicio usted debe evaluar qué tan bien la función fitDists identifica la distribución correcta a partir de una muestra aleatoria de tamaño \(n\). En otras palabras, para un valor \(n\) fijo, usted debe generar diez muestras de tamaño \(n\) de una población \(GA(\mu=2, \sigma=0.5)\), luego usar la función fitDists para obtener la distribución recomendad y por último contar la cantidad de aciertos y con ello el porcentaje de aciertos dividiendo por diez. Los resultados los debe consignar en la siguiente tabla.

\(n\) Número de aciertos Porcentaje acierto
5
10
20
50
100
200
500
1000

¿Logra ver algún patrón en los resultados? ¿Se debería presentar algún patrón?

  1. Repita el ejercicio anterior pero cambiando el número de repeticiones de diez a cien. No lo haga manualmente, use una instrucción for algo similar para automatizar el proceso.