20 Estudiando la normalidad

En este capítulo se mostrará cómo utilizar las herramientas de R para estudiar la normalidad univariada de un conjunto de datos.

20.1 Consideraciones iniciales

En estadística hay una gran cantidad de modelos, pruebas y procedimientos que tienen como supuesto la normalidad, por lo tanto, se hace necesario contar con herramientas que nos guíen para responder si se cumple o no el supuesto de normalidad.

Para estudiar si una muestra aleatoria proviene de una población con distribución normal se disponen de tres herramientas que se listan a continuación.

Histograma y/o densidad.
Gráficos cuantil cuantil (QQplot).
Pruebas de hipótesis.

Al construir un histograma y/o densidad para la variable de interés se puede evaluar visualmente la simetría de la distribución de los datos. Si se observa una violación clara de la simetría (sesgo a uno de los lados) o si se observa una distribución con más de una moda, eso sería indicio de que la muestra no proviene de una población normal. Por otra parte, si se observa simetría en los datos, esto NO garantiza que la muestra aleatoria proviene de una población normal y se hace necesario recurrir a otras herramientas específicas para estudiar normalidad como lo son los gráficos QQplot y pruebas de hipótesis.

A continuación se presentan varias secciones donde se profundiza sobre el uso de cada de las tres herramientas anteriormente listadas para estudiar la normalidad.

20.2 Histograma y densidad

El histograma y el gráfico de densidad son herramientas muy útiles porque sirven para mostrar la distribución, la simetría, el sesgo, variabilidad, moda, mediana y observaciones atípicas de un conjunto de datos. Para explorar la normalidad de un conjunto de datos lo que se busca es que el histograma o gráfico de densidad presenten un patrón más o menos simétrico. Para obtener detalles de la construcción de histogramas y gráficos de densidad se recomienda consultar Hernández (2018).

A continuación se presentan dos ejemplos, uno con datos simulados y otro con datos reales, con los cuales se muestra la utilidad del histograma y gráfico de densidad al explorar la normalidad.

Ejemplo densidad con datos simulados

Simular 4 muestra aleatorias de una \(N(0, 1)\) con tamaños de muestra \(n\)=10, 100, 1000 y 10000; para cada una de las muestras construir los gráficos de densidad y analizar si son simétricos.

Lo primero que se debe hacer es definir el vector n con los valores de los tamaños de muestra, luego dentro de una sentencia for se simula cada muestra y se dibuja su densidad.

par(mfrow=c(2, 2))
n <- c(10, 100, 1000, 10000)
for (i in n) {
  x <- rnorm(i)
  plot(density(x), main=bquote(~ n == .(i)),
       ylab='Densidad', col='blue3', xlab='x', las=1, lwd=4)
}

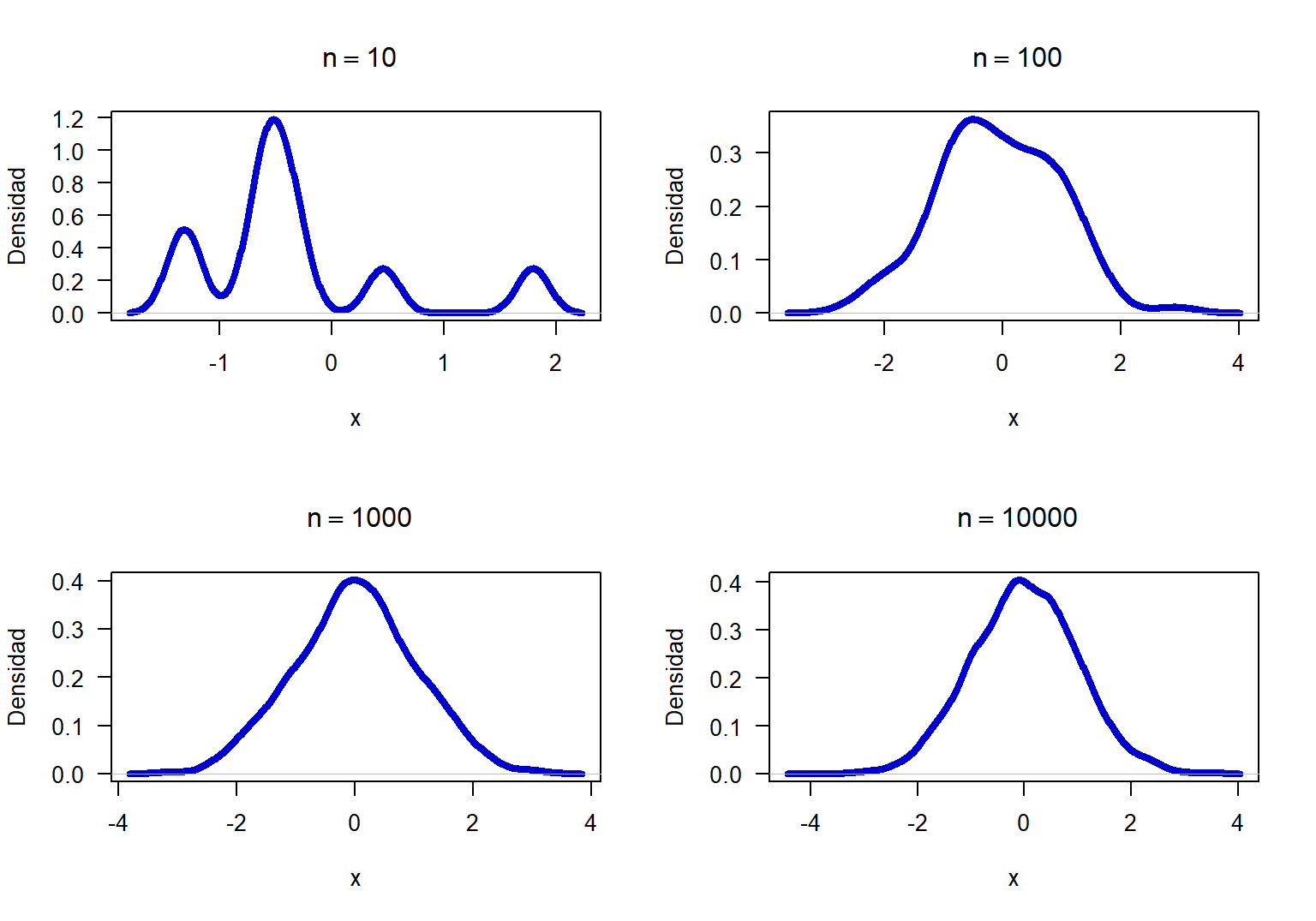
Figure 20.1: Densidad para 4 muestras de una N(0, 1) con diferente tamaño de muestra.

En la Figura 20.1 se muestran las cuatro densidades, de esta figura se observa que, a pesar de haber generado las muestras de una normal estándar, las densidades no son perfectamente simétricas, sólo para el caso de tamaño de muestra \(n=10000\) la densidad muestral fue bastante simétrica. Esto significa que el gráfico de densidad se debe usar con precaución para decidir sobre la normalidad de un conjunto de datos, como regla práctica se aconseja lo siguiente:

Si la densidad muestral es muy pero muy asimétrica se debe desconfiar de la normalidad de los datos.
Si la densidad muestral es más o menos simétrica, se deben usar otras herramientas como QQplot o pruebas de hipótesis para obtener una mejor conclusión.

Si un histograma o densidad es muy asimétrico o sesgado, es evidencia en contra de la normalidad de los datos. Si el histograma o densidad presentan simetría, esto no es garantía de la normalidad de los datos.

Ejemplo densidad del peso corporal

Considerando la base de datos medidas del cuerpo presentada en el Capítulo 11, se desea saber si el peso corporal, tanto de hombres y mujeres, tiene una distribución normal.

Para hacer la exploración lo primero es cargar la base de datos usando el siguiente código.

url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)

La variable peso del objeto datos contiene la información sobre el peso corporal de ambos sexos, debemos entonces partir o dividir esta información diferenciando entre hombres y mujeres, para esto usamos la función split de la siguiente forma.

pesos <- split(datos$peso, datos$sexo)
pesos  # Para ver los elementos de la lista pesos

## $Hombre
##  [1] 87.3 80.0 82.3 73.6 74.1 85.9 73.2 76.3 65.9 90.9 89.1 62.3 82.7 79.1 98.2
## [16] 84.1 83.2 83.2
## 
## $Mujer
##  [1] 51.6 59.0 49.2 63.0 53.6 59.0 47.6 69.8 66.8 75.2 55.2 54.2 62.5 42.0 50.0
## [16] 49.8 49.2 73.2

El objeto pesos es una lista con dos elementos, el primero contiene los pesos de los hombres mientras que el segundo contiene los pesos de las mujeres. Note que pesos es un objeto mientras que peso es el nombre usado para la variable peso corporal en la base de datos.

Para explorar la normalidad de los pesos se dibujan dos densidades, una para el peso de hombres y otra para el peso de las mujeres, a continuación el código utilizado.

plot(density(pesos$Hombre), lwd=3, col='blue',
     xlim=c(30, 110), main='', las=1,
     xlab='Peso (kg)', ylab='Densidad')
lines(density(pesos$Mujer), lwd=3, col='deeppink')
legend('topleft', legend=c('Hombres', 'Mujeres'),
       lwd=3, col=c('blue', 'deeppink'), bty='n')

Figure 20.2: Densidad para el peso corporal de hombres y mujeres.

En la Figura 20.2 se muestran las dos densidades, en la figura no se observa una evidencia clara de sesgo, lo que se observa es que la densidad para los hombres es un poco más simétrica que la densidad para las mujeres. De estos resultados no se puede rechazar la premisa de que pesos corporales provienen de una distribución normal, lo recomendable es construir QQplot y aplicar prueba de hipótesis.

20.3 Gráficos cuantil cuantil

Los gráficos cuantil cuantil (QQplot) son una herramienta gráfica para explorar si un conjunto de datos o muestra proviene de una población con cierta distribución, en particular aquí nos interesan para estudiar la normalidad de un conjunto de datos. La función qqnorm sirve para construir el QQplot y la función qqline agrega una línea de referencia que ayuda a interpretar el gráfico QQplot, para obtener una explicación de cómo construir este gráfico se recomienda ver el video disponible en este enlace.

En la Figura 20.3 se muestra un ejemplo de un QQplot y de sus partes, los puntos y la línea de referencia. Si se tuviese una muestra distribuída perfectamente normal, se esperaría que los puntos estuviesen perfectamente alineados con la línea de referencia, sin embargo, las muestran con las que se trabajan en la práctica casi nunca presentan este comportamiento aún si fueron obtenidas de una población normal. En la práctica se aceptan alejamientos del patrón lineal para aceptar que los datos si provienen de una población normal.

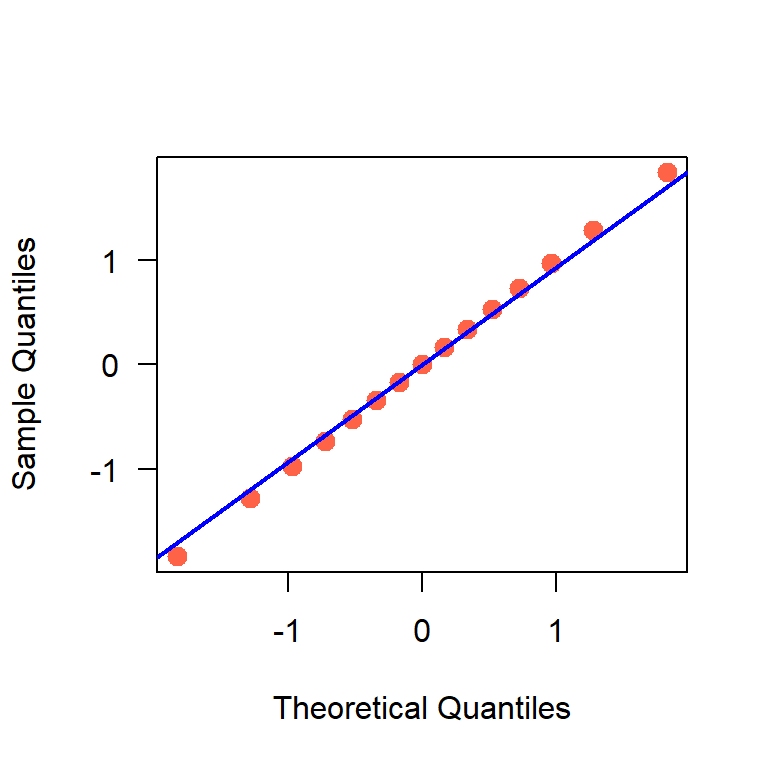
Figure 20.3: Ejemplo de un QQplot.

A continuación se presentan cuatro ejemplos, dos con datos simulados y otro con datos reales para mostrar la utilidad del qqplot al explorar la normalidad.

Ejemplo 1 QQplot con datos simulados

Simular 4 muestra aleatorias de una \(N(0, 1)\) con tamaños de muestra \(n\)=10, 30, 50 y 100, para cada una de ellas construir el QQplot.

Lo primero que se debe hacer es definir el vector n con los valores del tamaño de muestra, luego dentro de una sentencia for se simula cada muestra x y por último se dibuja el QQplot para cada muestra, a continuación el código utilizado.

par(mfrow=c(2, 2))
n <- c(10, 30, 50, 100)
for (i in n) {
  x <- rnorm(i)
  qqnorm(x, main=bquote(~ n == .(i)))
  qqline(x)  # Para agregar la linea de referencia
}

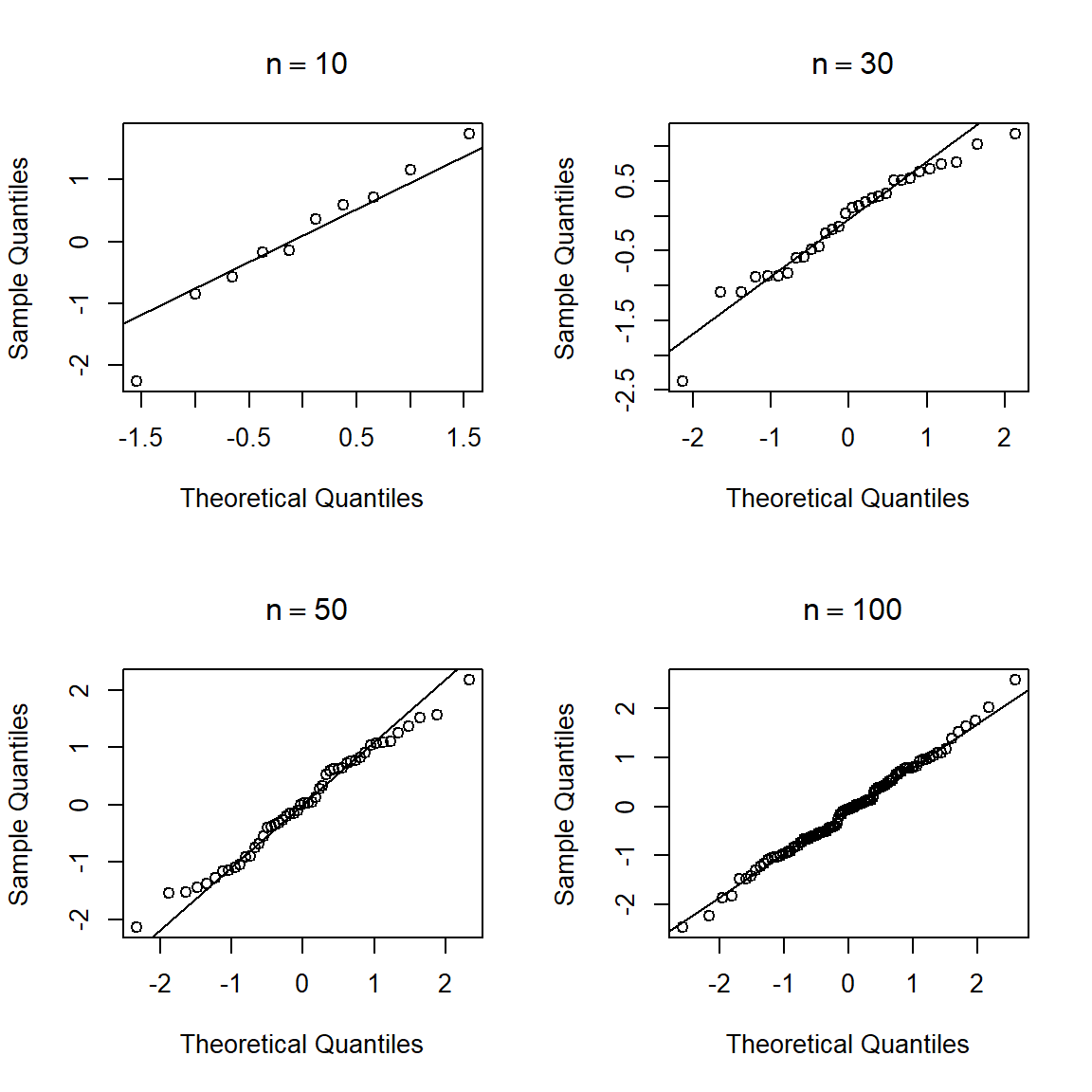
Figure 20.4: QQplot para 4 muestras de una N(0, 1) con diferente tamaño de muestra.

La Figura 20.4 muestra que, a pesar de haber simulado cada muestra x de una \(N(0, 1)\), los puntos no se alinean de forma perfecta, esto significa que en la práctica se debe ser prudente con la interpretación de un QQplot, un alejamiento del patrón lineal NO significa que la muestra no provenga de una población normal.

Ejemplo 2 QQplot con datos simulados

Simular 1 muestra aleatoria con \(n=50\) de cada una de las siguientes poblaciones Poisson(5), NBinom(5, 0.5), Gamma(2, 3) y Weibull(1, 3), para cada una de las muestras construir el QQplot para explorar la normalidad de las muestras.

Las muestras de cada una de las poblaciones se generan con las funciones rpois, rnbinom, rgamma y rweibull especificando los parámetros. A continuación el código necesario para obtener los QQplot solicitados.

m1 <- rpois(n=50, lambda=5)
m2 <- rnbinom(n=50, size=5, prob=0.35)
m3 <- rgamma(n=50, shape=2, scale=3)
m4 <- rweibull(n=50, shape=1, scale=3)
par(mfrow=c(2, 2))
qqnorm(m1, main='Poisson(5)')
qqline(m1)
qqnorm(m2, main='NBinom(5, 0.35)')
qqline(m1)
qqnorm(m3, main='Gamma(2, 3)')
qqline(m1)
qqnorm(m4, main='Weibull(1, 3)')
qqline(m1)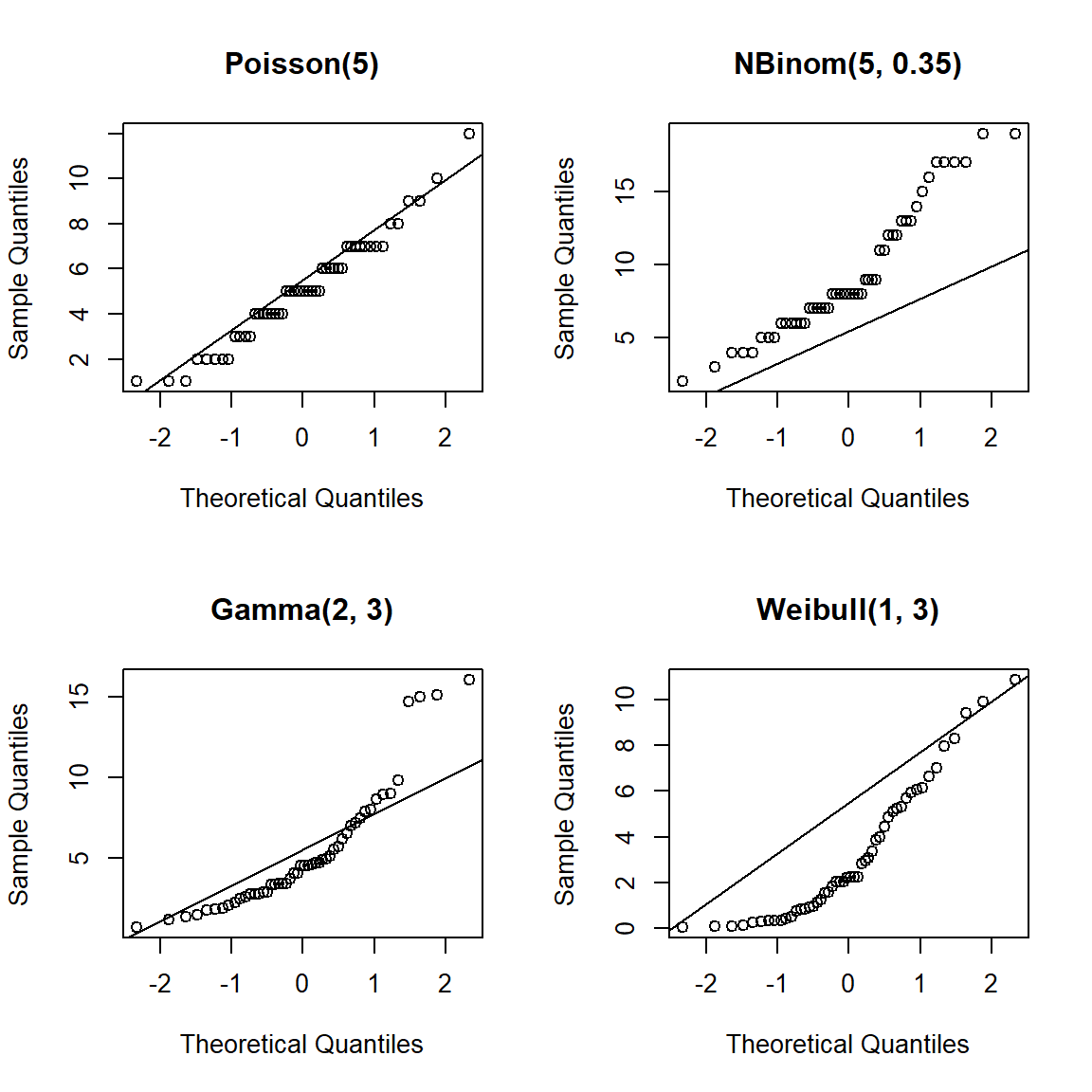

Figure 20.5: QQplot para muestras generadas de poblaciones Poisson, Binomial Negativa, Gamma y Weibull.

En la Figura 20.5 se muestran los cuatro QQplot para cada una de las muestras generadas de las distribuciones indicadas. Se observa claramente que los puntos del QQplot no está alineados, esto es una clara evidencia de que las muestras NO provienen de poblaciones normales. Otro aspecto interesante a resaltar es el patrón de escalera que se observa para las muestras generadas de poblaciones discretas (Poisson y Binomial Negativa).

Se debe tener cuidado al concluir con un QQplot, lo que para una persona puede estar alineado, para otra puede no estarlo. El QQplot es un gráfico exploratorio de normalidad.

Ejemplo QQplot para peso corporal

Retomando la base de datos medidas del cuerpo presentada en el Capítulo 11, se desea saber si el peso corporal, tanto de hombres y mujeres, tiene una distribución normal usando QQplots.

Para hacer la exploración lo primero es cargar la base de datos si aún no se ha cargado.

url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)

pesos <- split(datos$peso, datos$sexo)
pesos

## $Hombre
##  [1] 87.3 80.0 82.3 73.6 74.1 85.9 73.2 76.3 65.9 90.9 89.1 62.3 82.7 79.1 98.2
## [16] 84.1 83.2 83.2
## 
## $Mujer
##  [1] 51.6 59.0 49.2 63.0 53.6 59.0 47.6 69.8 66.8 75.2 55.2 54.2 62.5 42.0 50.0
## [16] 49.8 49.2 73.2

Para explorar la normalidad de los pesos se dibujan dos densidades, una para el peso de hombres y otra para el peso de las mujeres, a continuación el código utilizado.

par(mfrow=c(1, 2))
qqnorm(pesos$Hombre, pch=20,
       main='QQplot para peso de hombres')
qqline(pesos$Hombre)

qqnorm(pesos$Mujer, pch=20,
       main='QQplot para peso de mujeres')
qqline(pesos$Mujer)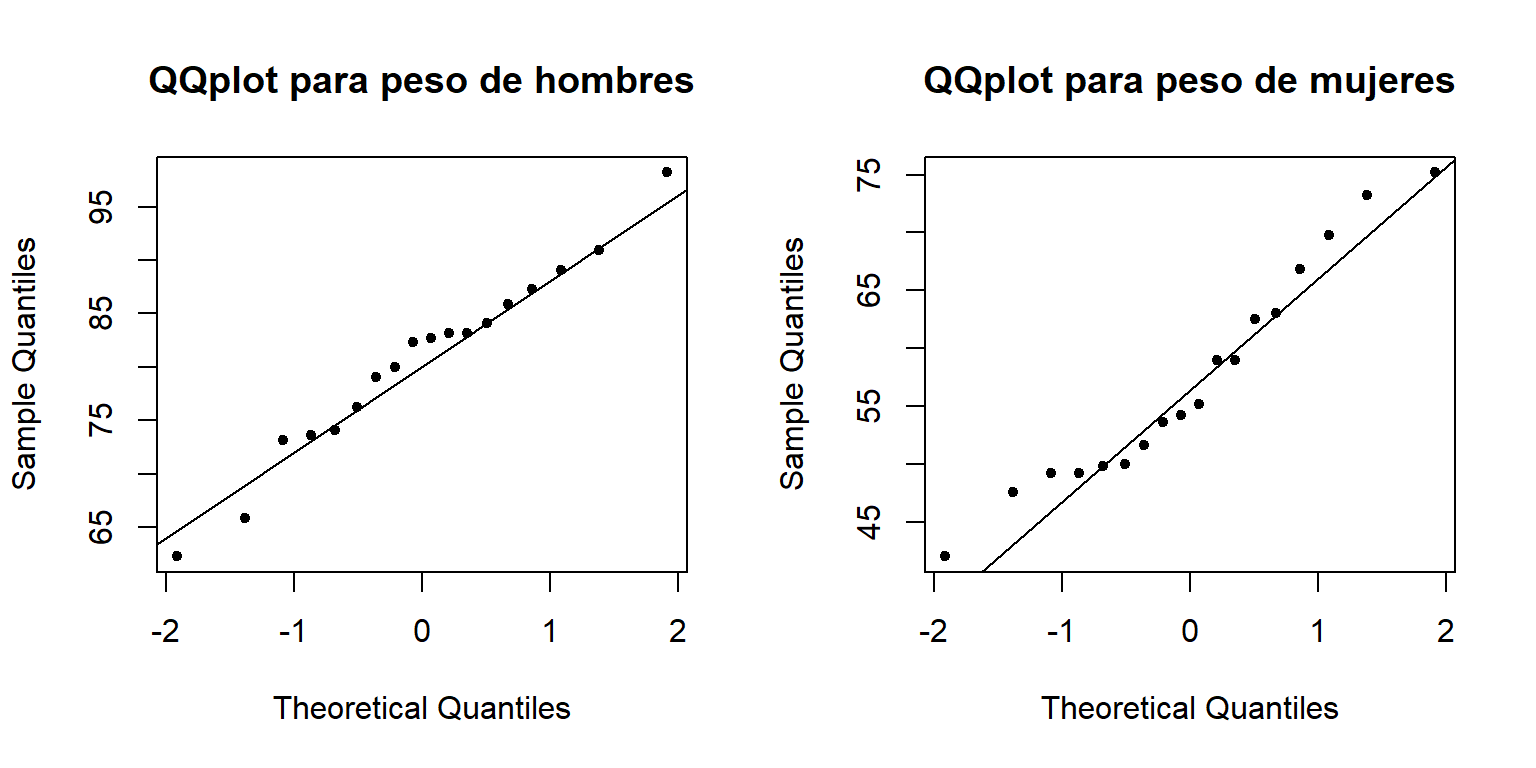

Figure 20.6: QQplot para el peso corporal de hombres y mujeres.

La Figura 20.6 muestra el QQplot para el peso corporal de hombres y mujeres, de la figura se observa que los puntos no están tan desalineados, lo cual cual nos lleva a no rechazar la hipótesis de normalidad.

Se debe interpretar con precaución el QQplot, del ejemplo con datos simulados se vió que a pesar de haber generado las muestras de una \(N(0,1)\) los QQplot no siempre están perfectamente alineados.

Ejemplo QQplot con bandas

Construir QQplot con bandas de confianza para el peso corporal de hombres y mujeres con los datos del ejemplo anterior. ¿Se puede afirma que los pesos corporales provienen de una distribución normal?

Para construir este tipo de QQplot se usa la función qqplot del paquete car. A continuación el código para construir el gráfico solicitado.

require(car)
par(mfrow=c(1, 2))
qqPlot(pesos$Hombre, pch=20, ylab='Peso (Kg)',
       main='QQplot para peso de hombres')

## [1] 12 15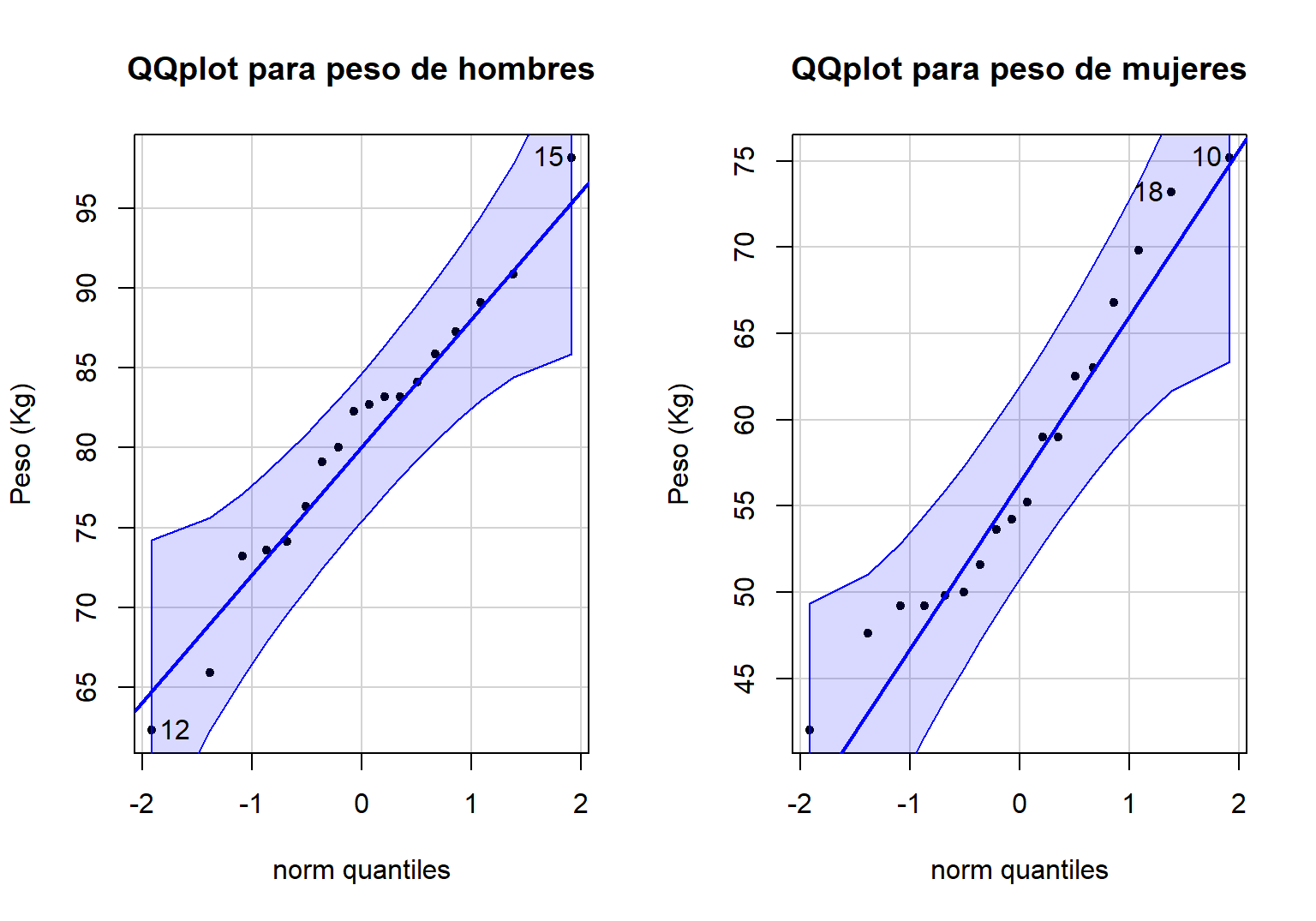

qqPlot(pesos$Mujer, pch=20, ylab='Peso (Kg)',
       main='QQplot para peso de mujeres')

Figure 20.7: QQplot con bandas de confianza para el peso corporal de hombres y mujeres.

## [1] 10 18

En la Figura 20.7 se muestra el QQplot solicitado, como los puntos del QQplot están dentro de las bandas se puede aceptar que los pesos corporales provienen de una población normal.

La función qqPlot tiene varios parámetros adicionales que recomendamos consultar en la ayuda de la función help(qqPlot).

20.4 Pruebas de normalidad

Una forma menos subjetiva de explorar la normalidad de un conjunto de datos es por medio de las pruebas de normalidad. Las hipótesis para este tipo de pruebas son:

\[\begin{equation} \begin{split} &H_0: \text{la muestra proviene de una población normal.} \\ &H_A: \text{la muestra NO proviene de una población normal.} \end{split} \end{equation}\]

En la literatura estadística se reportan varias pruebas, algunas de ellas se listan a continuación.

Prueba Shapiro-Wilk con la función shapiro.test.
Prueba Anderson-Darling con la función ad.test del paquete nortest.
Prueba Cramer-von Mises con la función cvm.test del paquete nortest.
Prueba Lilliefors (Kolmogorov-Smirnov) con la función lillie.test del paquete nortest.
Prueba Pearson chi-square con la función pearson.test del paquete nortest.
Prueba Shapiro-Francia con la función sf.test del paquete nortest).

Ejemplo con datos simulados

Generar una muestra aleatoria con \(n=100\) de una \(N(150, 25)\) y aplicar las pruebas de normalidad Shapiro-Wilk y Anderson-Darling con un nivel de significancia del 3%.

Lo primero es generar la muestra aleatoria x así:

x <- rnorm(n=100, mean=150, sd=5)

Para aplicar la prueba Shapiro-Wilk se usa la función shapiro.test al vector x así:

shapiro.test(x)

## 
##  Shapiro-Wilk normality test
## 
## data:  x
## W = 0.99356, p-value = 0.9195

De la salida anterior se tiene que el valor-P para la prueba fue de 0.9 y que es mayor al nivel de significancia 3%, lo cual indica que no hay evidencias para rechazar la hipótesis nula de normalidad.

Para aplicar la prueba Anderson-Darling se usa la función ad.test al vector x así:

require(nortest)  # Se debe haber instalado nortest
ad.test(x)

## 
##  Anderson-Darling normality test
## 
## data:  x
## A = 0.10456, p-value = 0.9948

De la salida anterior se tiene que el valor-P para la prueba fue de 1 y que es mayor al nivel de significancia 3%, esto indica que no hay evidencias para rechazar la hipótesis nula de normalidad.

Ejemplo normalidad para peso corporal

Retomando la base de datos medidas del cuerpo presentada en el Capítulo 11, se desea saber si el peso corporal, tanto de hombres y mujeres, tiene una distribución normal usando las pruebas normalidad Shapiro-Wilks y Anderson-Darling con un nivel de significancia del 5%.

Lo primero es cargar la base de datos si aún no se ha cargado.

url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)

pesos <- split(datos$peso, datos$sexo)
pesos

## $Hombre
##  [1] 87.3 80.0 82.3 73.6 74.1 85.9 73.2 76.3 65.9 90.9 89.1 62.3 82.7 79.1 98.2
## [16] 84.1 83.2 83.2
## 
## $Mujer
##  [1] 51.6 59.0 49.2 63.0 53.6 59.0 47.6 69.8 66.8 75.2 55.2 54.2 62.5 42.0 50.0
## [16] 49.8 49.2 73.2

Para aplicar la prueba Shapiro-Wilk se usa la función shapiro.test. Como el objeto pesos es una lista se debe usar la función lapply para aplicar shapiro.test a la lista, a continuación el código usado.

lapply(pesos, shapiro.test)

## $Hombre
## 
##  Shapiro-Wilk normality test
## 
## data:  X[[i]]
## W = 0.97803, p-value = 0.9274
## 
## 
## $Mujer
## 
##  Shapiro-Wilk normality test
## 
## data:  X[[i]]
## W = 0.94709, p-value = 0.3812

De la salida anterior se observa que ambos valores-P fueron mayores al nivel de significancia 5%, por lo tanto, se puede concluir que ambas muestras provienen de poblaciones con distribución normal.

Para aplicar la prueba Anderson-Darling se usa la función ad.test del paquete nortest. Como el objeto pesos es una lista se debe usar la función lapply para aplicar ad.test a la lista, a continuación el código usado.

require(nortest) # Se debe haber instalado nortest
lapply(pesos, shapiro.test)

## $Hombre
## 
##  Shapiro-Wilk normality test
## 
## data:  X[[i]]
## W = 0.97803, p-value = 0.9274
## 
## 
## $Mujer
## 
##  Shapiro-Wilk normality test
## 
## data:  X[[i]]
## W = 0.94709, p-value = 0.3812

De la salida anterior se observa que ambos valores-P fueron mayores al nivel de significancia 5%, por lo tanto, se puede concluir que ambas muestras provienen de poblaciones con distribución normal.

Al usar las pruebas Shapiro-Wilks y Anderson-Darling se concluye que no hay evidencias para pensar que los pesos corporales de hombres y mujeres no provienen de una población normal.

EJERCICIOS

Para la base de datos medidas del cuerpo presentada en el Capítulo 11, explorar si la variable estatura, diferenciada por hombres y mujeres, tiene una distribución normal.

References

Hernández, J., F. & Correa. 2018. Gráficos Con R. Primera. Medellín, Colombia: Universidad Nacional de Colombia. https://fhernanb.github.io/Graficos-con-R/.