21 Verosimilitud

En este capítulo se mostrará como usar R para obtener la función de log-verosimilitud y estimadores por el método de máxima verosimilitud.

21.1 Función de verosimilitud

El concepto de verosimilitud fue propuesto por Fisher (1922) en el contexto de estimación de parámetros. En la Figura 21.1 se muestra una fotografía de Ronald Aylmer Fisher.

Figure 21.1: Fotografía de Ronald Aylmer Fisher (1890-1962).

La función de verosimilitud para un vector de parámetros \(\boldsymbol{\theta}\) dada una muestra aleatoria \(\boldsymbol{x}=(x_1, \ldots,x_n)^\top\) con una distribución asumida se define usualmente como:

\[\begin{equation} L(\boldsymbol{\theta} | \boldsymbol{x}) = \prod_{i=1}^{n} f(x_i | \boldsymbol{\theta}), \tag{21.1} \end{equation}\]

donde \(x_i\) representa uno de los elementos de la muestra aleatoria y \(f(\cdot)\) es la función de masa/densidad de la distribución de la cual se obtuvo \(\boldsymbol{x}\).

21.2 Función de log-verosimilitud

La función de log-verosimilitud \(l(\boldsymbol{\theta} | \boldsymbol{x})\) se define como el logaritmo de la función de verosimilitud \(L(\boldsymbol{\theta} | \boldsymbol{x})\), es decir

\[\begin{equation} l(\boldsymbol{\theta} | \boldsymbol{x}) = \log L(\boldsymbol{\theta} | \boldsymbol{x}) = \sum_{i=1}^{n} \log f(x_i | \boldsymbol{\theta}) \tag{21.2} \end{equation}\]

21.3 Método de máxima verosimilitud para estimar parámetros

El método de máxima verosimilitud se usa para estimar los parámetros de una distribución. El objetivo de este método es encontrar los valores de \(\boldsymbol{\theta}\) que maximizan a \(L(\boldsymbol{\theta} | \boldsymbol{x})\) o a \(l(\boldsymbol{\theta} | \boldsymbol{x})\), los valores encontrados se representan usualmente por \(\hat{\boldsymbol{\theta}}\).

Asumiendo un modelo estadístico parametrizado por una cantidad fija y desconocida \(\theta\), la verosimilitud \(L(\theta)\) es la probabilidad de los datos observados \(x\) como una función de \(\theta\) (Pawitan 2013). Si la variable de interés es discreta se usa la probabilidad y si es continua se usa la densidad para obtener la verosimilitud.

Ejemplo

En este ejemplo vamos a considerar la distribución binomial cuya función de masa de probabilidad está dada por:

\[f(x)=P(X=x)=\binom{n}{x} p^x (1-p)^{n-x}, \quad 0<p<1, \quad n \leq 1, 2, \ldots, \quad 0 \leq x \leq n\]

La distribución binomial anterior tiene sólo un parámetro \(p\), por lo tanto en este caso se \(\theta=p\).

Suponga que se tiene el vector rta que corresponde a una muestra aleatoria de una distribución binomial con parámetro \(n=5\) conocido.

rta <- c(2, 2, 1, 1, 1, 1, 0, 2, 1, 2,
         1, 0, 1, 2, 1, 0, 0, 2, 2, 1)

1. Calcular el valor de log-verosimilitud \(l(\theta)\) si asumiendo que \(p=0.30\) en la distribución binomial.

Para obtener el valor de \(l(\theta)\) en el punto \(p=0.30\) se aplica la definición dada en la expresión (21.2). Como el problema trata de una binomial se usa entonces la función de masa dbinom evaluada en la muestra rta, el parámetro size como es conocido se reemplaza por el valor de cinco y en el parámetro prob se cambia por 0.3. Como interesa la función de log-verosimilitud se debe incluir log=TRUE. A continuación el código necesario.

sum(dbinom(x=rta, size=5, prob=0.3, log=TRUE))

## [1] -24.55231

Por lo tanto \(l(\theta)= -24.55\)

2. Construir una función llamada ll a la cual le ingrese valores del parámetro \(p\) de la binomial y que la función entregue el valor de log-verosimilitud.

La función solicitada tiene un cuerpo igual al usado en el numeral anterior, a continuación el código necesario para crearla.

ll <- function(prob) sum(dbinom(x=rta, size=5, prob=prob, log=T))

Vamos a probar la función en dos valores arbitrarios \(p=0.15\) y \(p=0.80\) que pertenezcan al dominio del parámetro \(p\) de la distribución binomial.

ll(prob=0.15)  # Individual para p=0.15

## [1] -25.54468

ll(prob=0.80)  # Individual para p=0.80

## [1] -98.45598

El valor de log-verosimilitud para \(p=0.15\) fue de -25.54 mientras que para \(p=0.80\) fue de -98.46.

Vamos ahora a chequear si la función ll está vectorizada y para esto usamos el código mostrado a continuación y deberíamos obtener un vector con los valores c(-25.54, -98.56).

ll(prob=c(0.15, 0.80))

## [1] -57.31899

No obtuvimos el resultado esperado, eso significa que nuestra función no está vectorizada. Ese problema lo podemos solucionar así:

ll <- Vectorize(ll)
ll(prob=c(0.15, 0.80))

## [1] -25.54468 -98.45598

Vemos que ahora que cuando se ingresa un vector a la función ll se obtiene un vector.

Necesitamos que la función ll esté vectorizada para poder dibujarla y para poder optimizarla.

3. Dibujar la curva log-verosimilitud \(l(\theta)\), en el eje X debe estar el parámetro \(p\) del cual depende la función de log-verosimilitud.

En la Figura 21.2 se presenta la curva solicitada.

curve(ll, lwd=4, col='dodgerblue3',
      xlab='Probabilidad de éxito (p)', las=1,
      ylab="Loglik(p)")
grid()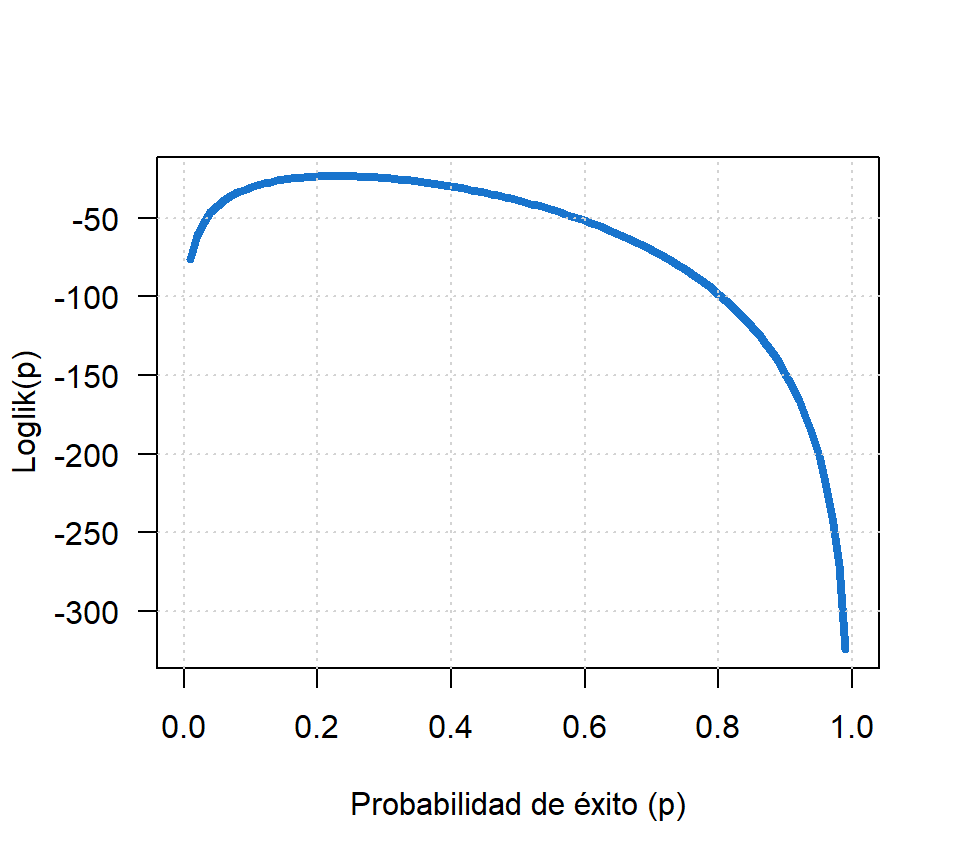

Figure 21.2: Función de log-verosimilitud para el ejemplo sobre binomial.

4. Observando la Figura 21.2, ¿cuál esl el valor de \(p\) que maximiza la función de log-verosimilitud?

Al observar la Figura 21.2 se nota que el valor de \(p\) que maximiza la función log-verosimilitud está muy cerca de 0.2.

5. ¿Cuál es el valor exacto de \(p\) que maximiza la función log-verosimilitud?

En R existe la función optimize que sirve para encontrar el valor que minimiza una función uniparamétrica en un intervalo dado, sin embargo, aquí interesa es maximimizar la función de log-verosimilitud, por esa razón se construye la función minusll que es el negativo de la función ll para así poder usar optimize. A continuación el código usado.

minusll <- function(x) -ll(x)

optimize(f=minusll, interval=c(0, 1))

## $minimum
## [1] 0.229993
## 
## $objective
## [1] 23.3246

Del resultado anterior se observa que cuando \(p=0.23\) el valor máximo de log-verosimilitud es -23.32 (negativo de minusll).

Ejemplo

Suponga que la estatura de una población se puede asumir como una normal \(N(170, 25)\). Suponga también que se genera una muestra aleatoria de 50 observaciones de la población con el objetivo de recuperar los valores de la media y varianza poblacionales a partir de la muestra aleatoria.

La muestra se va a generar con la función rnorm pero antes se fijará una semilla con la intención de que el lector pueda replicar el ejemplo y obtener la misma muestra aleatoria aquí generada, el código para hacerlo es el siguiente.

set.seed(1235)  # La semilla es 1235
y <- rnorm(n=50, mean=170, sd=5)
y[1:7]  # Para ver los primeros siete valores generados

## [1] 166.5101 163.5757 174.9498 170.5589 170.5710 178.4910 170.2392

1. Construya la función de log-verosimilitud para los parámetros de la normal dada la muestra aleatoria y.

Abajo se muestra la forma de construir la función de log-verosimilitud.

ll <- function(param) {
  media <- param[1]  # param es el vector de parámetros
  desvi <- param[2] 
  sum(dnorm(x=y, mean=media, sd=desvi, log=TRUE))
}

Siempre que el interés sea encontrar los valores que maximizan una función de log-verosimilitud, los parámetros de la distribución deben ingresar a la función ll como un vector. Esto se debe hacer para poder usar las funciones de búsqueda optim y nlminb.

2. Dibujar la función de log-verosimilitud.

En la Figura 21.3 se muestra el gráfico de niveles para la superficie de log-verosimilitud. De esta figura se nota claramente que los valores que maximizan la superficie están alrededor de \(\mu=170\) y \(\sigma=5\).

ll1 <- function(a, b) sum(dnorm(x=y, mean=a, sd=b, log=TRUE))
ll1 <- Vectorize(ll1)
xx <- seq(from=160, to=180, by=0.5)
yy <- seq(from=3, to=7, by=0.5)
zz <- outer(X=xx, Y=yy, ll1)
filled.contour(x=xx, y=yy, z=zz, nlevels=20,
               xlab=expression(mu), ylab=expression(sigma),
               color = topo.colors)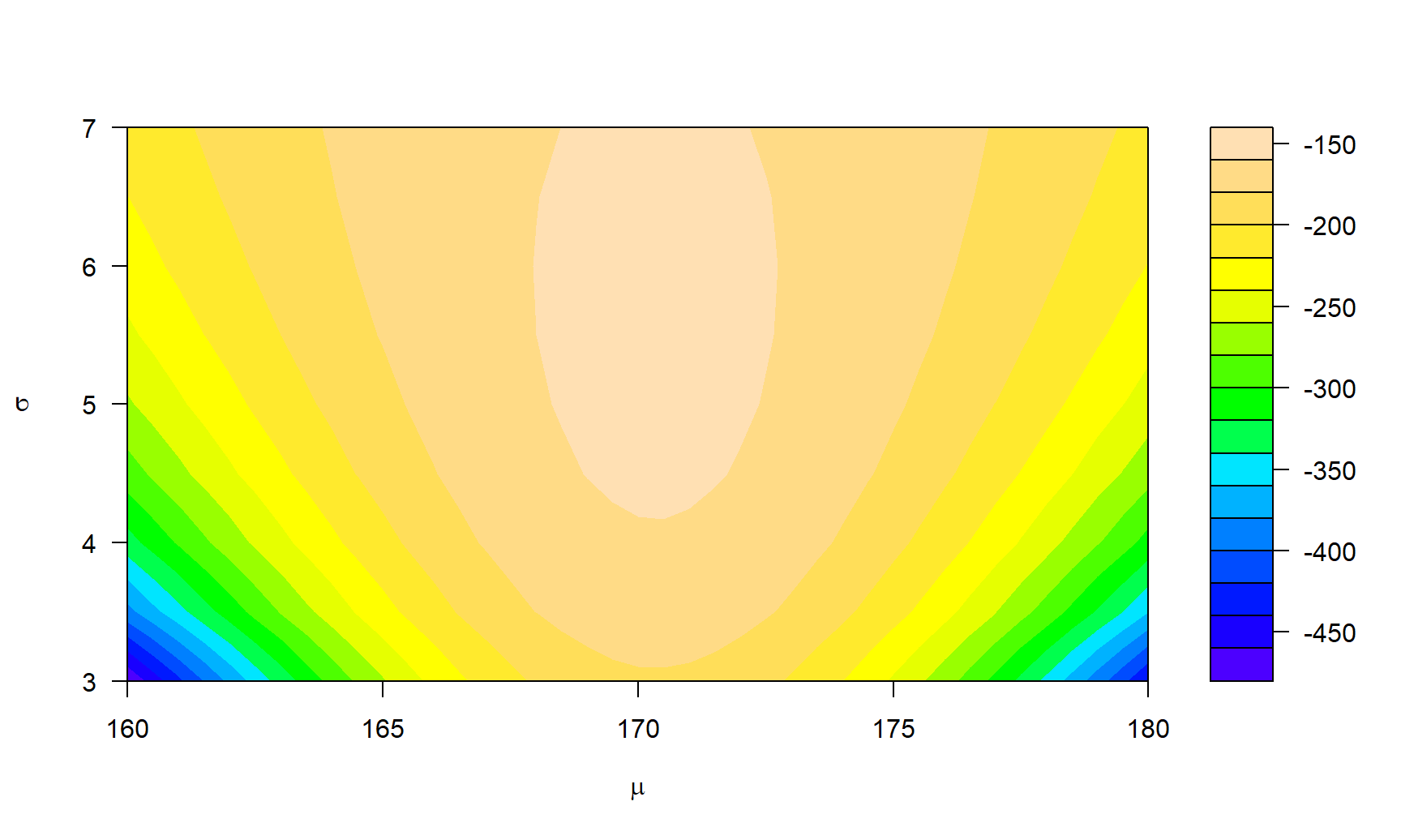

Figure 21.3: Gráfico de niveles para la función de log-verosimilitud para el ejemplo sobre normal.

3. Obtenga los valores de \(\mu\) y \(\sigma\) que maximizan la función de log-verosimilitud.

Para obtener los valores solicitados vamos a usar la función nlminb que es un optimizador. A la función nlminb se le debe indicar por medio del parámetro objective la función que queremos optimizar (minimizar); el parámetro start es un vector con los valores iniciales para comenzar la búsqueda de \(\mu\) y \(\sigma\); los parámetros lower y upper sirven para delimitar el espacio de búsqueda. A continuación se muestra el código usado para obtener los valores que minimizan a minusll, es decir, los valores que maximizan la función de log-verosimilitud.

minusll <- function(x) -ll(x)
nlminb(objective=minusll, start=c(163, 3.4),
       lower=c(160, 3), upper=c(180, 7))

## $par
## [1] 170.338374   5.423529
## 
## $objective
## [1] 155.4842
## 
## $convergence
## [1] 0
## 
## $iterations
## [1] 13
## 
## $evaluations
## function gradient 
##       16       35 
## 
## $message
## [1] "relative convergence (4)"

De la salida anterior podemos observar que los valores óptimos de \(\mu\) y \(\sigma\) son 170.338 y 5.424 respectivamente, resultado que coincide con lo observado en la Figura 21.3 y con los valores reales de simulación de la muestra. Esto indica que el procedimiento de estimación de parámetros por máxima verosimilitud entrega valores insesgados de los parámetros a estimar.

Un resultado interesante de la salida anterior es que se reporta el valor mínimo que alcanza la función minusll, este valor fue de 155.5, por lo tanto, se puede afirmar que el valor máximo de log-verosimilitud es -155.5.

Otros resultados importantes de la salida anterior son el valor de convergence=0 que indica que la búsqueda fue exitosa; iterations=13 indica que se realizaron 13 pasos desde el punto inicial start hasta las coordenadas de optimización.

En R se tienen dos funciones básicas para optimizar funciones, es decir, para encontrar los valores que minimizan una función dada. Esas dos funciones son nliminb y optim. Para optimizar en una sola dimensión se usa la función optimize.

4. ¿Hay alguna función para obtener directamente el valor que maximiza la función log-verosimilitud?

La respuesta es si. Si la distribución estudiada es una de las distribuciones básicas se puede usar la función fitdistr del paquete básico MASS. Esta función requiere de los datos que se ingresan por medio del parámetro x, y de la distribución de los datos que se ingresa por medio del parámetro densfun. La función fitdistr admite 15 distribuciones diferentes para hacer la búsqueda de los parámetros que caracterizan una distribución, se sugiere consultar la ayuda de la función fitdistr escribiendo en la consola help(fitdistr). A continuación el código usado.

require(MASS) # El paquete ya está instalado, solo se debe cargar
res <- fitdistr(x=y, densfun='normal')
res

##       mean           sd     
##   170.3383794     5.4235271 
##  (  0.7670026) (  0.5423527)

El objeto res contiene los resultados de usar fitdistr. En la primer línea están los valores de los parámetros que maximizan la función de log-verosimilitud, en la parte de abajo, dentro de paréntesis, están los errores estándar o desviaciones de éstos estimadores.

Al objeto res es de la clase fitdistr y por lo tanto se le puede aplicar la función genérica logLik para obtener el valor de la log-verosimilitud. Se sugiere consultar la ayuda de la función logLik escribiendo en la consola help(logLik). A continuación el código para usar logLik sobre el objeto res.

logLik(res)

## 'log Lik.' -155.4842 (df=2)

De esta última salida se observa que el valor coincide con el obtenido cuando se usó nlminb.

Ejemplo

Generar \(n=100\) observaciones de una gamma con parámetro de forma igual a 2, parámetro de tasa igual a 0.5 y luego responder las preguntas.

1. ¿Cómo se puede generar la muestra aleatoria solicitada?

Para generar la muestra aleatoria (ma) solicitada se fijó la semilla con el objetivo de que el lector pueda obtener los mismos resultados de este ejemplo.

n <- 100
set.seed(12345)
ma <- rgamma(n=n, shape=2, rate=0.5)

2. Asumiendo que la muestra aleatoria proviene de una normal (lo cual es incorrecto), estime los parámetros de la distribución normal.

fit1 <- fitdistr(x=ma, densfun='normal')
fit1

##      mean         sd    
##   4.3082767   2.8084910 
##  (0.2808491) (0.1985903)

3. Asumiendo que la muestra aleatoria proviene de una gamma estime los parámetros de la distribución gamma.

fit2 <- fitdistr(x=ma, densfun='gamma')
fit2

##      shape         rate   
##   2.23978235   0.51987909 
##  (0.29620136) (0.07702892)

En la salida anterior están los valores estimados de los parámetros de la distribución por el método de máxima verosimilitud, observe la cercanía de éstos con los verdaderos valores de 2 y 0.5 para forma y tasa respectivamente.

4. Dibuje dos qqplot, uno asumiendo distribución normal y el otro distribución gamma. ¿Cuál distribución se ajusta mejor a los datos simulados?

Para dibujar el qqplot se usa la función genérica qqplot, recomendamos consultar Hernández (2018) para los detalles de cómo usar esta función. Al usar qqplot para obtener el qqplot normal y gamma es necesario indicar los valores \(\hat{\boldsymbol{\theta}}\) obtenidos en el numeral anterior, por eso es que en el código mostrado a continuación aparece mean=4.3083, sd=2.8085 en el qqplot normal y shape=2.23978, rate=0.51988 en el qqplot gamma.

par(mfrow=c(1, 2))

qqplot(y=ma, pch=19,
       x=qnorm(ppoints(n), mean=4.3083, sd=2.8085),
       main='Normal Q-Q Plot',
       xlab='Theoretical Quantiles',
       ylab='Sample Quantiles')

qqplot(y=ma, pch=19,
       x=qgamma(ppoints(n), shape=2.23978, rate=0.51988),
       main='Gamma Q-Q Plot',
       xlab='Theoretical Quantiles',
       ylab='Sample Quantiles')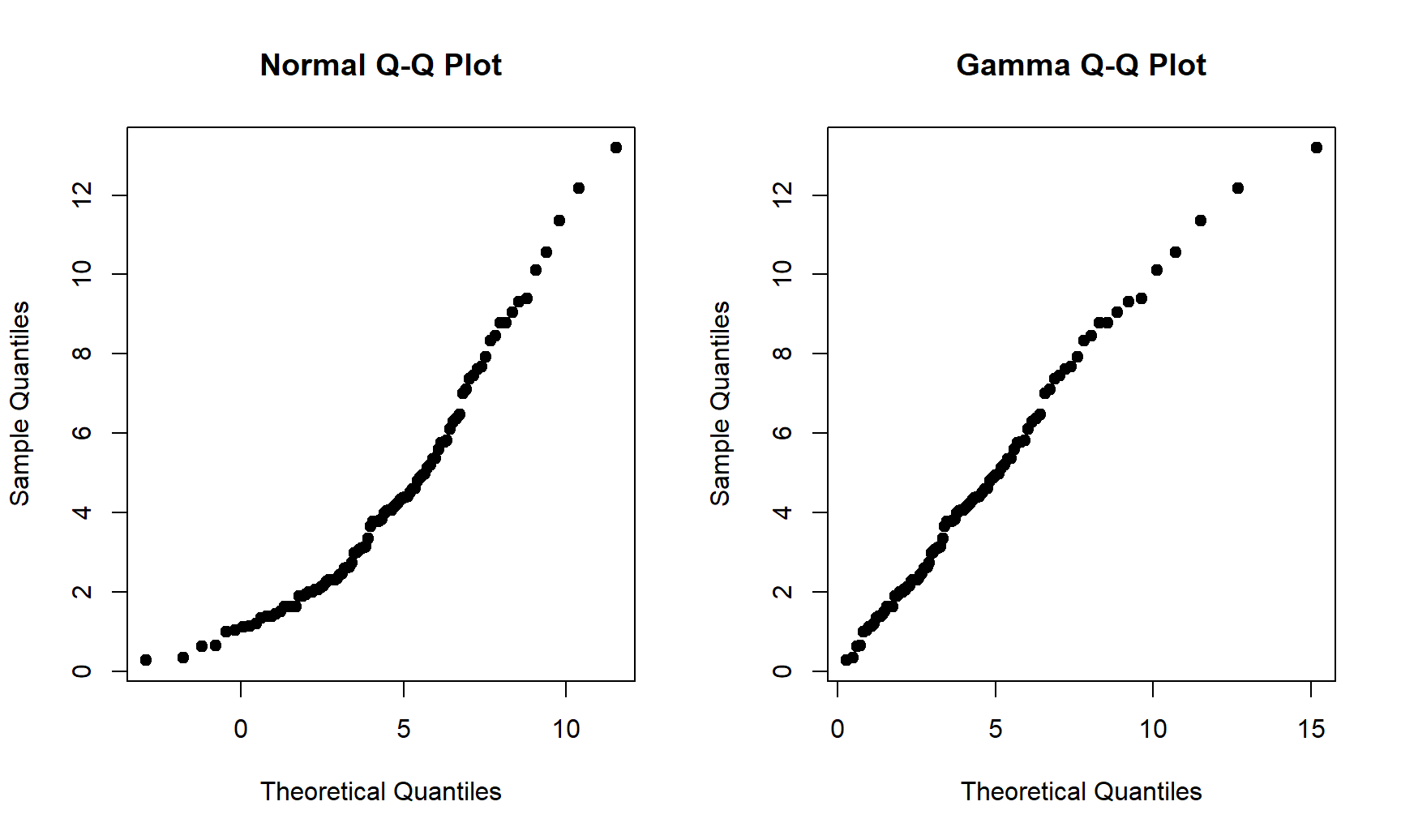

Figure 21.4: Gráfico cuantil cuantil normal y gamma para la muestra simulada.

En la Figura 21.4 se muestran los qqplot solicitados. Se observa claramente que al asumir normalidad (lo cual es incorrecto), los puntos del qqplot no están alineados, mientras que al asumir distribución gamma (lo cual es correcto), los puntos si están alineados. De esta figura se concluye que la muestra ma puede provenir de una \(Gamma(2.23978, 0.51988)\).

Para obtener el gráfico cuantil cuantil bajo normalidad se puede usar directamente la función qqnorm, consultar Hernández (2018) para mayores detalles.

En este ejemplo se eligió la mejor distribución entre dos candidatas usando una herramienta gráfica, lo que se recomienda usar algún método menos subjetivo (cuantitativo) para tomar decisiones.

5. Para comparar modelos se puede utilizar el Akaike information criterion (\(AIC\)) propuesto por Akaike (1974) que sirve para medir la calidad relativa de los modelos estadísticos, la expresión para calcular el indicador es \(AIC=-2 \, \hat{l}+2 \, df\), donde \(\hat{l}\) corresponde al valor de \(\log\)-verosimilitud y \(df\) corresponde al número de parámetros estimados del modelo. Siempre el modelo elegido es aquel modelo con el menor valor de \(AIC\). Calcular el \(AIC\) para los modelos asumidos normal y gamma.

-2 * logLik(fit1) + 2 * 2  # AIC para modelo normal

## 'log Lik.' 494.3172 (df=2)

-2 * logLik(fit2) + 2 * 2  # AIC para modelo gamma

## 'log Lik.' 466.0479 (df=2)

De los resultados anteriores se concluye que entre los dos modelos, el mejor es el gamma porque su \(AIC=466\) es el menor de toos los \(AIC\).

Modelos anidados pueden ser comparados por medio del global deviance (\(GD\)) dado por \(GD=-2 \, \hat{l}\) y modelos no anidados por medio del Generalized Akaike information criterion (\(GAIC\)) propuesto por Akaike (1983) y dado por \(GAIC=-2 \, \hat{l} + \sharp \, df\) siendo \(\sharp\) el valor de penalidad por cada parámetro adicional en el modelo; cuando \(\sharp = 2\), el \(GAIC\) coincide con el \(AIC\) y el Schwarz Bayesian criterion (\(SBC\)) propuesto por Schwarz (1978) se dá cuando el valor de penalidad es \(\sharp = \log(n)\) donde \(n\) es el número de observaciones del modelo; siempre el modelo elegido es aquel modelo con el menor valor de cualquiera de los criterios de información anteriores.

21.4 Score e Información de Fisher

En esta sección se explican los conceptos y utilidad de la función Score y la Información de Fisher.

21.4.1 Score e Información de Fisher en el caso univariado.

La función Score denotada por \(S(\theta)\) se define como la primera derivada de la función de log-verosimilitud así:

\[ S(\theta) \equiv \frac{\partial}{\partial \theta} l(\theta) \]

y el estimador de máxima verosimilitud \(\hat{\theta}\) se encuentra solucionando la igualdad

\[ S(\theta) = 0 \]

En el valor máximo \(\hat{\theta}\) la curva \(l(\theta)\) es cóncava hacia abajo y por lo tanto la segunda derivada es negativa, así la curvatura \(I(\theta)\) se define como

\[ I(\theta) \equiv - \frac{\partial^2}{\partial \theta^2} l(\theta) \]

Una curvatura grande \(I(\hat{\theta})\) está asociada con un gran pico en la función de log-verosimilitud y eso significa una menor incertidumbre sobre el parámetro \(\theta\) (Pawitan 2013). En particular la varianza del estimador de máxima verosimilitud está dada por

\[Var(\hat{\theta})=I^{-1}(\hat{\theta})\]

Ejemplo

Suponga que se desea estudiar una variable que tiene distribución Poisson con parámetro \(\lambda\) desconocido. Suponga además que se tienen dos situciones:

• Un solo valor 5 para estimar \(\lambda\).
• Cuatro valores 5, 10, 6 y 15 para estimar \(\lambda\).

Dibujar la función \(l(\lambda)\) para ambos casos e identificar la curvatura.

A continuación el código para evaluar la función \(l(\lambda)\) para cada caso.

# Caso 1
w <- c(5)
ll1 <- function(lambda) sum(dpois(x=w, lambda=lambda, log=T))
ll1 <- Vectorize(ll1)

# Caso 2
y <- c(5, 10, 6, 15)
ll2 <- function(lambda) sum(dpois(x=y, lambda=lambda, log=T))
ll2 <- Vectorize(ll2)

En la Figura 21.5 se muestran las dos curvas \(l(\lambda)\) para cada uno de los casos. De la figura se observa claramente que cuando se tienen 4 observaciones la curva es más puntiaguda y por lo tanto menor incertibumbre sobre el parámetro \(\lambda\) a estimar.

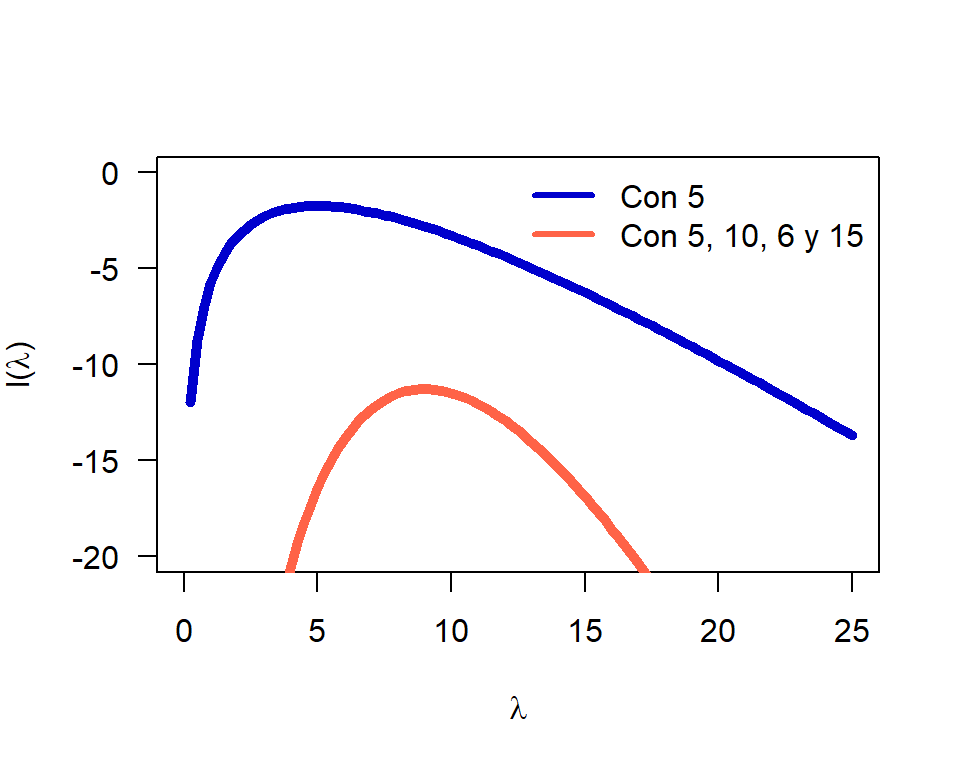
Figure 21.5: Curvas de log-verosimilitud para los dos casos.

21.5 Método de máxima verosimilitud para estimar parámetros en modelos de regresión

En esta sección se mostrará como estimar los parámetros de un modelo de regresión general.

Ejemplo

Considere el modelo de regresión mostrado abajo. Simule 1000 observaciones del modelo y use la función optim para estimar los parámetros del modelo.

\[\begin{align*} y_i &\sim N(\mu_i, \sigma^2), \\ \mu_i &= -2 + 3 x_1, \\ \sigma &= 5, \\ x_1 &\sim U(-5, 6). \end{align*}\]

El código mostrado a continuación permite simular un conjunto de valores con la estructura anteior.

n <- 1000
x1 <- runif(n=n, min=-5, max=6)
y <- rnorm(n=n, mean=-2 + 3 * x1, sd=5)

El vector de parámetros del modelo anterior es \(\boldsymbol{\theta}=(\beta_0, \beta_1, \sigma)^\top=(-2, 3, 5)^\top\), el primer elemento corresponde al intercepto, el segundo a la pendiente y el último a la desviación.

minusll <- function(theta, y, x1) {
  media <- theta[1] + theta[2] * x1  # Se define la media
  desvi <- theta[3]                  # Se define la desviación.
  - sum(dnorm(x=y, mean=media, sd=desvi, log=TRUE))
}

Ahora vamos a usar la función optim para encontrar los valores que maximizan la función de log-verosimilitud, el código para hacer eso se muestra a continuación. En el parámetro par se coloca un vector de posibles valores de \(\boldsymbol{\theta}\) para iniciar la búsqueda, en fn se coloca la función de interés, en lower y upper se colocan vectores que indican los límites de búsqueda de cada parámetro, los \(\beta_k\) pueden variar entre \(-\infty\) y \(\infty\) mientras que el parámetro \(\sigma\) toma valores en el intervalo \((0, \infty)\). Como la función minusll tiene argumentos adicionales y e x1, estos pasan a la función optim al final como se muestra en el código.

res1 <- optim(par=c(0, 0, 1), fn=minusll, method='L-BFGS-B',
              lower=c(-Inf, -Inf, 0), upper=c(Inf, Inf, Inf), 
              y=y, x1=x1)

En el objeto res1 está el resultado de la optimización, para explorar los resultados usamos

res1

## $par
## [1] -1.904603  3.079600  5.014184
## 
## $value
## [1] 3031.209
## 
## $counts
## function gradient 
##       19       19 
## 
## $convergence
## [1] 0
## 
## $message
## [1] "CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH"

De la salida anterior se observa que el vector de parámetros estimado es \(\hat{\beta}_0 = -1.9046025\), \(\hat{\beta}_1 = 3.0796\) y \(\hat{\sigma} = 5.0141842\), se observa también que el valor de la máxima log-verosimilitud fue de -3031.2092104. Vemos entonces que el vector estimado está muy cerca del verdadero \(\boldsymbol{\theta}=(\beta_0=-2, \beta_1=3, \sigma=5)^\top\).

Cuando se usa optim es necesario decirle que inicie la búsqueda de \(\boldsymbol{\theta}\) a partir de un lugar. Por esa razón se usó par=c(0, 0, 1), esto significa que la búsqueda inicia en el tripleta \(\beta_0=0\), \(\beta_1=0\) y \(\sigma=1\).

En algunas ocasiones es mejor hacer la búsqueda de los parámetros en el intervalo \((-\infty, \infty)\) que en una región limitada como por ejemplo \((0, \infty)\) o \((-1, 1)\), ya que las funciones de búsqueda podrían tener problemas en los bordes de esos intervalos. Una estrategia usual en este tipo de casos es aplicar una transformación apropiada al parámetro que tiene el dominio limitado. En el presente ejemplo \(\sigma\) sólo puede tomar valores mayores que cero y una transformación de tipo \(\log\) podría ser muy útil ya que \(\log\) relaciona los reales positivos con todos los reales. La transformación para este problema sería \(\log(\sigma)=\beta_3\) o escrita de forma inversa \(\sigma=\exp(\beta_3)\). El nuevo parámetro \(\beta_3\) puede variar en \((-\infty, \infty)\) pero al ser transformado por la función exponencial este se volvería un valor apropiado para \(\sigma\). Para implementar esta variación lo único que se debe hacer es modificar la línea 3 de la función minusll como se muestra a continuación:

minusll <- function(theta, y, x1) {
  media <- theta[1] + theta[2] * x1  
  desvi <- exp(theta[3])  # <<<<<---- El cambio fue aquí
  - sum(dnorm(x=y, mean=media, sd=desvi, log=TRUE))
}

Para hacer la búsqueda se procede de forma similar, abajo el código necesario.

res2 <- optim(par=c(0, 0, 0), fn=minusll, method='L-BFGS-B',
              y=y, x1=x1)
res2

## $par
## [1] -1.904609  3.079598  1.612271
## 
## $value
## [1] 3031.209
## 
## $counts
## function gradient 
##       21       21 
## 
## $convergence
## [1] 0
## 
## $message
## [1] "CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH"

De la salida anterior se observa que el vector de parámetros estimado es \(\hat{\beta}_0 = -1.9046094\), \(\hat{\beta}_1 = 3.0795984\) y \(\hat{\sigma} = \exp(1.6122706)=5.0141834\), se observa también que el valor de la máxima log-verosimilitud fue de -3031.2092104. Vemos entonces que el vector estimado está muy cerca del verdadero \(\boldsymbol{\theta}=(\beta_0=-2, \beta_1=3, \sigma=5)^\top\).

21.6 Paquete maxLik

El paquete maxLik tiene un conjunto de funciones útiles para estación por máxima verosimilitud y varias viñetas que pueden ser consultadas en este enlace.

Ejemplo

En este ejemplo vamos a repetir un ejemplo anterior con la distribución normal.

set.seed(1235)  # La semilla es 1235
y <- rnorm(n=50, mean=170, sd=5)
y[1:7]  # Para ver los primeros siete valores generados

## [1] 166.5101 163.5757 174.9498 170.5589 170.5710 178.4910 170.2392

Ahora vamos a crear la función de log-verosimilitud de la siguiente manera:

ll <- function(param) {
  media <- param[1]  # param es el vector de parámetros
  desvi <- param[2] 
  sum(dnorm(x=y, mean=media, sd=desvi, log=TRUE))
}

Ahora vamos a estimar los parametros con el paquete maxLik.

library(maxLik)

A <- matrix(c(1, 0,
              0, 1), byrow=TRUE, ncol=2)
B <- c(0, 0)

m <- maxLik(ll, start=c(media=163, desvi=3.4),
            constraints=list(ineqA=A, ineqB=B))
summary(m)

## --------------------------------------------
## Maximum Likelihood estimation
## Nelder-Mead maximization, 65 iterations
## Return code 0: successful convergence 
## Log-Likelihood: -155.4842 
## 2  free parameters
## Estimates:
##       Estimate Std. error t value Pr(> t)    
## media 170.3384     0.7789  218.70  <2e-16 ***
## desvi   5.4246     0.5415   10.02  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Warning: constrained likelihood estimation. Inference is probably wrong
## Constrained optimization based on constrOptim 
## 1  outer iterations, barrier value 0.06674455 
## --------------------------------------------

EJERCICIOS

1. Al inicio del Capítulo 11 se presentó la base de datos sobre medidas del cuerpo, consulte la explicación sobre la base de datos y responda lo siguiente.

• Si se asume que la edad tiene distribución normal, ¿cuáles son los estimadores de máxima verosimilitud para \(\mu\) y \(\sigma\)?
• Como el histograma para la edad muestra un sesgo a la derecha se podría pensar que la distribución gamma sería una buena candidata para explicar las edades observadas. Asumiendo una distribución gamma, ¿cuáles son los estimadores de máxima verosimilitud para los parámetros?
• ¿Cuál de los dos modelos es más apropiado para explicar la variable de interés? Calcule el \(AIC\) para decidir.

2. En el capítulo 17 se presentó un ejemplo donde se usó la base de datos sobre cangrejos hembra. Consulte la explicación sobre la base de datos y responda lo siguiente.

• Suponga que el número de satélites sobre cada hembra es una variable que se distribuye Poisson. Construya en R la función de log-verosimilitud \(l\), dibuje la función \(l\) y encuentre el estimador de máxima verosimilitud de \(\lambda\).
• Repita el ejercicio anterior asumiendo que el número de satélites se distribuye binomial negativo.
• ¿Cuál de los dos modelos es más apropiado para explicar la variable de interés? Calcule el \(AIC\) para decidir.

3. Al inicio del Capítulo 12 se presentó la base de datos sobre apartamentos usados en Medellín, consulte la explicación sobre la base de datos y responda lo siguiente.

• Dibuje una densidad para la variable área del apartamento.
• Describa lo encontrado en esa densidad.
• ¿Qué distribuciones de 2 parámetros podrían explicar el comportamiento del área de los apartamentos? Mencione al menos 3.
• Para cada una de las distribuciones anteriores dibuje un gráfico de contornos o calor para la función de log-verosimilitud y estime los parámetros de la distribución elegida.
• ¿Cuál de los dos modelos es más apropiado para explicar la variable de interés? Calcule el \(AIC\) para decidir.

4. Considere el siguiente modelo de regresión.

\[\begin{align*} y_i &\sim Gamma(shape_i, scale_i), \\ \log(shape_i) &= 3 - 7 x_1, \\ \log(scale_i) &= 3 - 1 x_2, \\ x_1 &\sim U(0, 1), \\ x_2 &\sim Poisson(\lambda=3) \end{align*}\]

• Simule 100 observaciones del modelo anterior.
• Escriba el vector de parámetros del problema.
• Construya la función minusll para el problema.
• Use la función optim para estimar los parámetros del problema.

References

Akaike, H. 1974. “A new look at the statistical model identification.” IEEE Transactions on Automatic Control 19 (6): 716–23.

———. 1983. “Information measures and model selection.” Bulletin of the International Statistical Institute 50: 277–90.

Fisher, R. A. 1922. “On the Mathematical Foundations of Theoretical Statistics.” Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character 222: 309–68. http://www.jstor.org/stable/91208.

Hernández, J., F. & Correa. 2018. Gráficos Con R. Primera. Medellín, Colombia: Universidad Nacional de Colombia. https://fhernanb.github.io/Graficos-con-R/.

Pawitan, Yudi. 2013. In All Likelihood: Statistical Modelling and Inference Using Likelihood. Oxford University Press.

Schwarz, G. 1978. “Estimating the dimension of a model.” Annals of Statistics 6 (2): 461–64.