17 Distribuciones discretas
En este capítulo se mostrarán las funciones de R para distribuciones discretas.
17.1 Funciones disponibles para distribuciones discretas
Para cada distribución discreta se tienen 4 funciones, a continuación el listado de funciones y su utilidad.
dxxx(x, ...) # Función de masa de probabilidad, f(x)
pxxx(q, ...) # Función de distribución acumulada hasta q, F(x)
qxxx(p, ...) # Cuantil para el cual P(X <= q) = p
rxxx(n, ...) # Generador de números aleatorios.En el lugar de las letras xxx se de debe colocar el nombre de la distribución en R, a continuación el listado de nombres disponibles para las 6 distribuciones discretas básicas.
binom # Binomial
geo # Geométrica
nbinom # Binomial negativa
hyper # Hipergeométrica
pois # Poisson
multinom # MultinomialCombinando las funciones y los nombres se tiene un total de 24 funciones, por ejemplo, para obtener la función de masa de probabilidad \(f(x)\) de una binomial se usa la función dbinom( ) y para obtener la función acumulada \(F(x)\) de una Poisson se usa la función ppois( ).
Ejemplo binomial
Suponga que un grupo de agentes de tránsito sale a una vía principal para revisar el estado de los buses de transporte intermunicipal. De datos históricos se sabe que un 10% de los buses generan una mayor cantidad de humo de la permitida. En cada jornada los agentes revisan siempre 18 buses, asuma que el estado de un bus es independiente del estado de los otros buses.
- Calcular la probabilidad de que se encuentren exactamente 2 buses que generan una mayor cantidad de humo de la permitida.
Aquí se tiene una distribucion \(Binomial(n=18, p=0.1)\) y se desea calcular \(P(X=2)\). Para obtener esta probabilidad se usa la siguiente instrucción.
## [1] 0.2835121Así \(P(X=2)=0.2835\).
- Calcular la probabilidad de que el número de buses que sobrepasan el límite de generación de gases sea al menos 4.
En este caso interesa calcular \(P(X \geq 4)\), para obtener esta probabilidad se usa la siguiente instrucción.
## [1] 0.09819684Así \(P(X \geq 4)=0.0982\)
- Calcular la probabilidad de que tres o menos buses emitan gases por encima de lo permitido en la norma.
En este caso interesa \(P(X\leq3)\) lo cual es \(F(x=3)\), por lo tanto, la instrucción para obtener esta probabilidad es
## [1] 0.9018032Así \(P(X\leq3)=F(x=3)=0.9018\)
- Dibujar la función de masa de probabilidad.
Para dibujar la función de masa de probabilidad para una \(Binomial(n=18, p=0.1)\) se usa el siguiente código.
x <- 0:18 # Soporte (dominio) de la variable
Probabilidad <- dbinom(x=x, size=18, prob=0.1)
plot(x=x, y=Probabilidad,
type='h', las=1, lwd=6)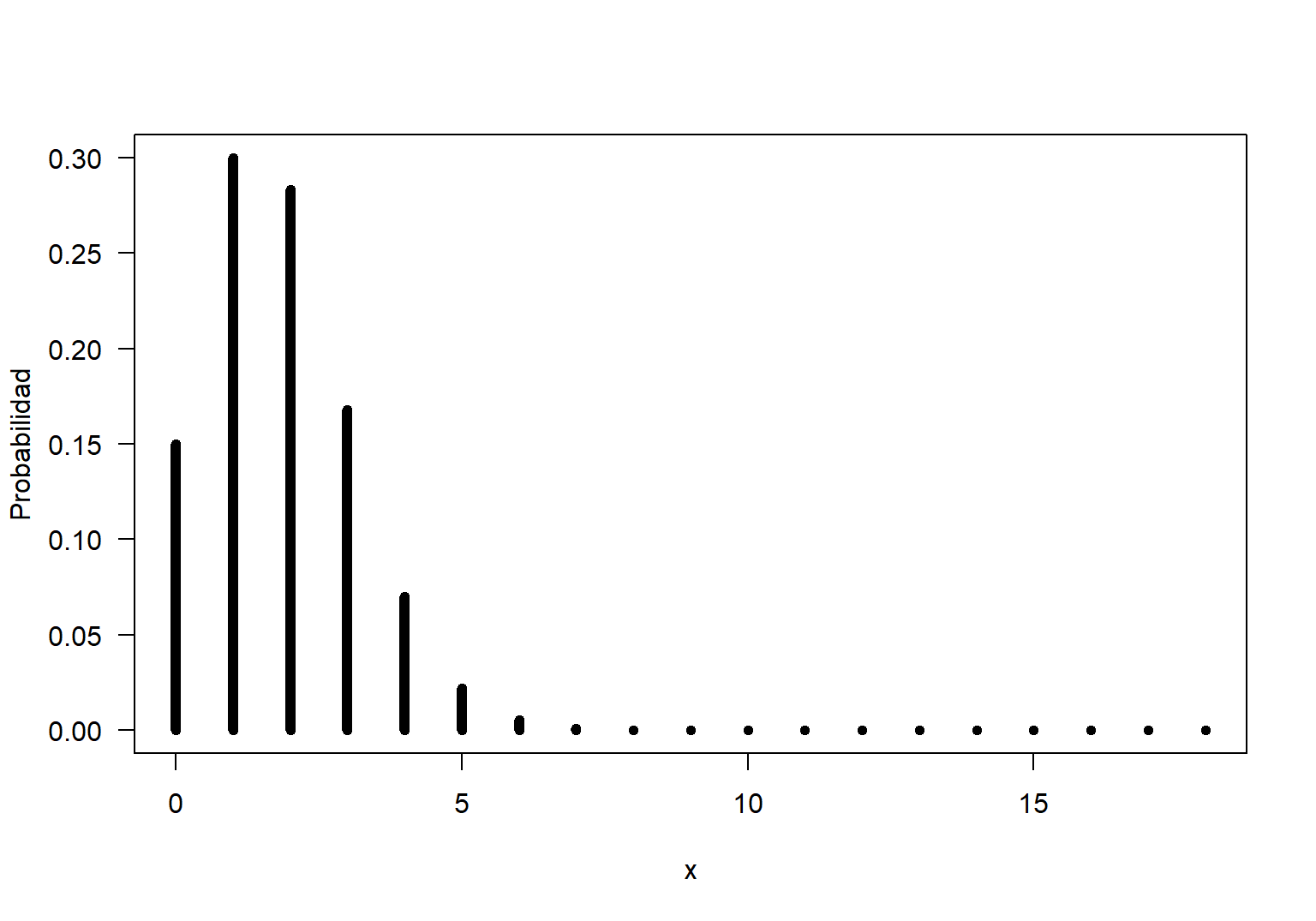
Figure 17.1: Función de masa de probabilidad para una \(Binomial(n=18, p=0.1)\).
En la Figura 17.1 se muestra la función de masa de probabilidad para la \(Binomial(n=18, p=0.1)\), de esta figura se observa claramente que la mayor parte de la probabilidad está concentrada para valores pequeños de \(X\) debido a que la probabilidad de éxito individual es \(p=0.10\). Valores de \(X \geq 7\) tienen una probabilidad muy pequeña y es por eso que las longitudes de sus barras son muy cortas.
- Generar con 100 de una distribución \(Binomial(n=18, p=0.1)\) y luego calcular las frecuencias muestrales y compararlas con las probabilidades teóricas.
La muestra aleatoria se obtiene con la función rbinom y los resultados se almacenan en el objeto m, por último se construye la tabla de frecuencias relativas, a continuación el código usado.
## [1] 2 1 2 4 2 1 3 2 1 4 3 0 3 1 3 2 3 2 3 3 3 4 1 4 2 2 2 4 0 1 2 4 2 0 5 3 1
## [38] 1 1 1 2 0 3 3 2 3 3 2 3 1 0 1 3 0 2 4 1 4 2 1 1 1 3 0 1 1 3 2 2 1 2 1 3 3
## [75] 2 2 3 3 1 3 1 0 5 2 2 0 3 2 1 1 1 3 1 1 1 2 3 3 1 1## m
## 0 1 2 3 4 5
## 0.09 0.30 0.25 0.26 0.08 0.02A pesar de ser una muestra aleatoria de sólo 100 observaciones, se observa que las frecuencias relativas obtenidas son muy cercanas a las mostradas en la Figura 17.1.
Ejemplo geométrica
En una línea de producción de bombillos se sabe que sólo el 1% de los bombillos son defectuosos. Una máquina automática toma un bombillo y lo prueba, si el bombillo enciende, se siguen probando los bombillos hasta que se encuentre un bombillo defectuoso, ahí se para la línea de producción y se toman los correctivos necesarios para mejorar el proceso.
- Calcular la probabilidad de que se necesiten probar 125 bombillos para encontrar el primer bombillo defectuoso.
En la distribución geométrica, la variable \(X\) representa el número de fracasos antes de encontrar el único éxito, por lo tanto, en este caso el interés es calcular \(P(X=124)\). La instrucción para obtener esta probabiliad es la siguiente.
## [1] 0.002875836- Calcular \(P(X \leq 8)\).
En este caso interesa \(P(X \leq 50)\) lo que equivale a \(F(8)\), la instrucción para obtener la probabilidad es la siguiente.
## [1] 0.401044- Encontrar el cuantil \(q\) tal que \(P(X \leq q) = 0.40\).
En este caso interesa encontrar el cuantil \(q\) que cumpla la condición de que hasta \(q\) esté el 40% de las observaciones, por esa razón se usa la función qgeom como se muestra a continuación.
## [1] 50pxxx y qxxx están relacionadas, pxxx entrega la probabilidad hasta el cuantil \(q\) mientras qxxx entrega el cuantil en el que se acumula \(p\) probabilidad.
Ejemplo binomial negativa
Una familia desea tener hijos hasta conseguir 2 niñas, la probabilidad individual de obtener una niña es 0.5 y se supone que todos los nacimientos son individuales, es decir, un sólo bebé.
- Calcular la probabilidad de que se necesiten 4 hijos, es decir, 4 nacimientos para consguir las dos niñas.
En este problema se tiene una distribución binomial negativa con \(r=2\) niñas, los éxitos deseados por la familia. La variable \(X\) representa los fracasos, es decir los niños, hasta que se obtienen los éxitos \(r=2\) deseados.
En este caso lo que interesa es \(P(\text{familia tenga 4})\), en otras palabras interesa \(P(X=2)\), la instrucción para calcular la probabilidad es la siguiente.
## [1] 0.1875- Calcular \(P(\text{familia tenga al menos 4 hijos})\).
Aquí interesa calcular \(P(X \geq 2)=P(X=2)+P(X=3)+\ldots\), como esta probabilidad va hasta infinito, se debe usar el complemento así:
\[P(X \geq 2) = 1 - [P(X=0)+P(X=1)]\]
y para obtener la probabilidad solicitada se puede usar la función dnbinom de la siguiente manera.
## [1] 0.5Otra forma para obtener la probabilidad solicitada es por medio de la función pnbinom de la siguiente manera.
## [1] 0.5Ejemplo hipergeométrica
Un lote de partes para ensamblar en una empresa está formado por 100 elementos del proveedor A y 200 elementos del proveedor B. Se selecciona una muestra de 4 partes al azar sin reemplazo de las 300 para una revisión de calidad.
- Calcular la probabilidad de que todas las 4 partes de la muestra sean del proveedor A.
Aquí se tiene una situación que se puede modelar por medio de una distribución hipergeométrica con \(m=100\) éxitos en la población, \(n=200\) fracasos en la población y \(k=4\) el tamaño de la muestra. El objetivo es calcular \(P(X=4)\), para obtener esta probabilidad se usa la siguiente instrucción.
## [1] 0.01185408- Calcular la probabilidad de que dos o más de las partes sean del proveedor A.
Aquí interesa \(P(X \geq 2)\), la instrucción para obtener esta probabilidad es.
## [1] 0.4074057Ejemplo Poisson
En una editorial se asume que todo libro de 250 páginas tiene en promedio 50 errores.
- Encuentre la probabilidad de que en una página cualquiera no se encuentren errores.
Este es un problema de distribución Poisson con tasa promedio de éxitos dada por:
\[\lambda=\frac{50 \quad errores}{libro}=\frac{0.2 \quad errores}{pagina}\] El objetivo es calcular \(P(X=0)\), para obtener esta probabilidad de usa la siguiente instrucción.
## [1] 0.8187308Así \(P(X=0)=0.8187\).
17.2 Distribuciones discretas generales
En la práctica nos podemos encontramos con variables aleatorias discretas que no se ajustan a una de las distribuciones mostradas anteriormente, en esos casos, es posible manejar ese tipo de variables por medio de unas funciones básicas de R como se muestra en el siguiente ejemplo.
Ejemplo
El cangrejo de herradura hembra se caracteriza porque su caparazón se adhieren los machos de la misma especie, en la Figura 17.2 se muestra una fotografía de este cangrejo. Los investigadores están interesado en determinar cual es el patrón de variación del número de machos sobre cada hembra, para esto, se recolectó una muestra de hembras a las cuales se les observó el color, la condición de la espina, el peso en kilogramos, el ancho del caparazón en centímetros y el número de satélites o machos sobre el caparazón, la base de datos está disponible en el siguiente enlace.

Figure 17.2: Fotografía del cangrejo de herradura, tomada de http://sccoastalresources.com/home/2016/6/21/a-night-of-horseshoe-crab-tagging
- Encontrar la distribución de probabilidad para la variable
Saque corresponde al número de machos sobre el caparazón de cada hembra.
Primero se debe leer la base de datos usando la url suministrada y luego se construye la tabla de frecuencia relativa y se almacena en el objeto t1.
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/crab'
crab <- read.table(file=url, header=T)
t1 <- prop.table(table(crab$Sa))
t1##
## 0 1 2 3 4 5
## 0.358381503 0.092485549 0.052023121 0.109826590 0.109826590 0.086705202
## 6 7 8 9 10 11
## 0.075144509 0.023121387 0.034682081 0.017341040 0.017341040 0.005780347
## 12 14 15
## 0.005780347 0.005780347 0.005780347La anterior tabla de frecuencias relativas se puede representar gráficamente usando el siguiente código.
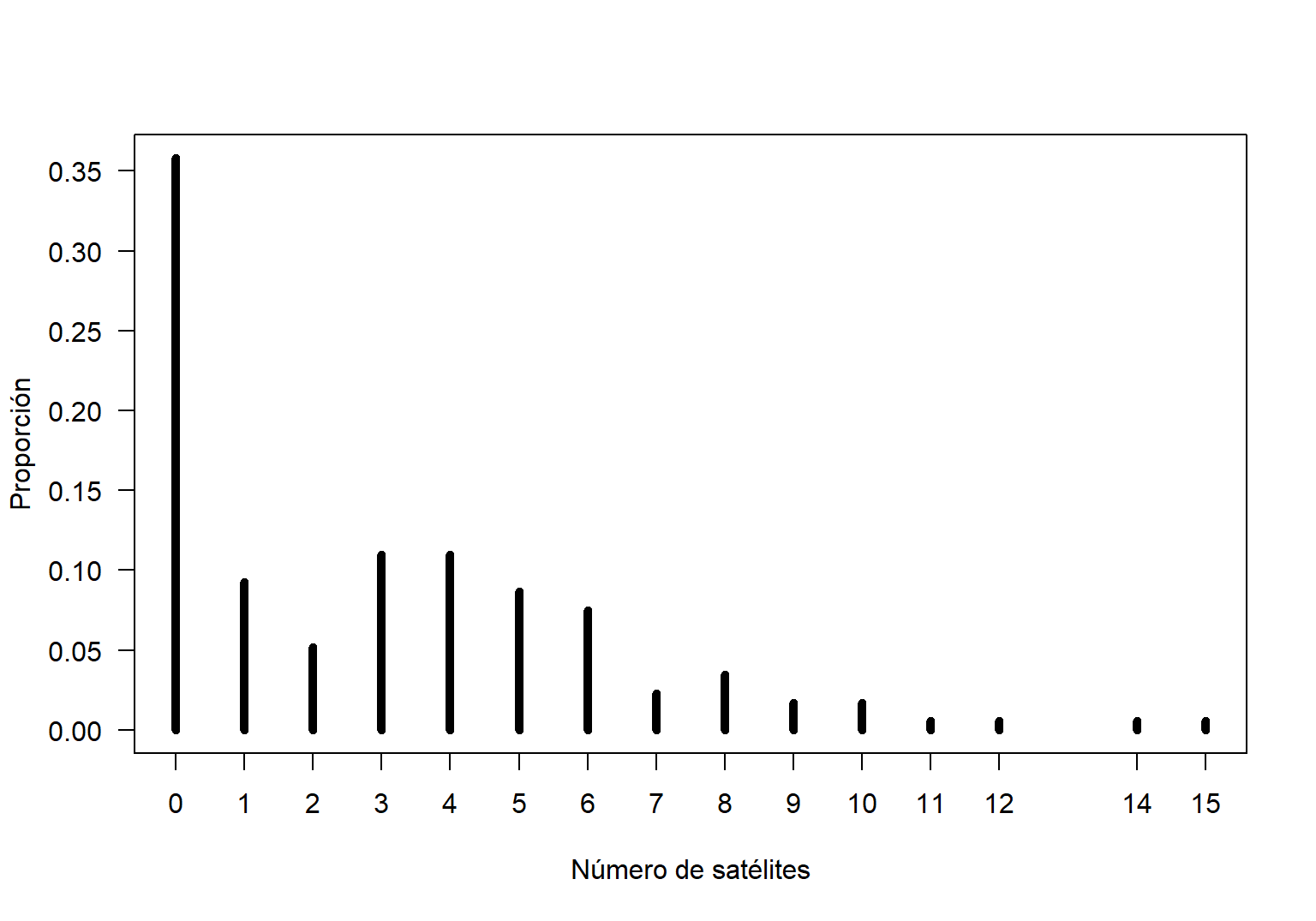
Figure 17.3: Función de masa de probabilidad para el número de satélites por hembra.
- Sea \(X\) la variable número de satélites por hembra, construir la función \(F(x)\).
Para construir \(F(x)\) se utiliza la función ecdf o empirical cumulative density function, a esta función le debe ingresar el vector con la información de la variable cuantitativa, a continuación del código usado. En la Figura 17.4 se muestra la función de distribución acumulada para para el número de satélites por hembra.
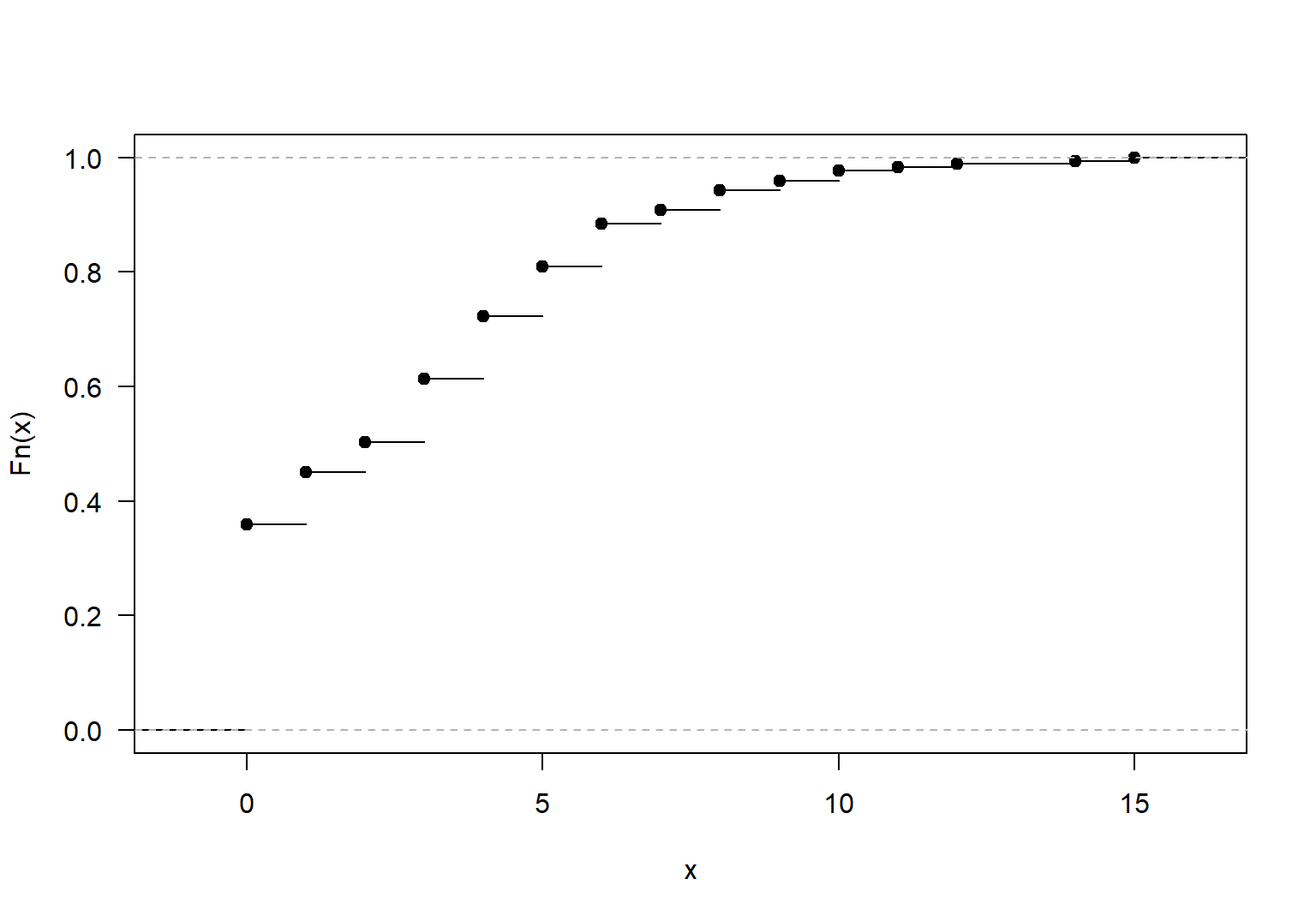
Figure 17.4: Función de distribución acumulada para el número de satélites por hembra.
- Calcular \(P(X \leq 9)\).
Para obtener esta probabilidad se usa el objeto F que es en realidad una función, a continuación la instrucción usada.
## [1] 0.9595376Así \(P(X \leq 9)=0.9595\).
- Calcular \(P(X > 4)\).
Para obtener esta probabilidad se usa el hecho de que \(P(X > 4) = 1 - P(X \leq 4)\), así la instrucción a usar es.
## [1] 0.2774566Por lo tanto \(P(X > 4)=0.2775\).
- Suponga que el grupo 1 está formado por las hembras cuyo ancho de caparazón es menor o igual al ancho mediano, el grupo 2 está formado por las demás hembras. ¿Será \(F(x)\) diferente para los dos grupos?
Para realizar esto vamos a particionar el vector Sa en los dos grupos de acuerdo a la nueva variable grupo creada como se muestra a continuacion.
El objeto x es una lista y para acceder a los vectores allí almacenados usamos dos corchetes [[]], uno dentro del otro. Luego para calcular \(F(x)\) para los dos grupos se procede así:
Para obtener las dos \(F(x)\) en la misma figura se usa el código siguiente.
plot(F1, col='blue', main='', las=1)
plot(F2, col='red', add=T)
legend('bottomright', legend=c('Grupo 1', 'Grupo 2'),
col=c('blue', 'red'), lwd=1)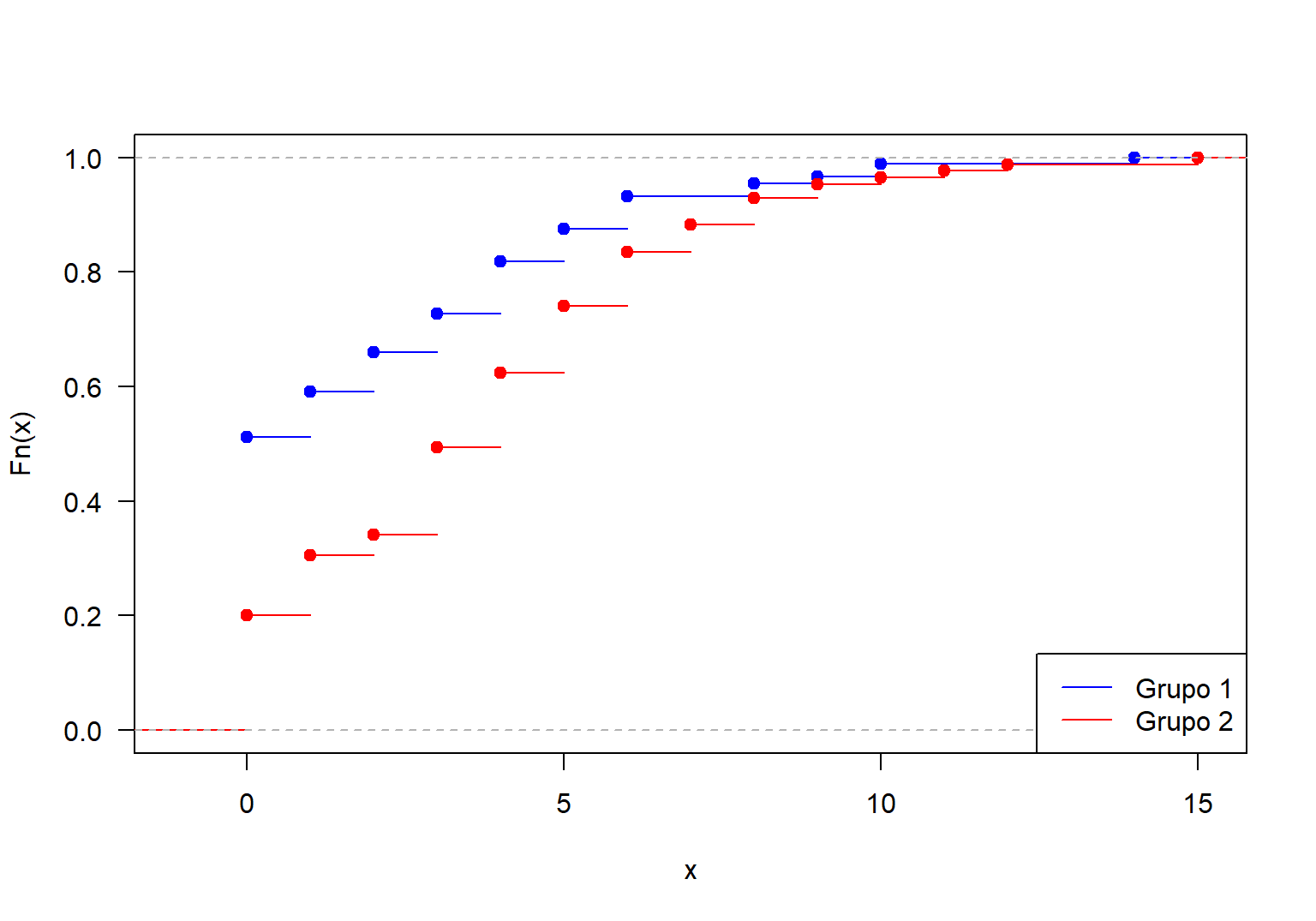
Figure 17.5: Función de distribución acumulada para el número de satélites por hembra diferenciando por grupo.
En la Figura 17.5 se muestran las dos \(F(x)\), en color azul para el grupo 1 y en color rojo para el grupo 2. Se observa claramente que las curvas son diferentes antes de \(x=9\). El hecho de que la curva azul esté por encima de la roja para valores menores de 9, es decir, \(F_1(x) \geq F_2(x)\), indica que las hembras del grupo 1 tienden a tener menos satélites que las del grupo 2, esto es coherente ya que las del grupo 2 son más grandes en su caparazón.