7 Creación de funciones en R

Uno de los atractivos de R es la gran cantidad de funciones que existen para realizar diversos procedimientos. En este capítulo se explica al lector la forma de crear sus propias funciones para que pueda realizar diversas tareas y así logre explotar el potencial que ofrece R.

7.1 ¿Qué es una función en R?

Una función es un conjunto de instrucciones que convierten las entradas (inputs) en resultados (outputs) deseados. En la siguiente figura se muestra una ilustración de lo que es una función.

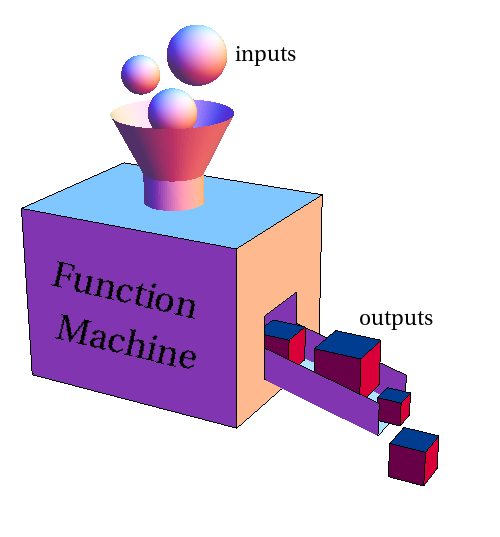
7.2 Partes de una función en R

Las partes de una función son:

Entradas o argumentos: sirven para ingresar información necesaria para realizar el procedimiento de la función. Los argumentos pueden estar vacíos y a la espera de que el usuario ingrese valores, o pueden tener valores por defecto, esto significa que si el usuario no ingresa un valor, la función usará el valor por defecto. Una función puede tener o no argumentos de entrada, en los ejemplos se mostrarán estos casos.
Cuerpo: está formado por un conjunto de instrucciones que transforman las entradas en las salidas deseadas. Si el cuerpo de la función está formado por varias instrucciones éstas deben ir entre llaves { }.
Salidas: son los resultados de la función. Toda función debe tener al menos un resultado. Si una función entrega varios tipos de objetos se acostumbra a organizarlos en una lista que puede manejar los diferentes tipos de objetos.

A continuación se muestra la estructura general de una función en R.

nombre_de_funcion <- function(par1, par2, ...) {
  cuerpo
  cuerpo
  cuerpo
  cuerpo
  return(resultado)
}

Se recomienda siempre que la última línea de la función tenga la instrucción return() para que quede en evidencia el resultado que la función retorna.

A continuación se mostrarán varios ejemplos sencillos para que el lector aprenda a construir funciones en R.

Ejemplo

Construir una función que reciba dos números y que entregue la suma de estos números.

Solución

Lo primero es elegir un nombre apropiado para la función, aquí se usó el nombre suma porque así se tiene una idea clara de lo que hace la función. La función suma recibe dos parámetros, x representa el primer valor ingresado mientras que y representa el segundo. El cuerpo de la función está formado por dos líneas, en la primera se crea el objeto resultado en el cual se almanacena el valor de la suma, en la segunda línea se le indica a R que queremos que retorne el valor de la suma almacenada en el objeto resultado. A continuación se muestra el código para crear la función solicitada.

suma <- function(x, y) {
  resultado <- x + y
  return(resultado)
}

Para usar la función creada sólo se debe ejecutar, vamos a obtener la suma de los valores 4 y 6 usando la función suma, a continuación el código necesario.

suma(x=4, y=6)

## [1] 10

Para funciones simples como la anterior es posible escribirlas en forma más compacta. Es posible reducir el cuerpo de la función de 2 líneas a sólo una línea solicitándole a R que retorne directamente la suma sin almacenarla en ningún objeto. A continuación la función suma modificada.

suma <- function(x, y) {
  return(x + y)
}

suma(x=4, y=6)  # Probando la función

## [1] 10

Debido a que la función suma tiene un cuerpo muy reducido es posible escribirla en forma más compacta, en una sola línea. A continuación se muestra el código para reescribir la función.

suma <- function(x, y) x + y

suma(x=4, y=6)  # Probando la función

## [1] 10

Ejemplo

Construir una función que genere números aleatorios entre cero y uno hasta que la suma de éstos números supere por primera vez el valor de 3. La función debe entregar la cantidad de números aleatorios generados para que se cumpla la condición.

Solución

Vamos a llamar la función solicitada con el nombre fun1, esta función NO necesita ningún parámetro de entrada. El valor de 3 que está en la condición puede ir dentro del cuerpo y por eso no se necesitan parámetros para esta función. En el cuerpo de la función se genera un vector con un número aleatorio y luego se chequea si la suma de sus elementos es menor de 3, si se cumple que la suma es menor que 3 se siguen generando números que se almacenan en el vector num. Una vez que la suma exceda el valor de 3 NO se ingresa al while y se pide la longitud del vector o el valor de veces solicitado. A continuación el código de la función.

fun1 <- function() {
  num <- runif(1)
  veces <- 1
  while (sum(num) < 3) {
    veces <- veces + 1
    num[veces] <- runif(1)
  }
  return(veces)
}

fun1()  # primera prueba

## [1] 8

Ejemplo

Construir una función que, dado un número entero positivo (cota) ingresado por el usuario, genere números aleatorios entre cero y uno hasta que la suma de los números generados exceda por primera vez la cota. La función debe entregar un vector con los números aleatorios, la suma y la cantidad de números aleatorios. Si el usuario no ingresa el valor de la cota, se debe asumir igual a 1.

Solución

La función aquí solicitada es similar a la construída en el ejemplo anterior. La función fun2 tiene un sólo parámetro con el valor por defecto, si el usuario no ingresa valor a este parámetro, se asumirá el valor de uno. El cuerpo de la función es similar al anterior. Como la función debe entregar un vector y dos números, se construye la lista resultado que almacena los tres objetos solicitados. A continuación el código para función solicitada.

fun2 <- function(cota=1) {
  num <- runif(1)
  while (sum(num) < cota) {
    num <- c(num, runif(1))
  }
  resultado <- list(vector=num,
                    suma=sum(num),
                    cantidad=length(num))
  return(resultado)
}

Probando la función con cota de uno.

fun2()

## $vector
## [1] 0.8523376 0.4814579
## 
## $suma
## [1] 1.333796
## 
## $cantidad
## [1] 2

Probando la función con cota de tres.

fun2(cota=3)

## $vector
## [1] 0.7703864 0.6567623 0.5173527 0.7785944 0.6926085
## 
## $suma
## [1] 3.415704
## 
## $cantidad
## [1] 5

Ejemplo

Construya una función que reciba dos números de la recta real y que entregue el punto médio de estos números. El resultado debe ser un mensaje por pantalla.

Solución

El punto médio entre dos valores es la suma de los números divido entre dos. La función cat sirve para concatenar objetos y presentarlos por pantalla. A continuación el código para la función requerida.

medio <- function(a, b) {
  medio <- (a + b) / 2
  cat("El punto medio de los valores", a, "y", b,
      "ingresados es", medio)
}

medio(a=-3, b=-1)  # Probando la función

## El punto medio de los valores -3 y -1 ingresados es -2

La función cat es muy útil para presentar resultados por pantalla. Consulte la ayuda de la función para ver otros ejemplos.

EJERCICIOS

Construir funciones en R que realicen lo solicitado.

Construya una función que reciba dos números reales a y b, la función debe decir cuál es el mayor de ellos.
Escriba una función llamada media que calcule la media muestral de un vector numérico x ingresado a la función. A continuación la fórmula para calcular la media muestral.

\[\bar{x}=\frac{\sum_{i=1}^n x_i}{n}\]

Nota: no puede usar la función mean( ).

Construya una función que encuentre las raíces de una ecuación de segundo grado. El usuario debe suministrar los coeficientes a, b y c de la ecuación \(ax^2+bx+c=0\) y la función debe entregar las raíces.
Escribir una función que calcule la velocidad de un proyectil dado que el usuario ingresa la distancia recorrida en Km y el tiempo necesario en minutos. Expresar el resultado se debe entregar en metros/segundo, recuerde que

\[velocidad = \frac{espacio}{tiempo}\] 5. Escribir una función que reciba dos valores \(a\) y \(b\) y que los intercambie. Es decir, si ingresa \(a=4\) y \(b=9\) que la función entregue \(a=9\) y \(b=4\).

Construya una función a la cual le ingrese el salario por hora y el número de horas trabajadas durante una semana por un trabajador. La función debe calcular el salario neto.
Construya una función llamada precio que calcule el precio total de sacar A fotocopias y B impresiones, sabiendo que los precios son 50 y 100 pesos para A y B respectivamente si el cliente es un estudiante, y de 75 y 150 para A y B si el cliente es un profesor. La función debe tener dos argumentos cuantitativos (A y B) y el argumento lógico estudiante que por defecto tenga el valor de TRUE. Use la estructura mostrada abajo.

precio <- function(A, B, estudiante=TRUE) {
  ...
  ...
  ...
  return(precio_total)
}

Construya una función llamada salario que le ingrese el salario por hora y el número de horas trabajadas durante una semana por un trabajador. La función debe calcular el salario neto semanal, teniendo en cuenta que si el número de horas trabajadas durante la semana es mayor de 48, esas horas de demás se consideran horas extras y tienen un 35% de recargo. Imprima el salario neto. Use la estructura mostrada abajo.

salario <- function(num.horas, valor_hora) {
  ...
  ...
  ...
  return(salario_neto)
}

Construya una función llamada nota que calcule la nota obtenida por un alumno en una evaluación de tres puntos cuya ponderación o importancia son 20%, 30% y 50% para los puntos I, II y III respectivamente. Adicionalmente la función debe generar un mensaje sobre si el estudiante aprobó la evaluación o no. El usuario debe ingresar las notas individuales de los tres puntos y la función debe entregar la nota final de la evaluación. Use la estructura mostrada abajo.

nota <- function(p1, p2, p3) {
  ...
  ...
  ...
}

Escriba una función llamada minimo que permita obtener el valor mínimo de un vector numérico. No puede usar ninguna de las funciones básicas de R como which.min(), which.max(), order(), min( ), max( ), sort( ) u order( ). Use la estructura mostrada abajo.

minimo <- function(x) {
  ...
  ...
  return(minimo)
}

Construya una función que calcule las coordenadas del punto medio \(M\) entre dos puntos \(A\) y \(B\). Vea la siguiente figura para una ilustración. ¿Cuáles cree usted que deben ser los parámetros de entrada de la función?