4 Predicción

En este capítulo se presenta una descripción breve de como realizar predicciones a partir de un modelo de regresión lineal.

Función `predict`

La función predict es una función genérica de clase S3 que se puede aplicar a un modelo ajustado para obtener los valores de \(\hat{y}\). Abajo se muestra la estructura de la función predict con la lista de sus argumentos.

predict.lm(object, newdata, se.fit = FALSE, scale = NULL, df = Inf, 
    interval = c("none", "confidence", "prediction"), 
    level = 0.95, type = c("response", "terms"), 
    terms = NULL, na.action = na.pass, pred.var = res.var/weights, 
    weights = 1, ...)

Ejemplo

Suponga que queremos ajustar un modelo de regresión para explicar el número de trabajadores empleados (Employed) en función de las covariables Unemployed, Armed.Forces y Year del conjunto de datos longley. Luego de ajustar el modelo queremos predecir el valor de \(E(Employed|\boldsymbol{X}=\boldsymbol{x}_0)\) en dos situaciones:

Año 1963 con 420 desempleados y 270 personas en fuerzas armadas.
Año 1964 con 430 desempleados y 250 personas en fuerzas armadas.

Solución

Primero exploremos los datos.

library(dplyr)
longley |> 
  select(Employed, Unemployed, Armed.Forces, Year) -> datos

plot(datos, pch=20)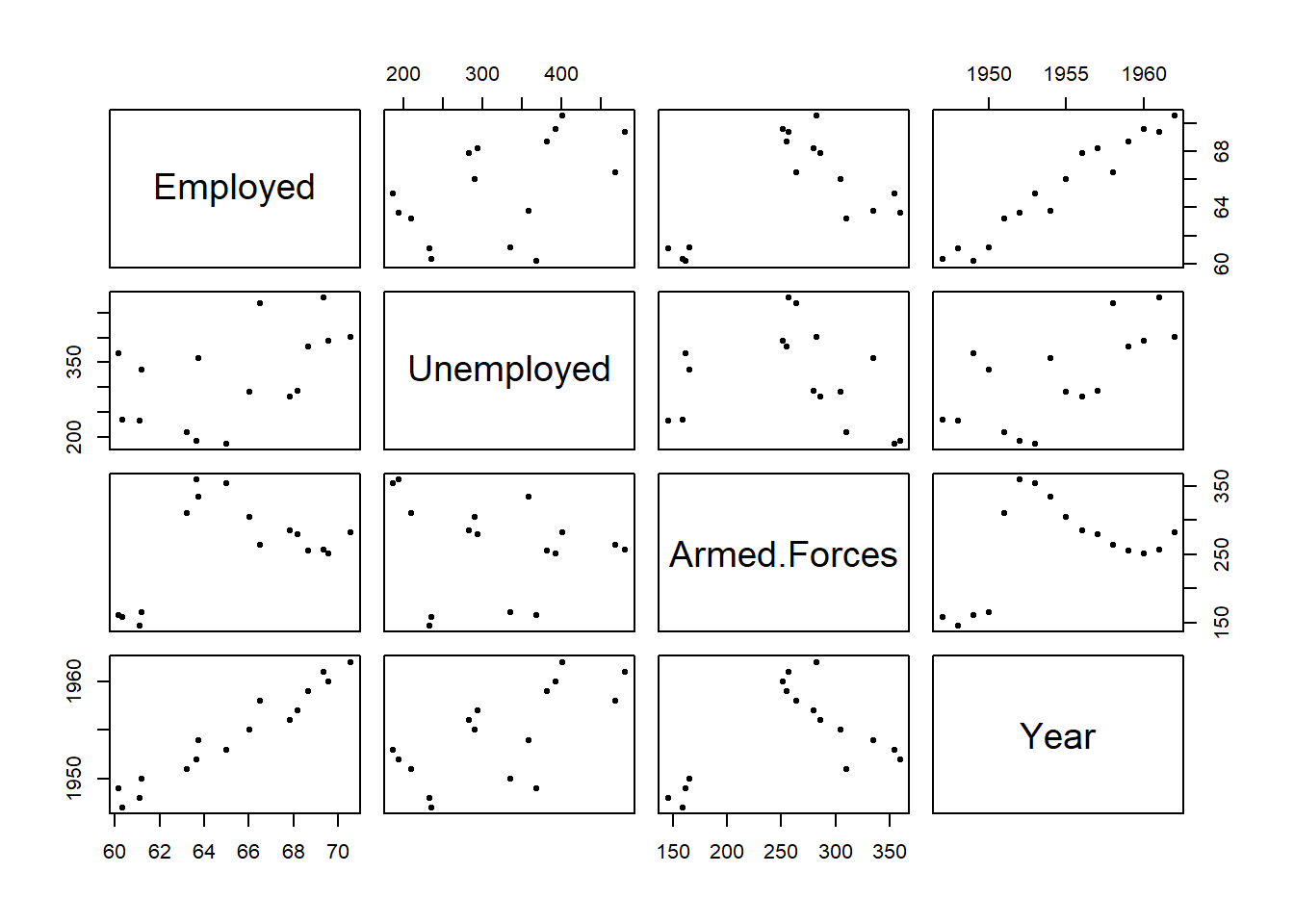

Luego lo que se debe hacer es ajustar el modelo así.

mod <- lm(Employed ~ Unemployed + Armed.Forces + Year, data=longley)

library(broom)
tidy(mod, quick=TRUE)

## # A tibble: 4 × 5
##   term            estimate std.error statistic  p.value
##   <chr>              <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)  -1797.       68.6        -26.2  5.89e-12
## 2 Unemployed      -0.0147    0.00167     -8.79 1.41e- 6
## 3 Armed.Forces    -0.00772   0.00184     -4.20 1.22e- 3
## 4 Year             0.956     0.0355      26.9  4.24e-12

De la tabla anterior tenemos que el modelo ajustado es el siguiente:

\[ \widehat{\text{Employed}} = -1797.22 - 0.01 \, \text{Unemployed} - 0.01 \, \text{Armed.Forces} + 0.96 \, \text{Year} \]

Podríamos usar la expresión anterior y reemplazar los valores de año, desempleados y personas en fuerzas armadas, dadas arriba, para calcular \(E(Employed|\boldsymbol{X}=\boldsymbol{x}_0)\). Sin embargo, aquí lo vamos a realizar usando la función predict.

Ahora vamos construir un nuevo marco de datos con la información de las covariables, usando los mismos nombres y los mismos tipos de variables (cuali o cuanti) que en el conjunto de datos con el cual se entrenó el modelo.

nuevo <- data.frame(Year=c(1963, 1964),
                    Unemployed=c(420, 430),
                    Armed.Forces=c(270, 250))
nuevo

##   Year Unemployed Armed.Forces
## 1 1963        420          270
## 2 1964        430          250

Ahora ya podemos usar la función predict para obtener lo solicitado.

predict(object=mod, newdata=nuevo)

##        1        2 
## 71.89467 72.85853

De la salida anterior tenemos los valores de \(\widehat{Employed}\).

¿Qué sucede si en el nuevo marco de datos anterior las variables se llaman diferente a las variables conjunto de datos de entrenamiento?

Error, nos sale un error. No se le ocurra usar nombres diferentes.

Intervalo de confianza para la respuesta media \(E(Y|x_0)\)

En regresión lineal simple, Si \(\hat{\mu}_{Y|x_0}\) es la media estimada para la variable respuesta cuando \(X=x_0\), entonces un IC del \((1−\alpha⁄2)\)×100% para \(E(Y|x_0)\) está dado por:

\[ \hat{\mu}_{Y|x_0} \pm t_{\alpha / 2, n - p} \, \sqrt{MS_{Res} \left(\frac{1}{n} + \frac{(x_0 - \bar{x})^2}{\sum(x_i - \bar{x})^2} \right)} \]

Intervalo de confianza para la predicción de nuevas observaciones

En regresión lineal simple, si \(\hat{Y}_0\) es el valor estimado para la variable respuesta cuando \(X=x_0\), entonces un IC del \((1−\alpha⁄2)\)×100% para \(Y_0\) está dado por:

\[ \hat{Y}_0 \pm t_{\alpha / 2, n - p} \, \sqrt{MS_{Res} \left(1 +\frac{1}{n} + \frac{(x_0 - \bar{x})^2}{\sum(x_i - \bar{x})^2} \right)} \]

Ejemplo

Como ilustración vamos a usar los datos del ejemplo 2.1 del libro de Montgomery, Peck and Vining (2003). En el ejemplo 2.1 los autores ajustan un modelo de regresión lineal simple para explicar la Resistencia de una soldadura en función de la Edad de la soldadura.

El objetivo es obtener:

IC del 95% para \(E(Y|x_0)\) cuando \(x_0=13\) semanas.
IC del 95% para \(E(Y|x_0)\) cuando \(x_0=2\) semanas.
IC del 90% para \(\hat{Y}_0\) cuando \(x_0=10\) semanas.
Crear el diagrama de dispersión agregando las líneas de los IC de 95% para \(E(Y|x_0)\) y \(\hat{Y}_0\).

Solución

Lo primero es disponer los datos.

file <- "https://raw.githubusercontent.com/fhernanb/datos/master/propelente"
datos <- read.table(file=file, header=TRUE)
head(datos)

##   Resistencia  Edad
## 1     2158.70 15.50
## 2     1678.15 23.75
## 3     2316.00  8.00
## 4     2061.30 17.00
## 5     2207.50  5.50
## 6     1708.30 19.00

Luego se ajusta el modelo.

mod1 <- lm(Resistencia ~ Edad, data=datos)

Ahora vamos a explorar la tabla de resumen del modelo anterior.

summary(mod1)

## 
## Call:
## lm(formula = Resistencia ~ Edad, data = datos)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -215.98  -50.68   28.74   66.61  106.76 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 2627.822     44.184   59.48  < 2e-16 ***
## Edad         -37.154      2.889  -12.86 1.64e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 96.11 on 18 degrees of freedom
## Multiple R-squared:  0.9018, Adjusted R-squared:  0.8964 
## F-statistic: 165.4 on 1 and 18 DF,  p-value: 1.643e-10

En la tabla anterior está toda la información para hacer las estimaciones manualmente pero aquí lo vamos a realizar de forma computacional.

Para obtener el IC del 95% para \(E(Y|x_0)\) para \(x_0=13\) y \(x_0=2\) se usa el siguiente código.

new_dt <- data.frame(Edad=c(13, 2))
predict(object=mod1, newdata=new_dt, interval="confidence", level=0.95)

##        fit      lwr      upr
## 1 2144.826 2099.623 2190.028
## 2 2553.515 2471.083 2635.947

Para obtener el IC del 90% para \(\hat{Y}_0\) cuando \(x_0=10\) semanas se usa el siguiente código.

new_dt <- data.frame(Edad=10)
predict(object=mod1, newdata=new_dt, interval="prediction", level=0.90)

##        fit      lwr      upr
## 1 2256.286 2084.688 2427.885

Observe que en el primer caso se usó interval="confidence" mientras que en el segundo se usó interval="prediction".

Ahora vamos a obtener todos los IC \(\hat{Y}_0\) y los vamos a almacenar en el objeto future_y que luego luego vamos a agregar al marco de datos original.

future_y <- predict(object=mod1, interval="prediction", level=0.95)
nuevos_datos <- cbind(datos, future_y)

Con el código mostrado a continuación se construye el diagrama de dispersión y se agrega la línea de regresión (en azul) y los IC para \(E(Y|x_0)\) (en rosado) por medio de geom_smooth. Los IC para \(\hat{Y}_0\) (en rojo) se agregan por medio de geom_line.

library(ggplot2)
ggplot(nuevos_datos, aes(x=Edad, y=Resistencia))+
    geom_point() +
    geom_line(aes(y=lwr), color="red", linetype="dashed") +
    geom_line(aes(y=upr), color="red", linetype="dashed") +
    geom_smooth(method=lm, formula=y~x, se=TRUE, level=0.95, col='blue', fill='pink2') +
    theme_light()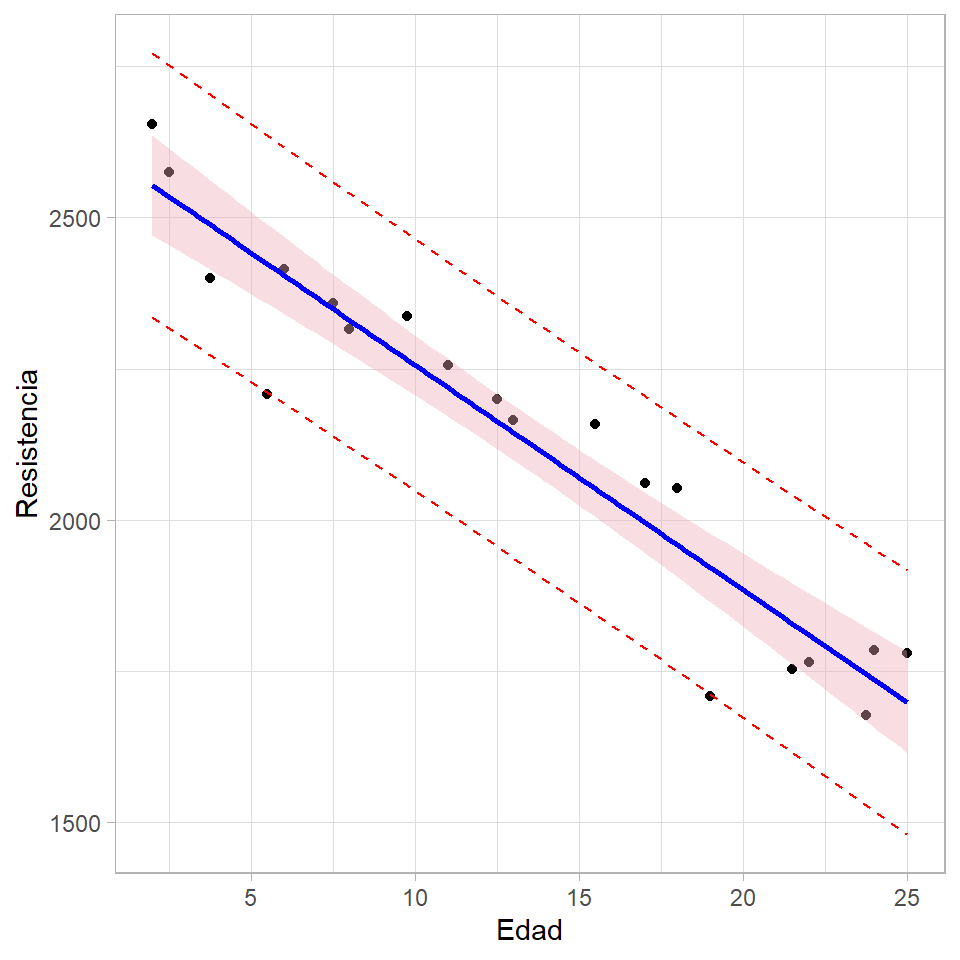

De la figura anterior se observa claramente que los IC para \(\hat{Y}_0\) son siempre más anchos que los IC para \(E(Y|x_0)\).

4 Predicción

Función predict

Ejemplo

Intervalo de confianza para la respuesta media \(E(Y|x_0)\)

Intervalo de confianza para la predicción de nuevas observaciones

Ejemplo

Función `predict`