20 Algebra matricial con R

En este capítulo se muestran algunas funciones útiles para álgebra lineal con R.

Matrices

Una matriz es un arreglo bidimensional (filas y columna) de números.

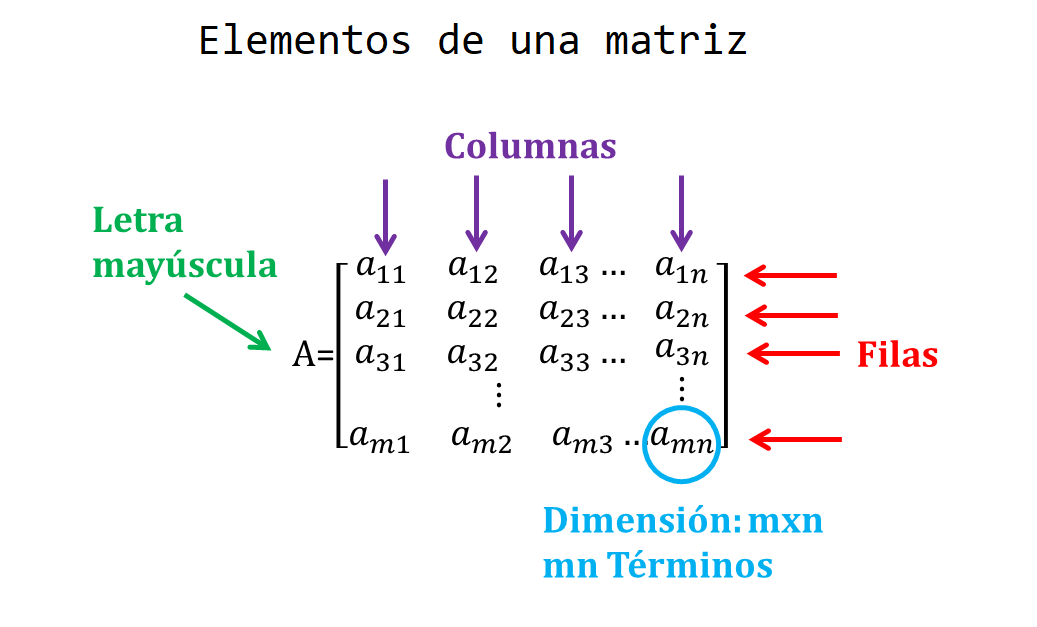
La función para crear una matriz es matrix. A continuación se muestran los argumentos de la función.

matrix(data=NA, nrow=1, ncol=1, byrow=FALSE, dimnames=NULL)

Ejemplo

Crear en R la matriz \(M\) siguiente.

\[ M = \begin{pmatrix} 1 & 2 \\ 1 & 5 \end{pmatrix} \]

Solución

Para crear la matriz podemos usar el siguiente código.

M <- matrix(c(1, 2,
              1, 5), nrow=2, byrow=TRUE)
M

##      [,1] [,2]
## [1,]    1    2
## [2,]    1    5

Operaciones básicas sobre una matriz

En la siguiente tabla se listan algunas de las funciones que se pueden utilizar sobre matrices. Los objetos A y B son matrices mientras que los objetos x y b son vectores.

Operador	Descripción
`A * B`	Element-wise multiplication
`A %*% B`	Matrix multiplication
`A %o% B`	Outer product. \(AB^\top\).
`t(A)`	Transpose
`diag(x)`	Creates diagonal matrix with elements of x in the principal diagonal
`diag(A)`	Returns a vector containing the elements of the principal diagonal
`diag(k)`	If `k` is a scalar, this creates a \(k \times k\) identity matrix. Go figure.
`solve(A, b)`	Returns vector x in the equation b = Ax (i.e., A-1b)
`solve(A)`	Inverse of A where A is a square matrix.
`ginv(A)`	Moore-Penrose Generalized Inverse of A.
`ginv(A)`	requires loading the MASS package.
`cbind(A,B,...)`	Combine matrices(vectors) horizontally. Returns a matrix.
`rbind(A,B,...)`	Combine matrices(vectors) vertically. Returns a matrix.
`rowMeans(A)`	Returns vector of row means.
`rowSums(A)`	Returns vector of row sums.
`colMeans(A)`	Returns vector of column means.
`colSums(A)`	Returns vector of column sums.

Rango de una matriz

El rango de una matriz es el número máximo de columnas (filas respectivamente) que son linealmente independientes.

Ejemplo

Calcular el rango de la matriz \(M\) siguiente.

\[ M = \begin{pmatrix} 1 & 2 & 5 \\ 1 & 5 & 2 \\ 1 & 4 & 7 \end{pmatrix} \]

Solución

Lo primero es crear la matriz \(M\).

M <- matrix(c(1, 2, 5,
              1, 5, 2,
              1, 4, 7), ncol=3, byrow=TRUE)
M

##      [,1] [,2] [,3]
## [1,]    1    2    5
## [2,]    1    5    2
## [3,]    1    4    7

Una forma de obtener el rango es por medio de la función qr que hace una descomposición QR de la matriz.

qr(M)$rank

## [1] 3

De la salida anterior vemos que el rango de \(M\) es 3, eso quiere decir que el número máximo de columnas linealmente independientes es 3.

Otra forma para obtener el rango de la matriz es por medio de la función rankMatrix del paquete Matrix (Bates, Maechler, and Jagan 2024) así:

library(Matrix)
rankMatrix(M)[1]

## [1] 3

Ejemplo

Calcular el rango de la matriz \(N\) siguiente.

\[ N = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 5 & 6 \\ 1 & 7 & 8 \end{pmatrix} \]

Solución

Lo primero es crear la matriz \(N\).

N <- matrix(c(1, 2, 3,
              1, 5, 6,
              1, 7, 8), ncol=3, byrow=TRUE)
N

##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    1    5    6
## [3,]    1    7    8

Al mirar con calma las columnas de la matriz se observa un detalle, la tercera columna de \(N\) se obtiene al sumar la primera y segunda columna de \(N\), eso significa que la tercera columna es combinación lineal de las dos primeras. Vamos a calcular el rango de \(N\).

qr(N)$rank

## [1] 2

El valor de 2 obtenido no nos sorprende porque ya habíamos detectado que la tercera columna es combinación lineal de las dos primeras.

References

Bates, Douglas, Martin Maechler, and Mikael Jagan. 2024. Matrix: Sparse and Dense Matrix Classes and Methods. https://Matrix.R-forge.R-project.org.