12 Pruebas de Homocedasticidad
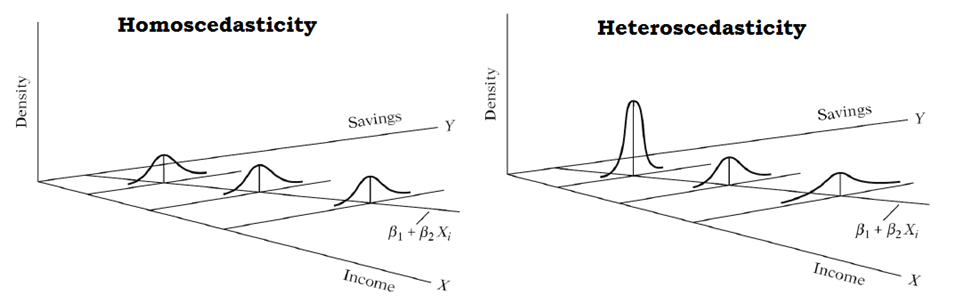
En este capítulo se presentan varias pruebas para explorar si se cumple el supuesto de homocedasticidad de los errores en regresión lineal.
En las prueba mostradas a continuación se estudian las siguientes hipótesis.
\[\begin{align*} H_0 &: \text{los errores tienen varianza constante.} \\ H_1 &: \text{los errores no tienen varianza constante.} \end{align*}\]
Breusch-Pagan Test
Esta prueba fue propuesta por Breusch and Pagan (1979) y consiste en ajustar un modelo de regresión lineal con variable respuesta dada por residuales del modelo original al cuadrado \(e_i^2\) y como covariables las variables del modelo original.
Por ejemplo, si se tienen \(k=2\) covariables para explicar a \(Y\), entonces el modelo de regresión para estudiar la homocedasticidad es:
\[ \hat{e}_i^2 = \delta_0 + \delta_1 x_1 + \delta_2 x_2 + u \]
Si se concluye que \(\delta_1=\delta_2=0\), significa que los residuales no son función de las covariables del modelo. El estadístico en esta prueba está dado por \(n \times R^2\) y bajo la hipótesis nula verdadera, el estadístico tiene distribución \(\chi^2_k\).
La función bptest del paquete lmtest Hothorn et al. (2022) implementa esta prueba.
Ejemplo
Simule un conjunto de datos donde se viole la hipótesis de varianza constante (de los \(e_i\) o de las \(y_i\)) y aplique las pruebas de hipótesis para ver si son capaces de detectar la violación del supuesto de homocedasticidad.
Solución
En el código mostrado a continuación se simulan observaciones en las cuales la varianza de \(e_i\) no es constante ya que para generar los datos se usa la instrucción ei <- rnorm(n=n, sd=x2), es decir que la varianza depende de la variable \(x_2\).
gen_data <- function(n) {
x1 <- rpois(n, lambda=5)
x2 <- rbinom(n, size=6, prob=0.4)
ei <- rnorm(n=n, sd=x2)
y <- -3 + 2 * x1 + 4 * x2 + ei
data.frame(y, x1, x2)
}
n <- 200
datos <- gen_data(n=n)
mod <- lm(y ~ x1 + x2, data=datos) # Modelo de interesVamos a aplicar la prueba de forma manual.
ei <- resid(mod)
fit <- lm(ei^2 ~ x1 + x2, data=datos) # Modelando ei^2 ~ x1 + x2
R2 <- summary(fit)$r.squared
k <- 2
estadistico <- n * R2
valorP <- pchisq(q=estadistico, df=k, lower.tail=FALSE)
cbind(estadistico, valorP)## estadistico valorP
## [1,] 29.23532 4.483652e-07Vamos a aplicar la prueba de forma automática con la función bptest.
##
## studentized Breusch-Pagan test
##
## data: mod
## BP = 29.235, df = 2, p-value = 4.484e-07De la salida anterior se observa que el valor-P es menor que el nivel de significancia usual de 5%, por lo tanto, hay evidencias para decir que no se cumple la homocedasticidad de los \(e_i\).
White test
El test de Breusch-Pagan sólo detecta formas lineales de heterocedasticidad. Para resolverlo, el test de White, propuesto por White (1980), permite contrastar no linealidades utilizando los cuadrados y los productos cruzados de todos los regresores. Si \(k=2\) el test de White crea el siguiente modelo de regresión:
\[ \hat{e}_i^2 = \delta_0 + \delta_1 x_1 + \delta_2 x_2 + \delta_3 x_1 x_2 + \delta_4 x_1^2 + \delta_5 x_2^2 + u \]
Este test se puede implementar por medio de la función bptest pero especificando los términos no lineales de la expresión anterior.
Ejemplo
Aplicar White test para los datos simulados del ejemplo anterior.
Solución
Para aplicar el test se usa el argumento varformula y se escribe la fórmula con los términos no lineales \(\delta_3 x_1 x_2 + \delta_4 x_1^2 + \delta_5 x_2^2\), los términos lineales están por defecto.
##
## studentized Breusch-Pagan test
##
## data: mod
## BP = 35.551, df = 5, p-value = 1.168e-06Como el valor-P es pequeño entonces hay evidencias para rechazar la hipótesis de homocedasticidad.
La prueba se puede también realizar de forma manual, a continuación se muestra el procedimiento.
fit <- lm(resid(mod)^2 ~ x1 + x2 + x1 * x2 + I(x1^2) + I(x2^2), data=datos)
R2 <- summary(fit)$r.squared
estadistico <- n * R2
valorP <- pchisq(q=estadistico, df=5, lower.tail=FALSE)
cbind(estadistico, valorP)## estadistico valorP
## [1,] 35.55051 1.168159e-06Score test for nonconstant error variance
Esta prueba sirve para estudiar la hipótesis nula de varianza constante de los errores frente a la hipótesis alternativa de que la varianza de los errores cambia con el nivel de la respuesta o con alguna combinación lineal de los predictores.
La función ncvTest del paquete car John Fox, Weisberg, and Price (2023) implementa esta prueba.