6 Diagnósticos
En este capítulo se presentan varias herramientas útiles para hacer diagnósticos de un modelo ajustado.
Residuales
Los residuales en los modelos de regresión nos ayuda a:
- determinar qué tan bien el modelo explica el patrón de los datos,
- verificar el cumplimiento de los supuestos del modelo.
A continuación se muestran los diferentes tipos de residuales que se pueden definir para un modelo de regresión.

La cantidad \(w_i\) corresponde al peso o importancia de cada observación en el modelo, por defecto es 1.
La cantidad \(h_{ii}\) se llama leverage y corresponde al elemento \(i\) de la diagonal de la matriz sombrero o hat \(\boldsymbol{H} = \boldsymbol{X}(\boldsymbol{X}\boldsymbol{X}^\top)^{-1}\boldsymbol{X}^\top\).
La varianza \(\hat{\sigma}_{(i)}^{2}\) es la varianza estimada al NO tener en cuenta la observación \(i\)-ésima. La cantidad \(\hat{y}_{(i)}\) es la estimación de la \(i\)-ésima observación usando un modelo en el cual la observación \(i\)-ésima NO participó.
Para obtener los residuales arriba definidos tenemos las siguientes funciones:
Supuestos
Los supuestos en un modelo de regresión se pueden escribir de dos formas:
Forma I
- Los errores \(e_i\) tienen distribución normal.
- Los errores \(e_i\) tienen media cero.
- Los errores \(e_i\) tiene varianza constante.
- Los errores \(e_i\) no están correlacionados.
Forma II
- La respuesta \(y\) tiene distribución normal.
- La varianza de la respuesta \(y\) es constante.
- Las observaciones son independientes \(y\).
- Relación lineal entre la variable respuesta y las covariables.
Ambos conjuntos de supuestos son equivalentes, la forma I está dirigida hacia los \(e_i\) mientras que en la forma II está dirigida hacia los \(y_i\).
Chequeando normalidad de los errores \(e_i\)
Para estudiar si lo errores \(e_i\) tienen una distribución aproximadamente normal se construyen los residuales estandarizados \(d_i\). Una vez calculados los \(d_i\) se construye un gráfico de normalidad o qqplot usando la función qqnorm, el resultado es un gráfico similar al mostrado a continuación.
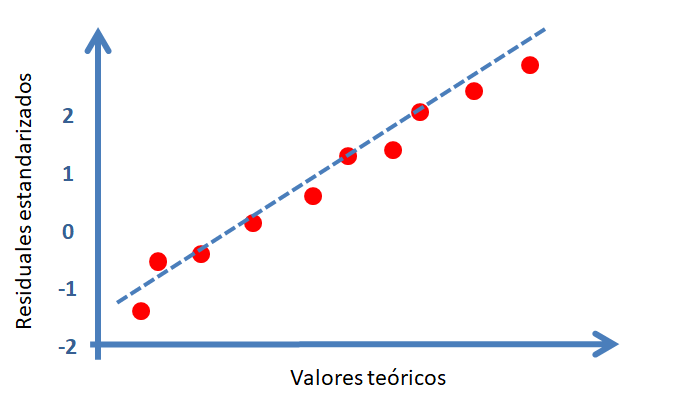
En la siguiente figura se muestran los diferentes patrones que se pueden encontrar en el gráfico de normalidad para \(d_i\). Para que se cumpla el supuesto de normalidad de los errores \(e_i\) se necesita que los \(d_i\) estén lo más alineados con la recta de referencia, alejamientos severos de esta recta significa que se viola el supuesto de normalidad de \(e_i\).
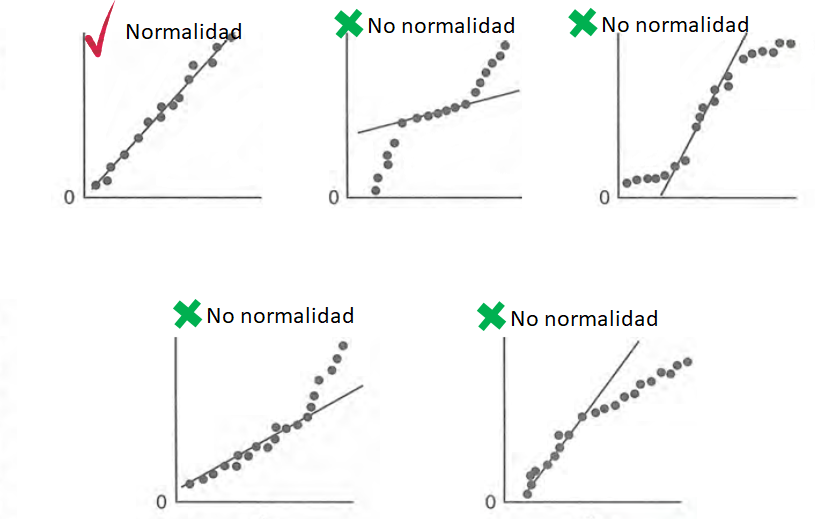
Chequeando si errores \(e_i\) con media cero
Para determinar si los errores \(e_i\) tienen una media cerca al valor de cero se puede usar la función mean sobre los residuales.
Chequeando si los errores \(e_i\) tiene varianza constante
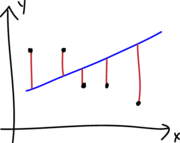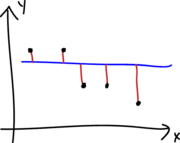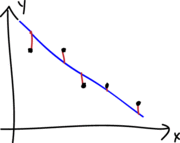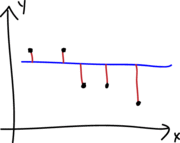
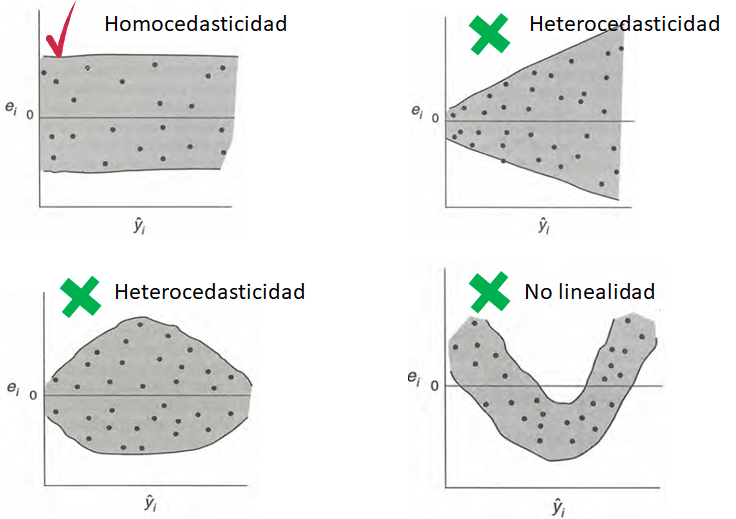
En la siguiente figura se muestra el caso de varianza \(\sigma^2\) constante u homocedasticidad y el caso de varianza \(\sigma^2\) no constante o heterocedasticidad. La homocedasticidad es el supuesto exigido en modelos de regresión.
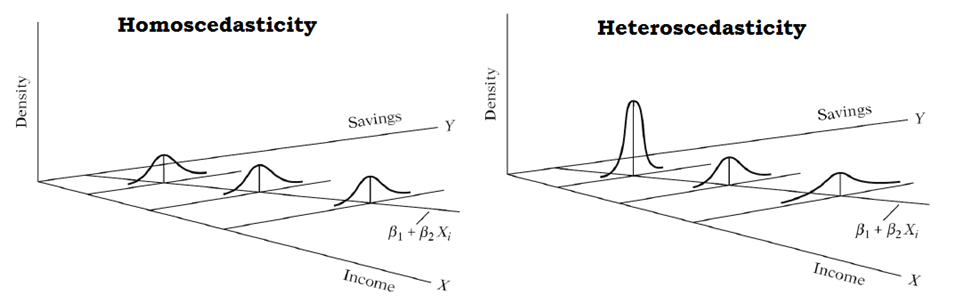
Para chequear si los errores \(e_i\) tiene varianza constante se construye un gráfico de \(e_i\) versus \(\hat{\mu}\), un gráfico similar al mostrado a continuación.
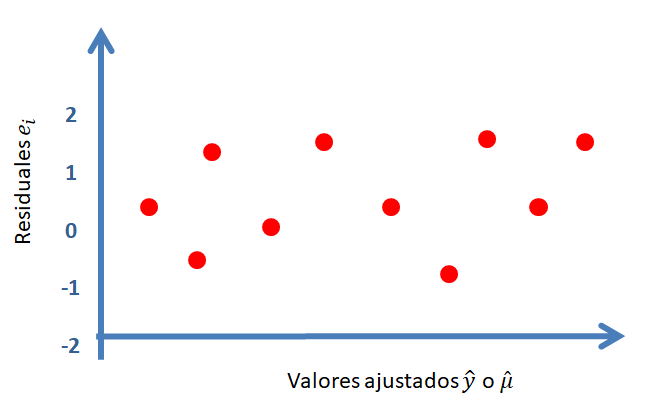
En la siguiente figura se muestran los diferentes patrones que se pueden encontrar en el gráfico de \(e_i\) versus \(\hat{\mu}\). Para que se cumpla el supuesto de homocedasticidad se necesita que los puntos se ubiquen como una nube de puntos sin ningún patrón claro. Cualquier patrón que se observe es evidencia de que no se cumple el supuesto de homocedasticidad.
Una analogía útil para recordar si se cumple la homocedasticidad es que el gráfico de \(e_i\) versus \(\hat{\mu}\) tenga una apariencia como la mostrada en la siguiente figura.

Otro gráfico útil para chequear el supuesto de homocedasticidad es dibujar un diagrama de dispersión de \(\sqrt{|r_i|}\) versus \(\hat{\mu}\), un gráfico similar al mostrado a continuación.
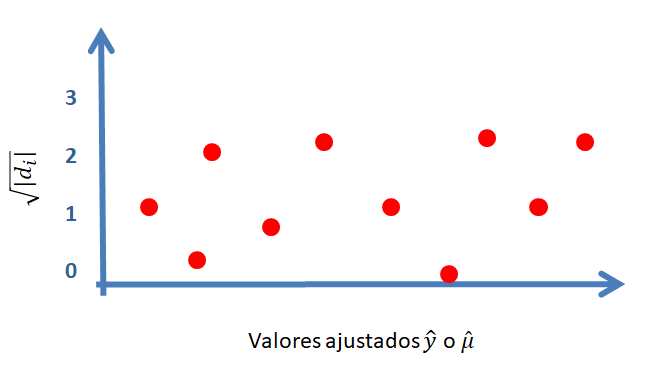
Al igual que en el gráfico de \(e_i\) versus \(\hat{\mu}\), se espera que no existan patrones claros en la nube de puntos.
Chequeando si errores \(e_i\) no están correlacionados
Para estudiar esta situación se debe tener la historia de los errores, es decir, el orden en que las observaciones fueron tomadas. Usando es información se puede dibujar un diagrama de dispersión del residual versus tiempo, un gráfico similar al mostrado a continuación.
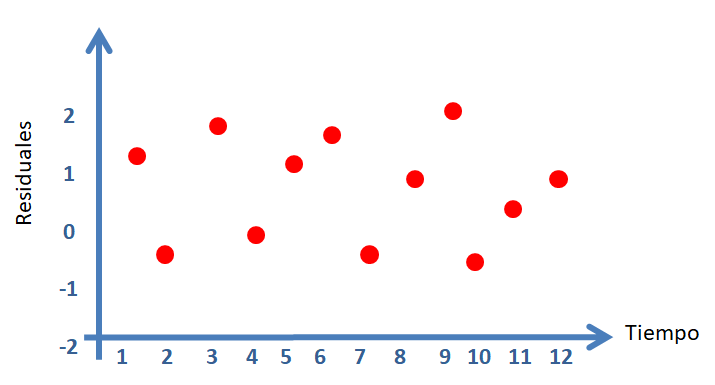
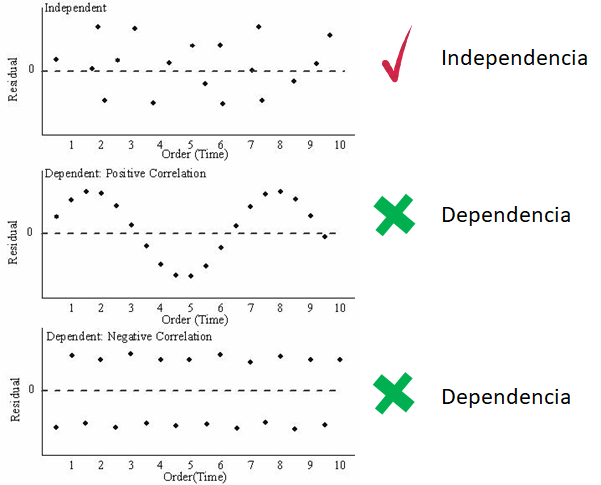
En la siguiente figura se muestran los diferentes patrones que se pueden encontrar en el gráfico de \(e_i\) versus el tiempo. Para que se cumpla el supuesto de independencia se espera que los puntos se ubiquen como una nube de puntos sin ningún patrón claro.
Ejemplo
En este ejemplo vamos a simular 1000 observaciones del siguiente modelo y luego vamos a realizar el análisis de residuales para saber si el modelo fue bien ajustado.
\[\begin{align*} y_i &\sim N(\mu_i, \sigma^2) \\ \mu_i &= 4 - 6 x_i \\ x_i &\sim U(-5, 6) \\ \sigma^2 &= 16 \end{align*}\]
Solución
Lo primero que se debe hacer es simular los datos y ajustar el modelo.
gen_dat <- function(n) {
varianza <- 16
x <- runif(n=n, min=-5, max=6)
media <- 4 - 6 * x
y <- rnorm(n=n, mean=media, sd=sqrt(varianza))
marco_datos <- data.frame(y=y, x=x)
return(marco_datos)
}
datos <- gen_dat(n=1000)
mod <- lm(y ~ x, data=datos)Luego se pueden obtener los gráficos de residuales de la siguiente manera.
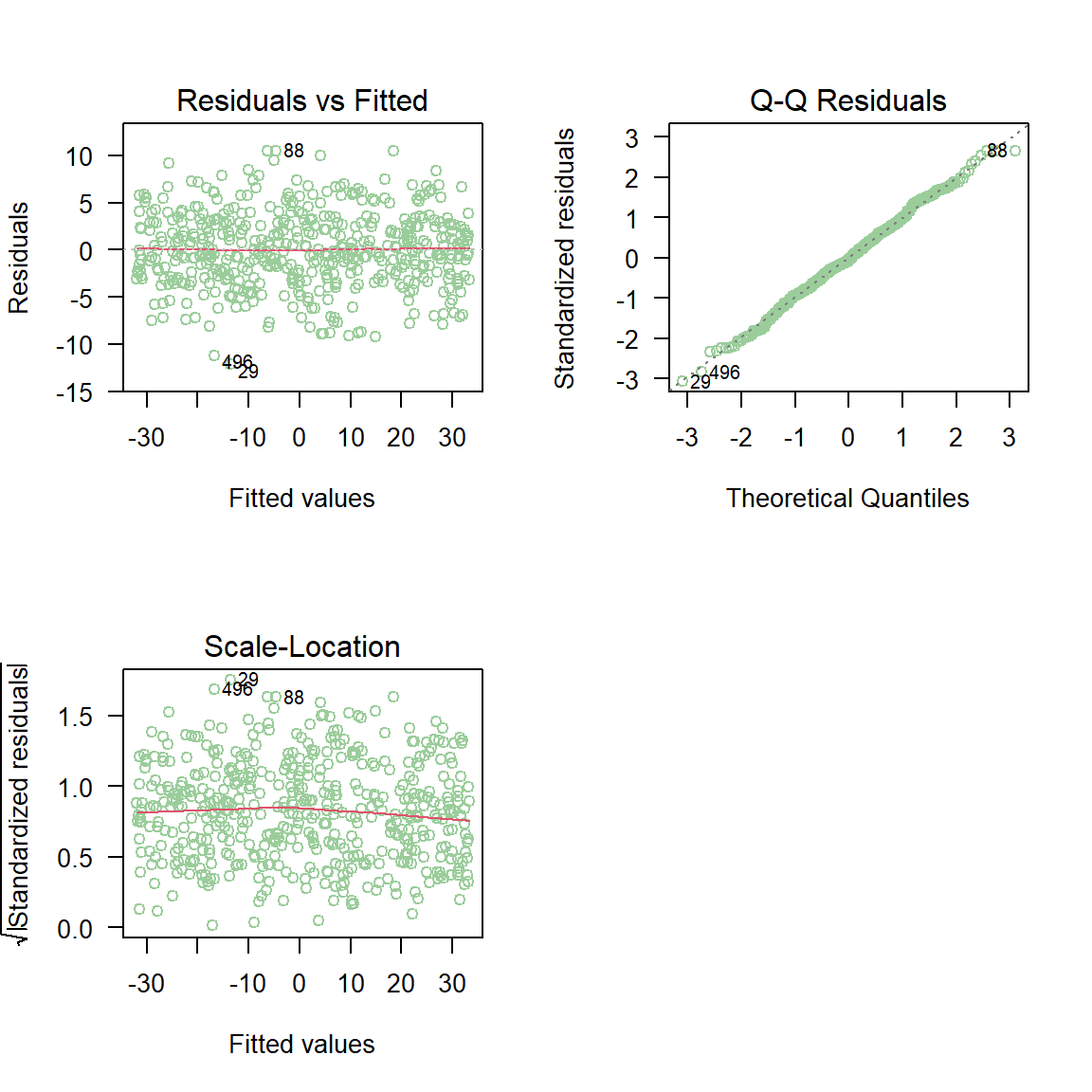
En la figura anterior se observa que los puntos del gráfico de normalidad de los residuales estandarizados \(d_i\) están muy cerca de la línea de referencia. Los diagramas de dispersión entre los residuales versus \(\hat{\mu}\) no muestran ninguna anomalía. Por estas razones podemos asumir que los supuestos del modelo se cumplen.
Reto para el lector
Use la información del ejemplo anterior y viole alguno de los supuestos dentro de la función gen_dat o al momento de ajustar el modelo con lm. Luego construya los gráficos de residuales y compruebe que los gráficos le indicarán las anomalías que usted introdujo al modelo.
Matriz sombrero o hat
La matriz sombrero o matriz Hat se define así:
\[ \boldsymbol{H} = \boldsymbol{X}(\boldsymbol{X}\boldsymbol{X}^\top)^{-1}\boldsymbol{X}^\top \]
Esta matriz contiene en su diagonal las distancias relativas desde el centroide de los datos hasta cada uno de los puntos. En la siguiente figura se ilustra el concepto de distancia relativa entre el centroide (color rojo) de las variables explicativas y cada uno de los puntos para un caso con tres variables explicativas \(x_1\), \(x_2\) y \(x_3\).
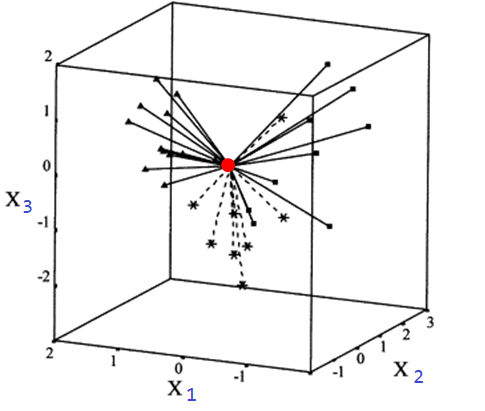
La cantidad \(h_{ii}\) se llama leverage y corresponde al elemento \(i\) de la diagonal de la matriz sombrero \(\boldsymbol{H}\). Los valores de \(h_{ii}\) siempre están entre 0 y 1. Si la observación \(i\)-ésima tiene un valor grande de \(h_{ii}\) significa que ella tiene valores inusuales de \(\boldsymbol{x}_i\), mientras que valores pequeños de \(h_{ii}\) significa que la observación se encuentra cerca del centroide de los datos.
¿Para qué se usan los \(h_{ii}\) en la práctica?
En el siguiente apartado se explicará el uso de los \(h_{ii}\).
¿Qué es extrapolación oculta?
Suponga tenemos un modelo de regresión una variable respuesta y dos covariables \(x_1\) y \(x_2\). En la siguiente figura se ilustra los posibles datos desde una vista superior (sin ver los valores de \(y\)). Esa elipse o forma se llama Regressor Variable Hull (RVH) o cascarón de los datos.
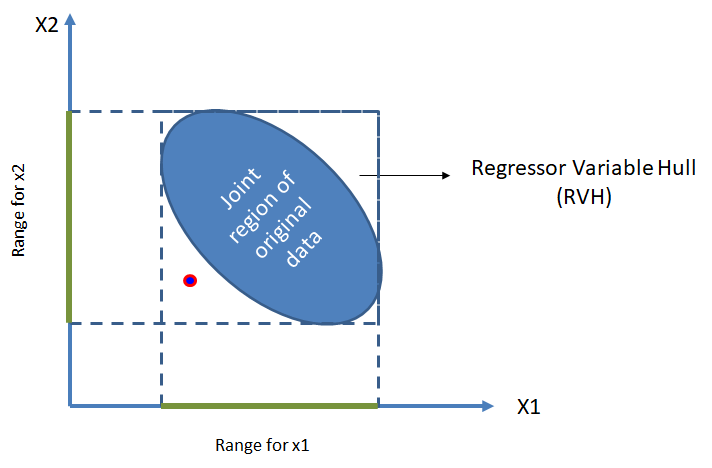
Una vez se tenga el modelo ajustado podríamos usar valores de \(x_1\) y \(x_2\) para estimar la media de \(y\). Lo ideal es usar el modelo para predecir la media de \(y\) con valores de \(x_1\) y \(x_2\) que se encuentren dentro del cascarón.
Si tratamos de estimar la media de \(y\) para valores de las covariables fuera del cascarón, como en el caso del punto rojo, no podemos garantizar que el modelo tenga un buen desempeño debido a que el modelo no se entrenó con ese tipo de ejemplos.
El problema de extrapolación oculta se presenta cuando tratamos de predecir información de \(y\) con covariables fuera del cascarón. La extrapolación oculta es fácil de identificarla cuando sólo se tiene dos covariables, pero, ¿cómo saber si se está haciendo extrapolación oculta cuando se tienen varias covariables. Supongamos que queremos saber si el vector de covariables \(\boldsymbol{x}_0=(x_1, x_2, \ldots, x_p)^\top\) está o no dentro del cascarón, dicho de otra manera, ¿se cometería extrapolación oculta usando \(\boldsymbol{x}_0\)?. Los pasos para determinar si \(\boldsymbol{x}_0\) está o no dentro del cascarón son:
- Calcular la matriz \(\boldsymbol{H}\).
- Obtener los valores \(h_{ii}\) de la matriz \(\boldsymbol{H}\).
- Identificar \(h_{max} = max\{h_{11}, h_{22}, \ldots, h_{nn}\}\).
- Calcular \(h_{00} = \boldsymbol{x}_0 (\boldsymbol{X}^\top \boldsymbol{X})^{-1} \boldsymbol{x}_0^\top\).
- Si \(h_{00} > h_{max}\) el punto \(\boldsymbol{x}_0\) está fuera del cascarón y se podría estár cometiendo extrapolación oculta.
Los valores \(h_{ii}\) se pueden obtener al calcular la matriz \(\boldsymbol{H}\). Otra forma de obtener los \(h_{ii}\) es ajustando el modelo de regresión y luego usando la función hatvalues(model) o lm.influence(model).
Ejemplo
Calcular los valores \(h_{ii}\) para un modelo de regresión y ~ x + z con los siguientes datos.
Solución
A seguir se muestran las tres formas para obtener los valores \(h_{ii}\).
## [,1] [,2] [,3] [,4]
## [1,] 8.333333e-01 3.333333e-01 -3.552714e-15 -0.1666667
## [2,] 3.333333e-01 3.333333e-01 -9.992007e-16 0.3333333
## [3,] -2.664535e-15 -1.110223e-15 1.000000e+00 0.0000000
## [4,] -1.666667e-01 3.333333e-01 -1.332268e-15 0.8333333## [1] 0.8333333 0.3333333 1.0000000 0.8333333## 1 2 3 4
## 0.8333333 0.3333333 1.0000000 0.8333333## 1 2 3 4
## 0.8333333 0.3333333 1.0000000 0.8333333Reto para el lector
Use la información del ejemplo anterior y determine si la observación con valores de \(x=4\) y \(z=1\) está o no dentro del cascarón de los datos, en otras palabras, determine si se podría cometer extrapolación oculta al usar el modelo ajustado con \(x=4\) y \(z=1\).
Gráficos de residuales usando car
El paquete car (Fox, Weisberg, and Price 2020) tiene unas funciones para crear otro tipo de gráficos de residuales y que son útiles para identificar posibles anomalías en el modelo ajustado. A continuación se muestra la estructura de esas funciones.
Ejemplo
Este ejemplo corresponde al ejemplo mostrado en el capítulo 6 de Fox and Weisberg (2011).
En este ejemplo se desea ajustar un modelo de regresión para explicar la media de la variable prestige en función de las variables education, income y type, usando la base de datos Prestige del paquete car (Fox, Weisberg, and Price 2020).

## 'data.frame': 102 obs. of 6 variables:
## $ education: num 13.1 12.3 12.8 11.4 14.6 ...
## $ income : int 12351 25879 9271 8865 8403 11030 8258 14163 11377 11023 ...
## $ women : num 11.16 4.02 15.7 9.11 11.68 ...
## $ prestige : num 68.8 69.1 63.4 56.8 73.5 77.6 72.6 78.1 73.1 68.8 ...
## $ census : int 1113 1130 1171 1175 2111 2113 2133 2141 2143 2153 ...
## $ type : Factor w/ 3 levels "bc","prof","wc": 2 2 2 2 2 2 2 2 2 2 ...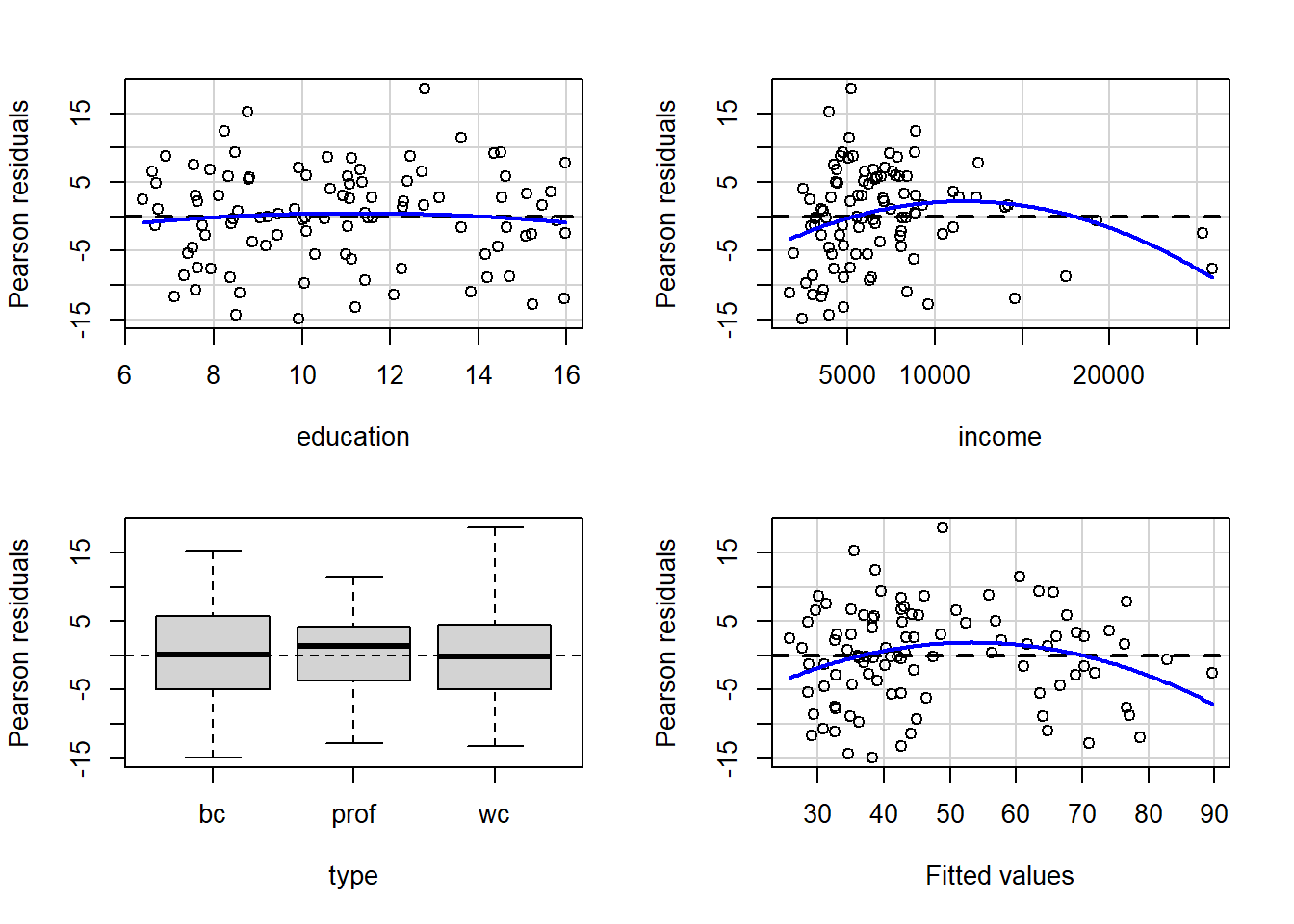
## Test stat Pr(>|Test stat|)
## education -0.6836 0.495942
## income -2.8865 0.004854 **
## type
## Tukey test -2.6104 0.009043 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## Warning in mmps(...): Interactions and/or factors skipped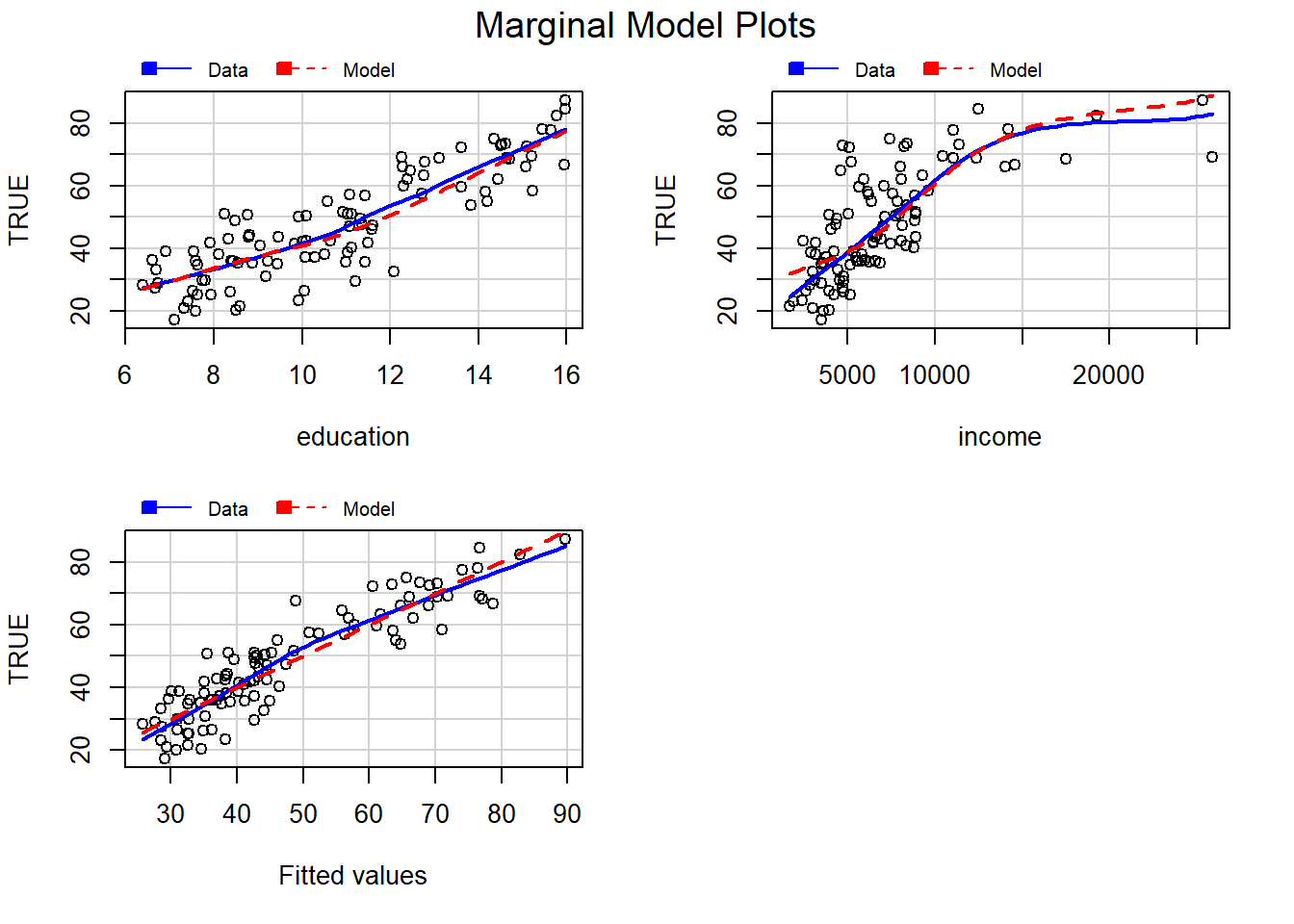
References
Fox, John, Sanford Weisberg, and Brad Price. 2020. Car: Companion to Applied Regression. https://CRAN.R-project.org/package=car.