28 Intervalos de confianza

En este capítulo vamos mostrar como se pueden obtener intervalos de confianza para los parámetros del modelo e intervalos de confianza para predicción.

28.1 Intervalos de confianza para los parámetros

En esta sección se mostrará cómo utilizar la función confint() para obtener intervalos de confianza para los elementos del vector de parámetros \(\boldsymbol{\Theta}\) de un modelo lineal generalizado mixto.

Ejemplo: modelo normal

En este ejemplo su usará la base de datos sleepstudy del paquete lme4 de Bates et al. (2025) sobre el tiempo de reacción promedio por día para un conjunto de individuos en un estudio de privación del sueño. La base de datos contiene la información sobre el tiempo de reacción promedio (Reaction), el número de días de privación del sueño (Days), donde el día 0 corresponde al día en el que los individuos tenían su cantidad normal de sueño, y el número del individuo (en total 18) sobre el que se realizó la observación (Subject). A partir del día 0, hubo una restricción en cada individuo a 3 horas de sueño por noche.

El objetivo es ajustar el siguiente modelo a los datos.

\[\begin{align*} Reaction_{ij} | b_0, b_1 &\sim N(\mu_{ij}, \sigma^2_{Reaction}) \\ \mu_{ij} &= \beta_0 + \beta_1 Days_{ij} + b_{0i} + b_{1i} Days_{ij} \\ \left ( \begin{matrix} b_{0} \\ b_{1} \end{matrix} \right ) &\sim N\left ( \left [ \begin{matrix} 0 \\ 0 \end{matrix} \right ], \left [ \begin{matrix} \sigma^2_{b0} & \sigma_{b01} \\ \sigma_{b01} & \sigma^2_{b1} \end{matrix} \right ] \right ) \end{align*}\]

Solución.

Lo primero que debemos hacer es ajustar el modelo usando el siguiente código.

library(lme4)

## Loading required package: Matrix

head(sleepstudy)

##   Reaction Days Subject
## 1 249.5600    0     308
## 2 258.7047    1     308
## 3 250.8006    2     308
## 4 321.4398    3     308
## 5 356.8519    4     308
## 6 414.6901    5     308

fit <- lmer(Reaction ~ Days + (Days | Subject), REML = TRUE, data = sleepstudy)

La tabla de resultados del modelo ajustado se muestra a continuación.

summary(fit)

## Linear mixed model fit by REML ['lmerMod']
## Formula: Reaction ~ Days + (Days | Subject)
##    Data: sleepstudy
## 
## REML criterion at convergence: 1743.6
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.9536 -0.4634  0.0231  0.4634  5.1793 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr
##  Subject  (Intercept) 612.10   24.741       
##           Days         35.07    5.922   0.07
##  Residual             654.94   25.592       
## Number of obs: 180, groups:  Subject, 18
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)  251.405      6.825  36.838
## Days          10.467      1.546   6.771
## 
## Correlation of Fixed Effects:
##      (Intr)
## Days -0.138

De la tabla anterior podemos ver que las estimaciones del vector de parámetros es

\[ \hat{\boldsymbol{\Theta}} = (\hat{\beta_0}=251.40, \hat{\beta_1}=10.47, \hat{\sigma}_{reaction}=25.59, \hat{\sigma}_{b0}=24.74, \hat{\sigma}_{b1}=5.92, \hat{\rho}_{b0b1}=0.07)^\top \]

Para obtener los intervalos de confianza podemos usar la función confint().

#### Calculate Wald CIs (Fastest Version) ####
ci.wald <- confint(fit, level=0.95)

## Computing profile confidence intervals ...

ci.wald

##                   2.5 %      97.5 %
## .sig01       14.3814379  37.7159918
## .sig02       -0.4815008   0.6849863
## .sig03        3.8011643   8.7533658
## .sigma       22.8982669  28.8579965
## (Intercept) 237.6806955 265.1295145
## Days          7.3586533  13.5759188

También es posible obtener los intervalos de confianza por el método boostrap así.

#### Calculate Bootstrapped CIs ####
ci.boot <- confint(fit, method = "boot", nsim = 1000)

## Computing bootstrap confidence intervals ...

## 
## 15 message(s): boundary (singular) fit: see help('isSingular')
## 6 warning(s): Model failed to converge with max|grad| = 0.00211214 (tol = 0.002, component 1) (and others)

ci.boot

##                   2.5 %      97.5 %
## .sig01       11.3506266  35.0783448
## .sig02       -0.5221701   0.9272534
## .sig03        3.4053626   8.2279565
## .sigma       22.6198991  28.6595816
## (Intercept) 237.8778663 265.4105287
## Days          7.1659594  13.2610425

Ejemplo: modelo gamma

En este ejemplo analizamos los datos de semiconductores tomados de Myers et al. (2002) sobre un experimento diseñado en una planta de semiconductores. Se emplean seis factores, temperatura de laminación, tiempo de laminación, presión de laminación, temperatura de cocción, tiempo de ciclo de cocción y punto de rocío de cocción, y estamos interesados en la curvatura de los dispositivos de sustrato producidos en la planta. La medición de la curvatura se realiza cuatro veces en cada dispositivo fabricado. Cada variable de diseño se toma en dos niveles. Se sabe que la medida no tiene una distribución normal y las medidas tomadas en el mismo dispositivo están correlacionadas.

Las variables de la base de datos se muestran a continuación.

• Device: Subtrate device
• x1: Lamination Temperature; two levels +1 and -1.
• x2: Lamination Time; two levels: +1 and -1.
• x3: Lamination Presure; two levels: +1 and -1.
• x4: Firing Temperature; two levels: +1 and -1.
• x5: Firing Cycle Time; two levels: +1 and -1.
• x6: Firing Dew Point: two levels: +1 and -1.
• y: Camber measure; in 1e-4 in./in.

El objetivo es ajustar el siguiente modelo a los datos.

\[\begin{align*} y_{ij} | b_0 &\sim Gamma(\mu_{ij}, \phi) \\ \log(\mu_{ij}) &= \beta_0 + \beta_1 x1_{ij} + \beta_3 x3_{ij} + \beta_5 x5_{ij} + \beta_6 x6_{ij} + b_{0i} \\ b_{0} &\sim N(0, \sigma^2_{b0}) \end{align*}\]

Solución.

Para ajustar el modelo anterior usamos el siguiente código.

library(hglm)
data(semiconductor)

library(glmmTMB)
fit <- glmmTMB(y ~ x1 + x3 + x5 + x6 + (1 | Device), 
               data = semiconductor,
               family = Gamma(link = log))

summary(fit)

##  Family: Gamma  ( log )
## Formula:          y ~ x1 + x3 + x5 + x6 + (1 | Device)
## Data: semiconductor
## 
##       AIC       BIC    logLik -2*log(L)  df.resid 
##    -545.2    -530.1     279.6    -559.2        57 
## 
## Random effects:
## 
## Conditional model:
##  Groups Name        Variance Std.Dev.
##  Device (Intercept) 0.02505  0.1583  
## Number of obs: 64, groups:  Device, 16
## 
## Dispersion estimate for Gamma family (sigma^2): 0.101 
## 
## Conditional model:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -4.69447    0.05635  -83.31  < 2e-16 ***
## x1           0.18290    0.05629    3.25 0.001158 ** 
## x3           0.30496    0.05629    5.42 6.04e-08 ***
## x5          -0.19565    0.05632   -3.47 0.000513 ***
## x6          -0.36961    0.05630   -6.57 5.19e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

De la tabla anterior podemos ver que el vector de parámetros con las siete estimaciones es:

\[ \hat{\boldsymbol{\Theta}} = (\hat{\beta_0}=-4.71, \hat{\beta_1}=0.18, \hat{\beta_3}=0.31, \hat{\beta_5}=-0.19, \hat{\beta_6}=-0.37, \hat{\phi}=0.101, \hat{\sigma}_{b0}=0.1583)^\top \]

Para obtener los intervalos de confianza usamos las siguientes instrucciones.

FUN <- function(model=fit) {
  temp_mod <- refit(fit, simulate(fit)[[1]])
  result <- c(as.numeric(temp_mod$fit$par[1:6]), # 1 a 6 para obtener
              temp_mod$obj$report()$sd[[1]])
  return(result)
}

b1 <- lme4::bootMer(fit, FUN, nsim=100, .progress="txt")

Para imprimir los intervalos de confianza de los 8 parámetros hacemos lo siguiente:

library(boot)

cat("95% Bootstrap confidence intervals for glmmTMB\n")

for (i in 1:7) {
  print(boot.ci(b1, type="perc", index=i)[4]$percent[4:5])
}

Luego del proceso de boostrap los intervalos de confianza obtenidos para cada estimación son:

## beta0 -4.805866 -4.563488
## beta1 0.07535473 0.27146044
## beta3 0.2029962 0.4109347
## beta5 -0.33692314 -0.07483849
## beta6 -0.4869687 -0.2227636
## phi 2.009481 2.775686
## sigma_b0 1.275266e-05 2.270661e-01

28.2 Intervalos de confianza para predicción

En esta sección se mostrará cómo utilizar el paquete ggeffects de Lüdecke (2025) para obtener intervalos de confianza para predicciones de un modelo lineal generalizado mixto.

Con el paquete ggeffects Sse pueden calcular predicciones ajustadas para muchos modelos diferentes. Los objetos de modelo compatibles actualmente son: averaging, bamlss, bayesglm, bayesx, betabin, betareg, bglmer, bigglm, biglm, blmer, bracl, brglm, brmsfit, brmultinom, cgam, cgamm, clm, clm2, clmm, coxph, feglm, fixest, flac, flic, gam, Gam, gamlss, gamm, gamm4, gee, geeglm, glimML, glm, glm.nb, glm_weightit, glmer.nb, glmerMod, glmgee, glmmPQL, glmmTMB, glmrob, glmRob, glmx, gls, hurdle, ivreg, lm, lm_robust, lme, lmerMod, lmrob, lmRob, logistf, logitr, lrm, mblogit, mclogit, MCMCglmm, merMod, merModLmerTest, MixMod, mixor, mlogit, multinom, multinom_weightit, negbin, nestedLogit, nlmerMod, ols, ordinal_weightit, orm, phyloglm, phylolm, plm, polr, rlm, rlmerMod, rq, rqs, rqss, sdmTMB, speedglm, speedlm, stanreg, survreg, svyglm, svyglm.nb, tidymodels, tobit, truncreg, vgam, vglm, wblm, wbm, Zelig-relogit, zeroinfl, zerotrunc.

A continuación se muestran dos ejemplos, un glmm normal de la clase lme4 y un glmm gamma de la clase glmmTMB.

Ejemplo: modelo normal

En este ejemplo vamos a retomar los datos sleepstudy del paquete lme4 de Bates et al. (2025) sobre el tiempo de reacción promedio por día para un conjunto de individuos en un estudio de privación del sueño. La base de datos contiene la información sobre el tiempo de reacción promedio (Reaction), el número de días de privación del sueño (Days), donde el día 0 corresponde al día en el que los individuos tenían su cantidad normal de sueño, y el número del individuo (en total 18) sobre el que se realizó la observación (Subject). A partir del día 0, hubo una restricción en cada individuo a 3 horas de sueño por noche.

Vamos a mostrar gráficamente los datos.

library(ggplot2)

ggplot(data = sleepstudy, aes(x = Days, y = Reaction, color = Subject)) +
  geom_point() +
  theme_bw() +
  facet_wrap(~ Subject) + labs(y = "Reaction time") + 
  theme(legend.position = "none")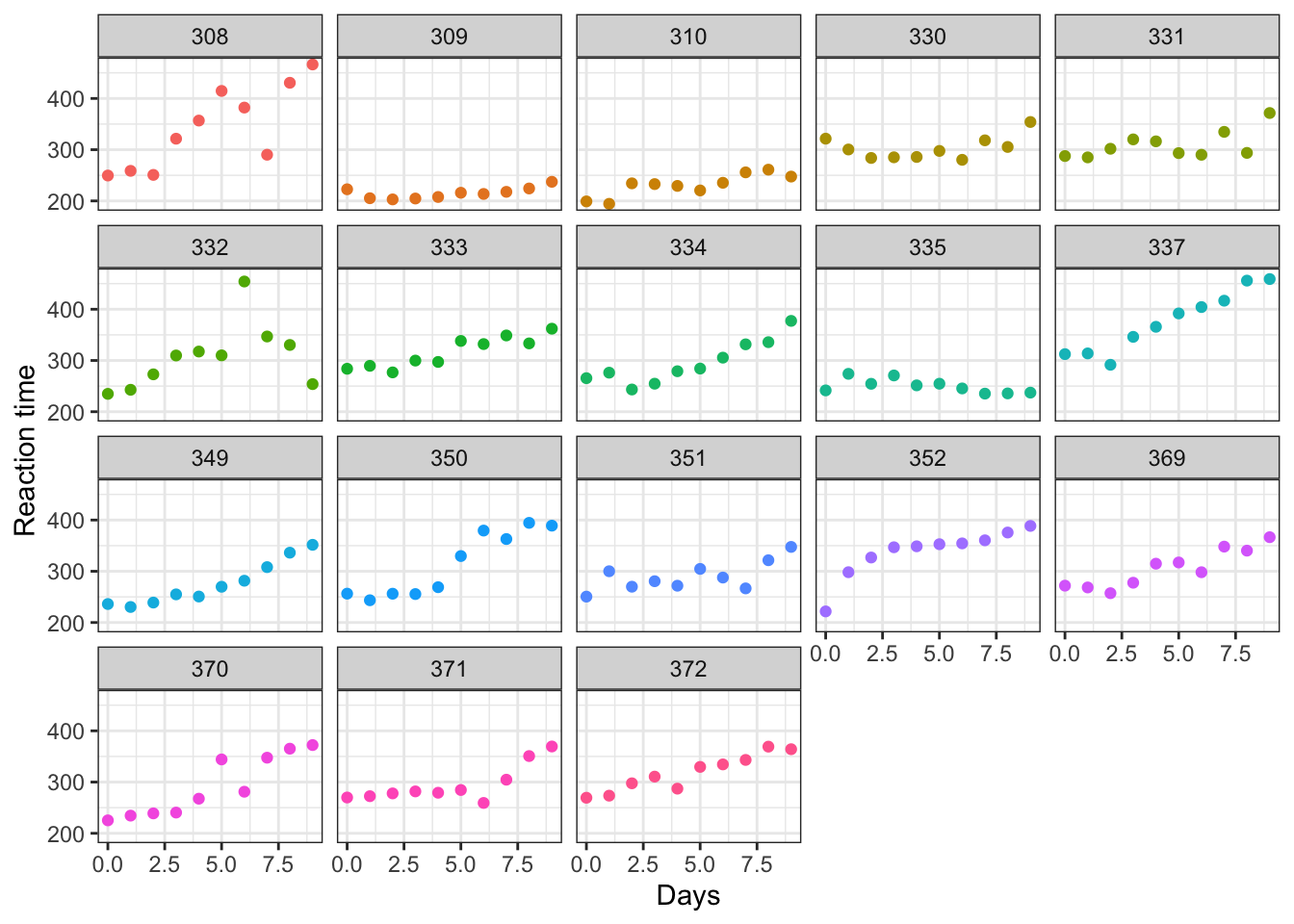

Ahora vamos a ajustar el modelo de interés.

library(ggeffects)
library(lme4)
data(sleepstudy)

fit <- lmer(Reaction ~ Days + (1 + Days | Subject), data = sleepstudy)

Para ver la tabla resumen con los resultados del modelo ajustado hacemos lo siguiente:

summary(fit)

## Linear mixed model fit by REML ['lmerMod']
## Formula: Reaction ~ Days + (1 + Days | Subject)
##    Data: sleepstudy
## 
## REML criterion at convergence: 1743.6
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.9536 -0.4634  0.0231  0.4634  5.1793 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr
##  Subject  (Intercept) 612.10   24.741       
##           Days         35.07    5.922   0.07
##  Residual             654.94   25.592       
## Number of obs: 180, groups:  Subject, 18
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)  251.405      6.825  36.838
## Days          10.467      1.546   6.771
## 
## Correlation of Fixed Effects:
##      (Intr)
## Days -0.138

Las predicciones de los interceptos y pendientes aleatorias (\(b_0\) y \(b_1\)) se pueden obtener con el código siguiente y son útiles para calcular \(\hat{\mu}\).

ranef(fit)

## $Subject
##     (Intercept)        Days
## 308   2.2585509   9.1989758
## 309 -40.3987381  -8.6196806
## 310 -38.9604090  -5.4488565
## 330  23.6906196  -4.8143503
## 331  22.2603126  -3.0699116
## 332   9.0395679  -0.2721770
## 333  16.8405086  -0.2236361
## 334  -7.2326151   1.0745816
## 335  -0.3336684 -10.7521652
## 337  34.8904868   8.6282652
## 349 -25.2102286   1.1734322
## 350 -13.0700342   6.6142178
## 351   4.5778642  -3.0152621
## 352  20.8636782   3.5360011
## 369   3.2754656   0.8722149
## 370 -25.6129993   4.8224850
## 371   0.8070461  -0.9881562
## 372  12.3145921   1.2840221
## 
## with conditional variances for "Subject"

Predicción para cada individuo

Ahora supongamos que nos interesa predecir el tiempo de reacción de los pacientes 335 y 337 en los días de observación 1, 5 y 9, y en los días 12, 15 que no fueron aún observados. Adicionalmente queremos los intervalos de confianza del 95% para la predicción en esos mismos días. Para eso vamos a usar la función predict_response() de la siguiente manera:

pre1 <- predict_response(model=fit,
                         ci_level=0.95, 
                         terms=c("Days [1, 5, 9, 12, 15]", 
                                 "Subject [335, 337]"), 
                         type="random")
pre1

## # Predicted values of Reaction
## 
## Subject: 335
## 
## Days | Predicted |         95% CI
## ---------------------------------
##    1 |    250.79 | 237.39, 264.18
##    5 |    249.65 | 230.74, 268.56
##    9 |    248.51 | 219.63, 277.38
##   12 |    247.65 | 210.42, 284.88
##   15 |    246.80 | 200.91, 292.69
## 
## Subject: 337
## 
## Days | Predicted |         95% CI
## ---------------------------------
##    1 |    305.39 | 292.00, 318.79
##    5 |    381.77 | 362.86, 400.68
##    9 |    458.16 | 429.28, 487.03
##   12 |    515.44 | 478.21, 552.67
##   15 |    572.73 | 526.84, 618.62

Como resultado se obtienen dos tablas, una para el paciente 335 y otra para el paciente 337. Cada tabla muestra los días, la predicción del tiempo de reacción promedio \(\mu\) y los intervalos de confianza del 95%. La predicción de \(\mu\) en este caso incluye los respectivos \(\tilde{b}_0\) y \(\tilde{b}_1\) obtenidos con ranef.

Es posible representar gráficamente la predicción y los intervalos usando la función genérica plot() sobre el objeto pre1 así:

plot(pre1, show_data = TRUE, show_ci = TRUE)

## Data points may overlap. Use the `jitter` argument to add some amount of
##   random variation to the location of data points and avoid overplotting.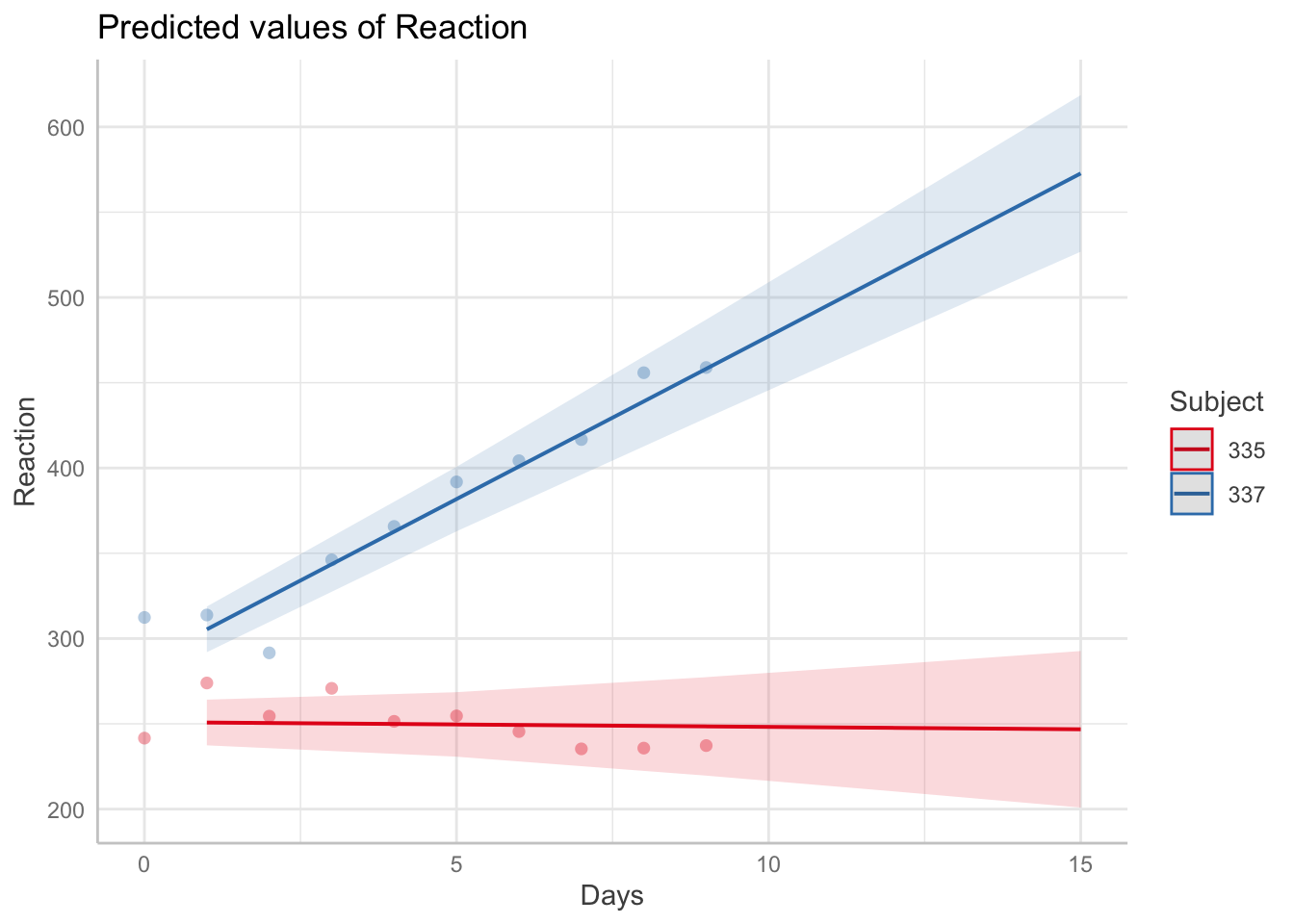

En la figura anterior se observan los modelos ajustados representados por las líneas continuas y los intervalos como sombras. Adicionalmente se observan unos puntos que corresponden a los datos originales para los pacientes considerados.

La figura anterior puede ser usada para monitorear la variable respuesta en los días 10, 11, 12 y siguientes. Los intervalos de confianza se hacen más anchos a medida que el número de días aumenta, esto es esperado ya que si queremos hacer una estimación lejos del día 9, muy seguramente tendremos más incertidumbre que para días cercanos al 9.

Predicciones condicionales

Las predicciones condicionales son predicciones para el parámetro \(\mu\) de la variable respuesta pensando en un paciente (o grupo) “típico”, es decir, predicciones para \(\mu\) sin incluir los efectos aleatorios predichos en la ecuación. Para obtener esta predicción se usa la función predict_response con margin="mean_reference".

Supongamos que nos interesa obtener predicciones condicionales con respecto a la variable días fijada en los valores de 1, 5, 9 y 12. El código para realizar esto es el siguiente:

# conditional predictions
pre2 <- predict_response(model=fit, 
                         terms="Days [1, 5, 9, 12]",
                         margin="mean_reference")
pre2

## # Predicted values of Reaction
## 
## Days | Predicted |         95% CI
## ---------------------------------
##    1 |    261.87 | 248.48, 275.27
##    5 |    303.74 | 284.83, 322.65
##    9 |    345.61 | 316.74, 374.48
##   12 |    377.01 | 339.78, 414.24
## 
## Adjusted for:
## * Subject = 0 (population-level)

Como resultado obtenemos una tabla con el valor predicho para \(\mu\) en los días solicitados y los intervalos de confianza.

Es posible representar estos resultados gráficamente de la siguiente manera.

plot(pre2, show_data = TRUE, show_ci = TRUE)

## Data points may overlap. Use the `jitter` argument to add some amount of
##   random variation to the location of data points and avoid overplotting.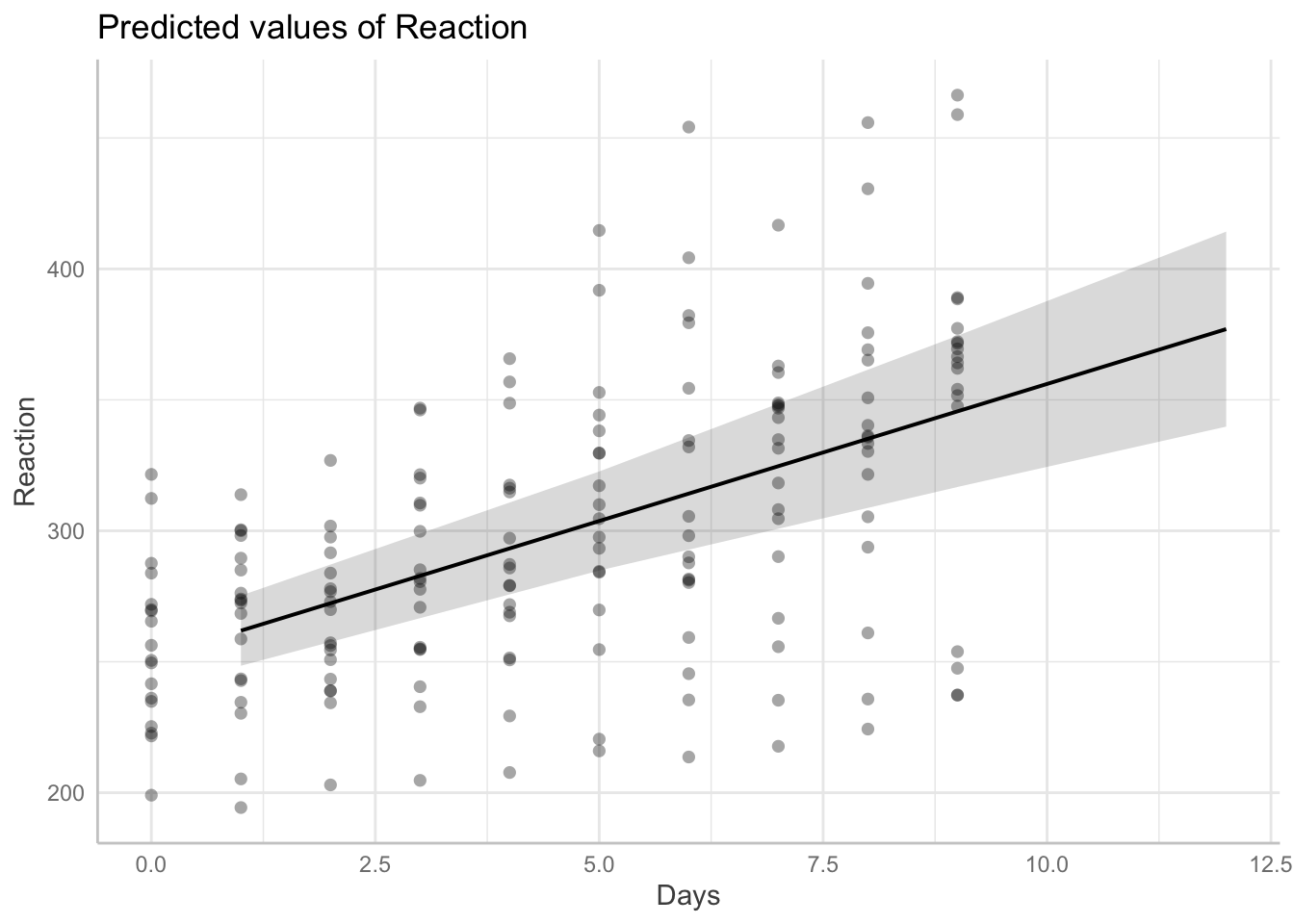

Predicciones marginales

Las predicciones marginales son predicciones para el parámetro \(\mu\) de la variable respuesta pensando en el efecto de una covariable \(X\) sobre todos los pacientes (o grupos) de forma general.

# average marginal predictions
pre3 <- predict_response(model=fit, 
                         terms="Days [1, 5, 9]", 
                         margin="empirical")
pre3

## # Average predicted values of Reaction
## 
## Days | Predicted |         95% CI
## ---------------------------------
##    1 |    261.87 | 248.48, 275.27
##    5 |    303.74 | 284.83, 322.65
##    9 |    345.61 | 316.74, 374.48

Como resultado obtenemos una tabla con el valor predicho para \(\mu\) en los días solicitados y los intervalos de confianza.

Es posible representar estos resultados gráficamente de la siguiente manera.

plot(pre3, show_data = TRUE, show_ci = TRUE)

## Data points may overlap. Use the `jitter` argument to add some amount of
##   random variation to the location of data points and avoid overplotting.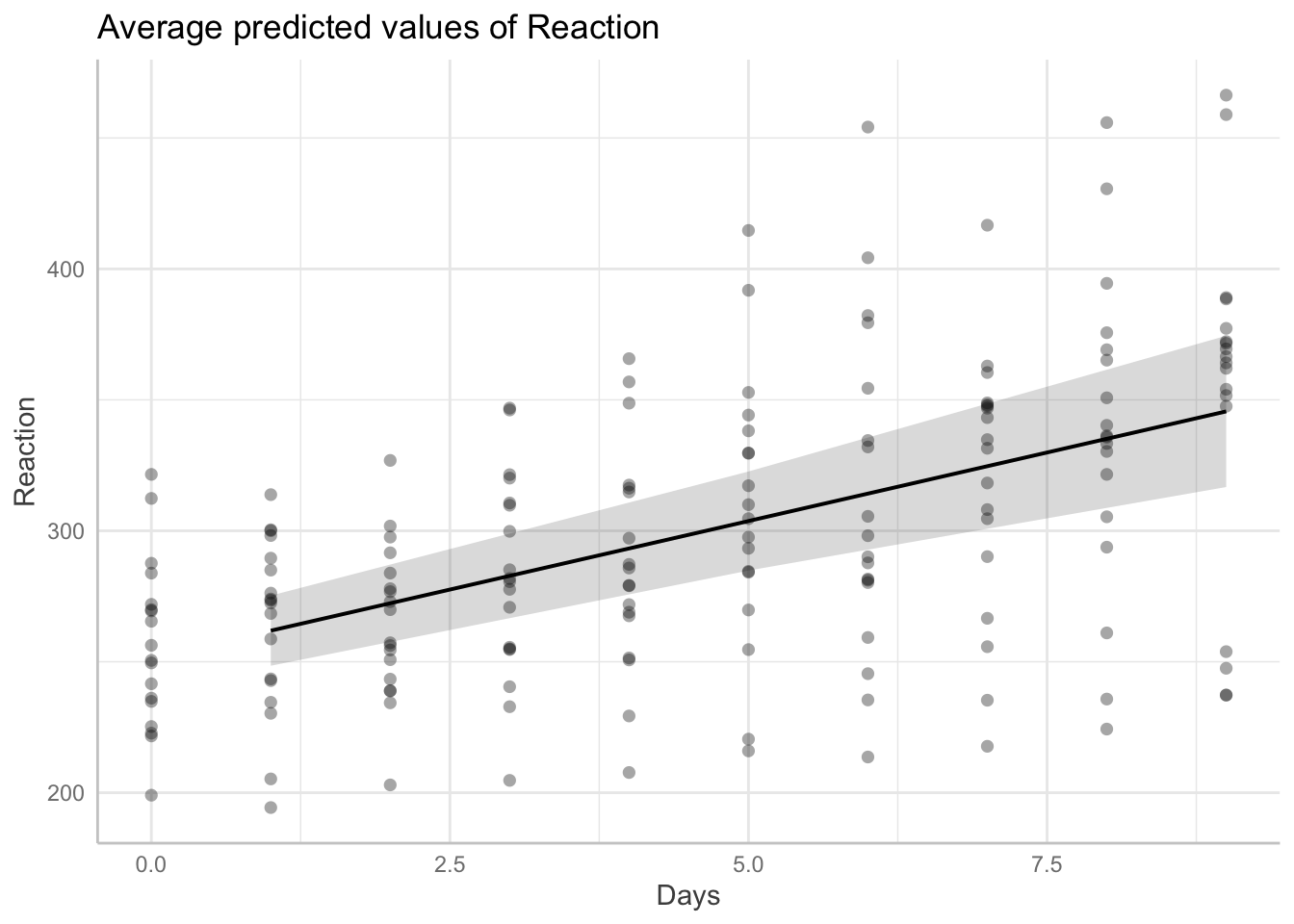

Cuando el conjunto de datos usados para ajustar el modelo tiene la misma cantidad de observaciones para cada grupo, las predicciones condicionales y marginales son muy similares. Pero cuando los grupos son desbalanceados, estas estimaciones difieren. Una explicación detallada de esta situación y un ejemplo puede consultarse en https://strengejacke.github.io/ggeffects/articles/introduction_randomeffects.html

Ejemplo: modelo gamma

En este ejemplo vamos a mostrar cómo obtener intervalos de confianza para un modelo con respuesta gamma. Para esto vamos a simular observaciones \(n_i=20\) observaciones para \(G=9\) grupos (en total 180 obs) que tengan la estructura mostrada abajo. El objetivo del ejemplo es mostrar cómo se obtienen los intervalos de confianza en varias situaciones.

\[\begin{align*} y_{ij} | b_0 &\sim Gamma(\mu_{ij}, \phi) \\ \log(\mu_{ij}) &= -2 + 3 x_{ij} + b_{0i} \\ \phi &= 0.5 \\ b_{0} &\sim N(0, \sigma^2_{b0}=2) \\ x &\sim U(0, 1) \end{align*}\]

Solución.

La función rgamma_glm que se muestra a continuación es una modificación de la función rgamma para tener la parametrización usada en los glm y que el parámetro \(\mu\) coincida con la media de la distribución.

rgamma_glm <- function(n, mu, phi) {
  x <- rgamma(n=n, shape=1/phi, scale=mu*phi)
  return(x)
}

A continuación el código para simular datos del modelo de interés.

ni <- 20
G <- 9
nobs <- ni * G
grupo <- factor(rep(x=1:G, each=ni))
obs <- rep(x=1:ni, times=G)
set.seed(123456)
x <- runif(n=nobs, min=0, max=1)
set.seed(123456)
b0 <- rnorm(n=G, mean=0, sd=sqrt(2)) # Intercepto aleatorio
b0 <- rep(x=b0, each=ni)             # El mismo intercepto aleatorio pero repetido
media <- exp(-2 + 3 * x + b0)
set.seed(123456)
y <- rgamma_glm(n=nobs, mu=media, phi=0.5)
datos <- data.frame(obs, grupo, b0, x, media, y)

En la siguiente figura se muestran los datos simulados para los nueve grupos considerados.

library(ggplot2)

ggplot(data = datos, aes(x = x, y = y, color = grupo)) +
  geom_point() +
  theme_bw() +
  facet_wrap(~ grupo) + labs(y = "Reaction time") + 
  theme(legend.position = "none")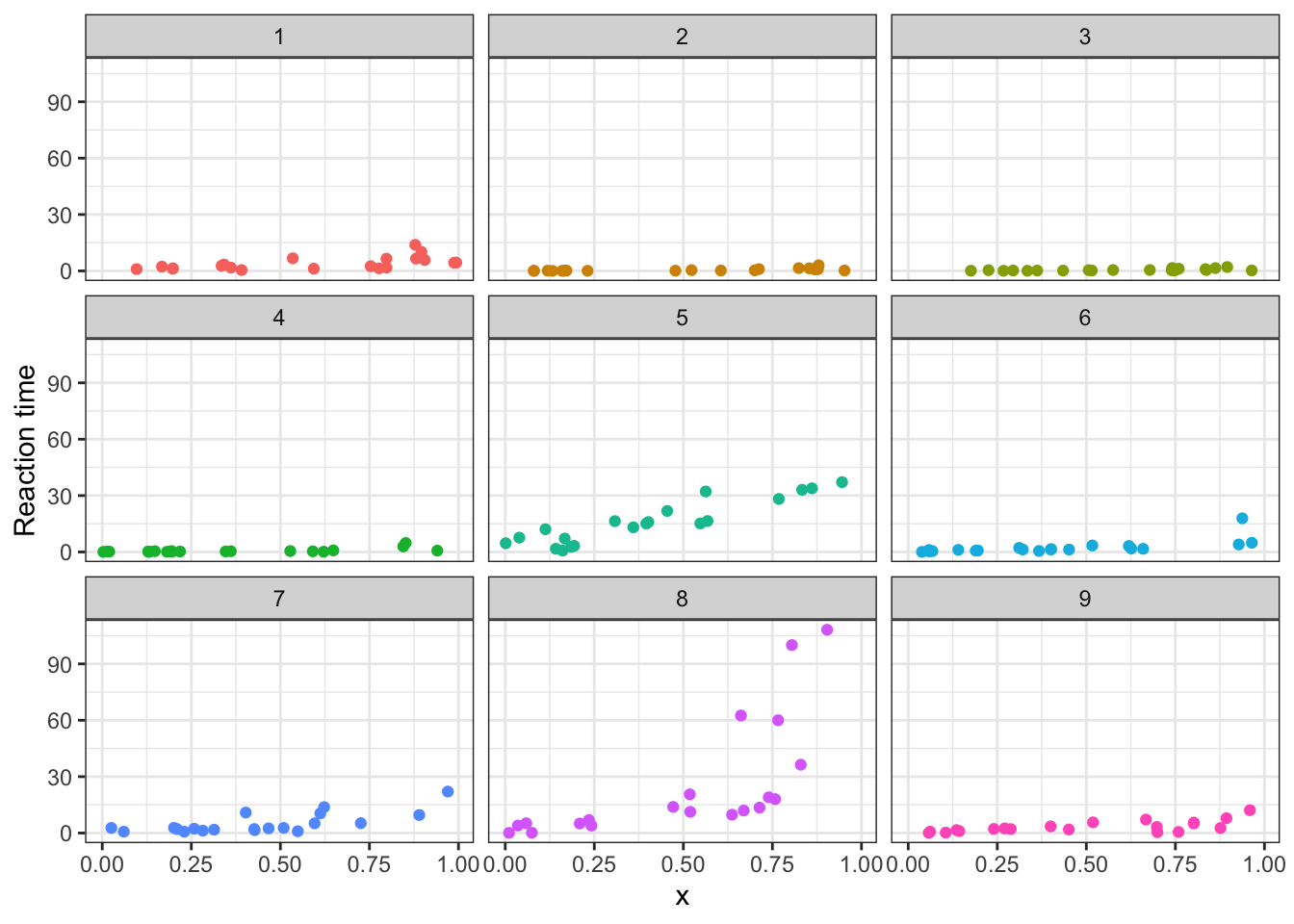

Ajustemos el modelo de interés usando la función glmmTMB del paquete glmmTMB de Brooks et al. (2025).

library(glmmTMB)
library(ggeffects)

fit <- glmmTMB(y ~ x + (1 | grupo), family=Gamma(link="log"), data=datos)

Para ver la tabla resumen con los resultados del modelo ajustado hacemos lo siguiente:

summary(fit)

##  Family: Gamma  ( log )
## Formula:          y ~ x + (1 | grupo)
## Data: datos
## 
##       AIC       BIC    logLik -2*log(L)  df.resid 
##     632.2     644.9    -312.1     624.2       176 
## 
## Random effects:
## 
## Conditional model:
##  Groups Name        Variance Std.Dev.
##  grupo  (Intercept) 1.93     1.389   
## Number of obs: 180, groups:  grupo, 9
## 
## Dispersion estimate for Gamma family (sigma^2): 0.511 
## 
## Conditional model:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -0.6840     0.4748  -1.441     0.15    
## x             2.9780     0.1887  15.781   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Las predicciones de los interceptos aleatorios \(b_0\) se pueden obtener con el código siguiente y son útiles para calcular \(\hat{\mu}\).

ranef(fit)

## $grupo
##   (Intercept)
## 1  0.19343037
## 2 -1.94246345
## 3 -1.84730623
## 4 -1.28076294
## 5  2.01846111
## 6 -0.08977021
## 7  0.73895864
## 8  1.90427682
## 9  0.19304021

Predicción para cada individuo

Supongamos que nos interesa predecir la media de la variable respuesta \(Y\) del grupo 2 y 4 en los valores \(X\) de 0.2, 0.6 y 0.8, y en los valores 1.2, 1.5 que no fueron aún observados. Adicionalmente queremos los intervalos de confianza del 95% para la predicción en esos mismos valores de \(X\). Para eso vamos a usar la función predict_response() de la siguiente manera:

pre1 <- predict_response(fit, 
                         ci_level=0.95, 
                         terms=c("x [0.2, 0.6, 0.8, 1.2, 1.5]",
                                 "grupo [2, 4]"),
                         type="random"
                         )
pre1

## # Predicted values of y
## 
## grupo: 2
## 
##    x | Predicted |      95% CI
## ------------------------------
## 0.20 |      0.13 | 0.09,  0.19
## 0.60 |      0.43 | 0.31,  0.59
## 0.80 |      0.78 | 0.57,  1.08
## 1.20 |      2.58 | 1.75,  3.80
## 1.50 |      6.30 | 3.98,  9.98
## 
## grupo: 4
## 
##    x | Predicted |      95% CI
## ------------------------------
## 0.20 |      0.25 | 0.18,  0.35
## 0.60 |      0.84 | 0.60,  1.16
## 0.80 |      1.52 | 1.07,  2.16
## 1.20 |      5.00 | 3.22,  7.75
## 1.50 |     12.21 | 7.24, 20.59

Como resultado se obtienen dos tablas, una para el grupo 2 y otra para el grupo 4. Cada tabla muestra los valores de \(X\), la predicción de \(\mu\) y los intervalos de confianza del 95%. La predicción de \(\mu\) en este caso incluye los respectivos \(\tilde{b}_0\) obtenidos con ranef.

Es posible representar gráficamente la predicción y los intervalos usando la función genérica plot() sobre el objeto pre1 así:

plot(pre1, show_data = TRUE, show_ci = TRUE)

## Data points may overlap. Use the `jitter` argument to add some amount of
##   random variation to the location of data points and avoid overplotting.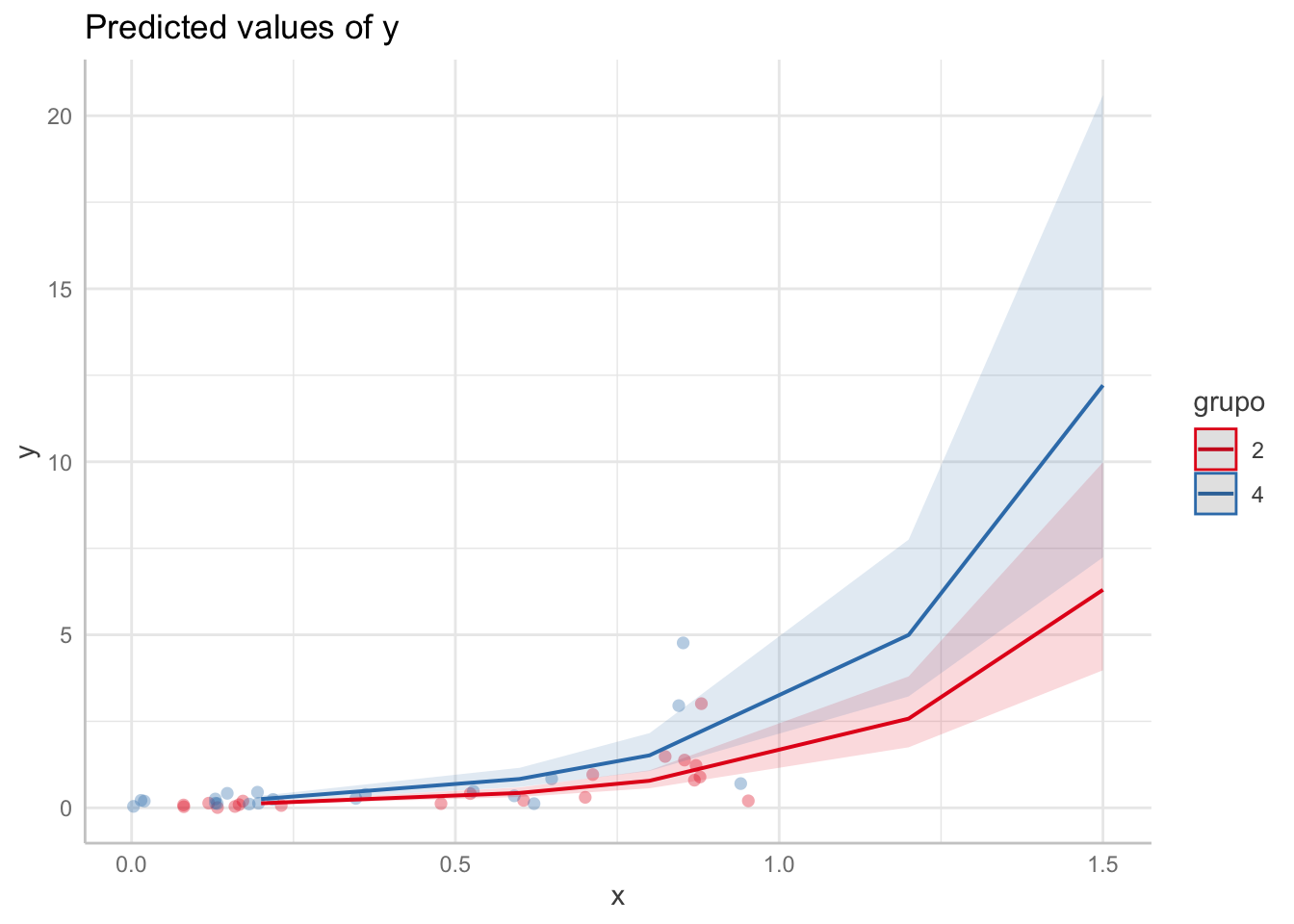

En la figura anterior se observan los modelos ajustados representados por las líneas continuas y los intervalos como sombras. Adicionalmente se observan unos puntos que corresponden a los datos originales para los grupos considerados.

La figura anterior puede ser usada para monitorear la variable respuesta en los valores \(X\) de 0.2, 0.4, 0.6 y siguientes. Los intervalos de confianza se hacen más anchos a medida que \(X\) aumenta, esto es esperado ya que si queremos hacer una estimación lejos de \(X=1\), muy seguramente tendremos más incertidumbre que para valores cercanos a 1.

Predicciones condicionales

Las predicciones condicionales son predicciones para el parámetro \(\mu\) de la variable respuesta pensando en un grupo “típico”, es decir, predicciones para \(\mu\) sin incluir los efectos aleatorios predichos en la ecuación. Para obtener esta predicción se usa la función predict_response con margin="mean_reference".

Supongamos que nos interesa obtener predicciones condicionales con respecto a la variable \(X\) fijada en los valores de 0.2, 0.4 y 0.6. El código para realizar esto es el siguiente:

# conditional predictions
pre2 <- predict_response(model=fit, 
                         terms="x [0.2, 0.4, 0.6]",
                         margin="mean_reference")

## You are calculating adjusted predictions on the population-level (i.e.
##   `type = "fixed"`) for a *generalized* linear mixed model.
##   This may produce biased estimates due to Jensen's inequality. Consider
##   setting `bias_correction = TRUE` to correct for this bias.
##   See also the documentation of the `bias_correction` argument.

pre2

## # Predicted values of y
## 
##    x | Predicted |     95% CI
## -----------------------------
## 0.20 |      0.92 | 0.36, 2.30
## 0.40 |      1.66 | 0.67, 4.14
## 0.60 |      3.01 | 1.21, 7.52
## 
## Adjusted for:
## * grupo = NA (population-level)

Como resultado obtenemos una tabla con el valor predicho para \(\mu\) en los días solicitados y los intervalos de confianza.

Es posible representar estos resultados gráficamente de la siguiente manera.

plot(pre2, show_data = TRUE, show_ci = TRUE)

## Data points may overlap. Use the `jitter` argument to add some amount of
##   random variation to the location of data points and avoid overplotting.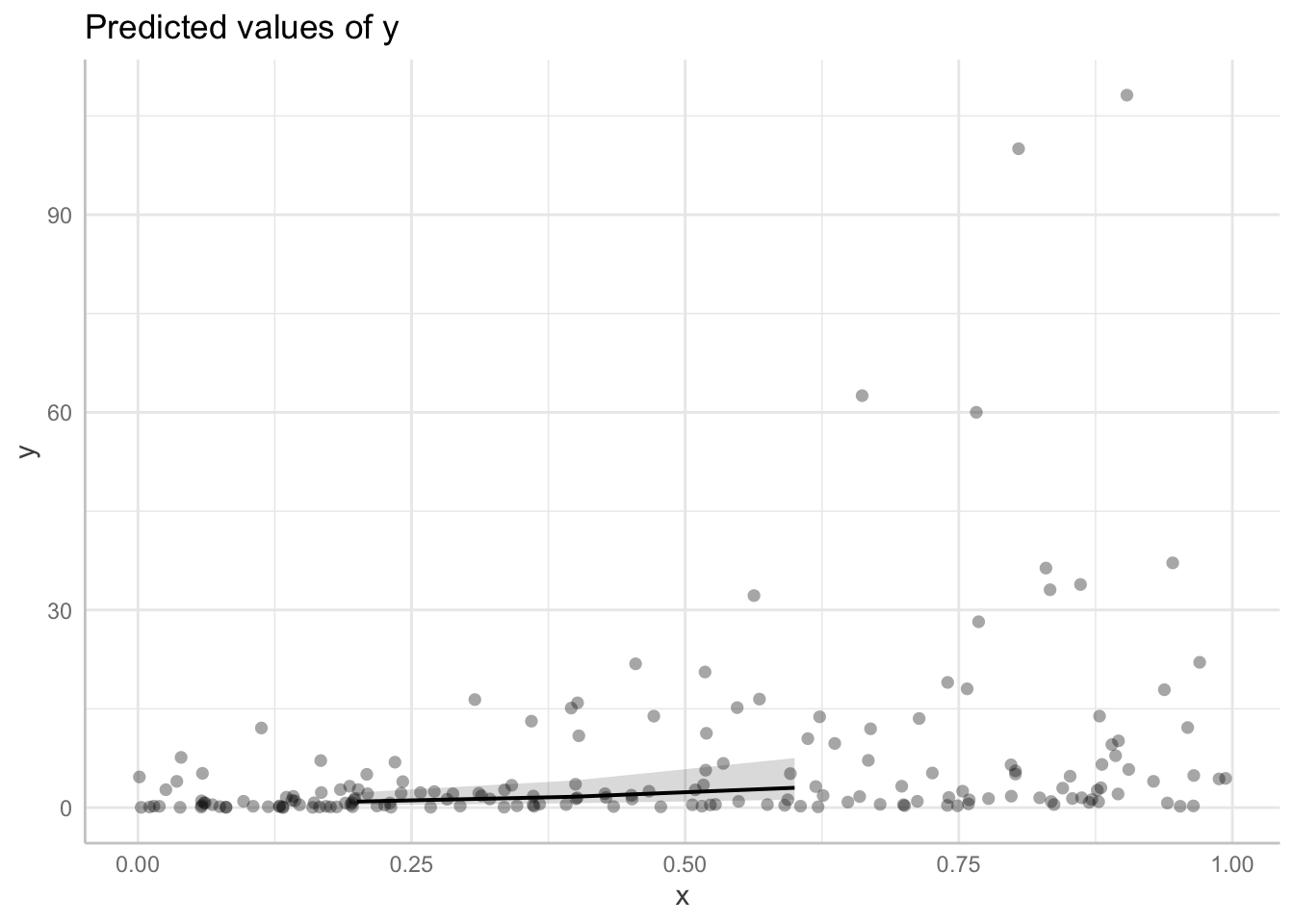

Predicciones marginales

Las predicciones marginales son predicciones para el parámetro \(\mu\) de la variable respuesta pensando en el efecto de una covariable \(X\) sobre todos los grupos de forma general.

# average marginal predictions
pre3 <- predict_response(model=fit, 
                         terms="x [0.2, 0.4, 0.6]", 
                         margin="empirical")
pre3

## # Average predicted values of y
## 
##    x | Predicted |      95% CI
## ------------------------------
## 0.20 |      2.06 | 0.17,  3.95
## 0.40 |      3.74 | 0.32,  7.15
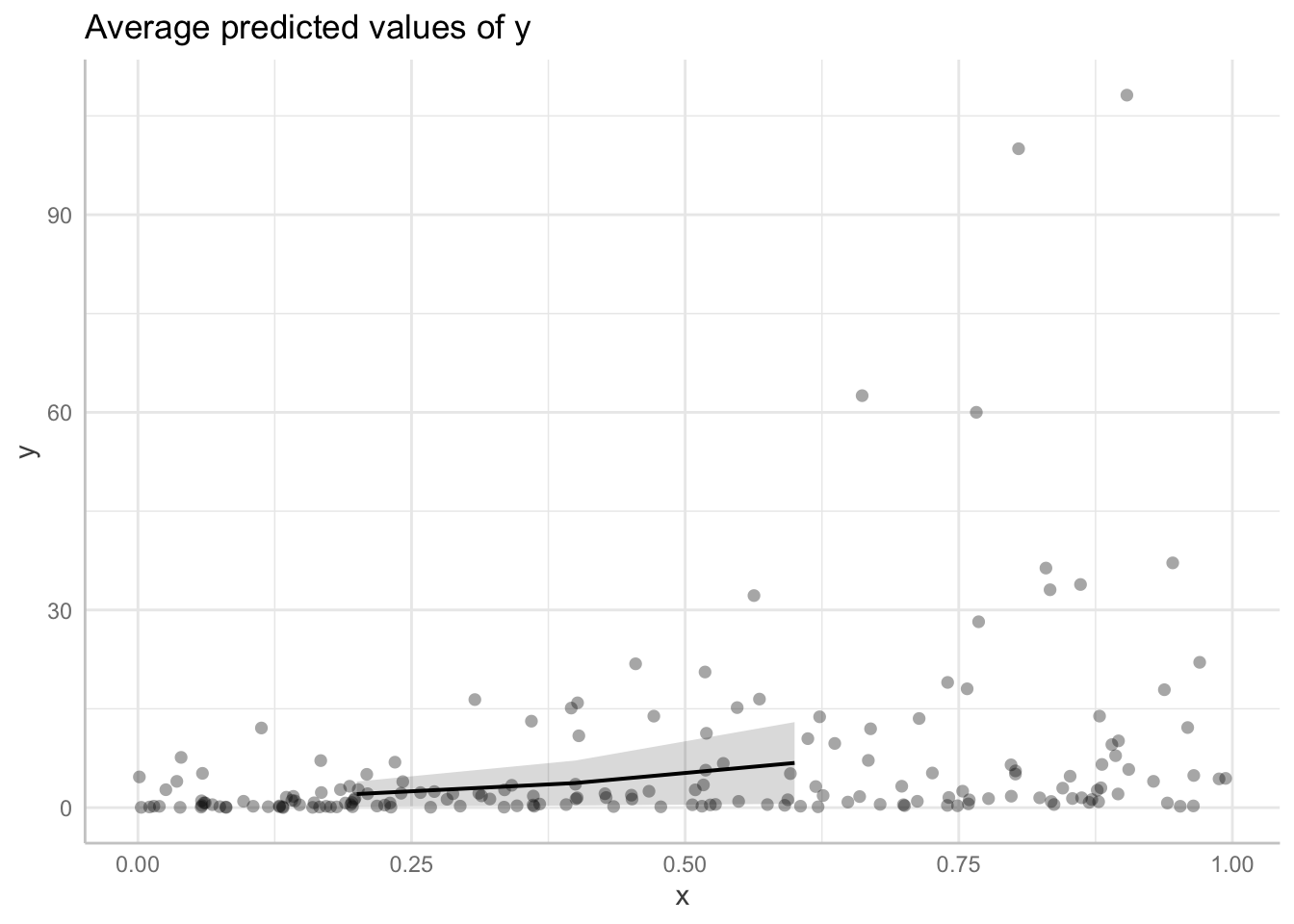
## 0.60 |      6.78 | 0.58, 12.98

Como resultado obtenemos una tabla con el valor predicho para \(\mu\) en los días solicitados y los intervalos de confianza.

Es posible representar estos resultados gráficamente de la siguiente manera.

plot(pre3, show_data = TRUE, show_ci = TRUE)

## Data points may overlap. Use the `jitter` argument to add some amount of
##   random variation to the location of data points and avoid overplotting.

Para comprender las diferencias entre estimación marginal y estimación condicional se recomienda consultar esta publicación donde se explican en detalle las diferencias.

References

Bates, Douglas, Martin Maechler, Ben Bolker, and Steven Walker. 2025. Lme4: Linear Mixed-Effects Models Using Eigen and S4. https://github.com/lme4/lme4/.

Brooks, Mollie, Ben Bolker, Kasper Kristensen, Martin Maechler, Arni Magnusson, Hans Skaug, Anders Nielsen, Casper Berg, and Koen van Bentham. 2025. glmmTMB: Generalized Linear Mixed Models Using Template Model Builder. https://github.com/glmmTMB/glmmTMB.

Lüdecke, Daniel. 2025. Ggeffects: Create Tidy Data Frames of Marginal Effects for Ggplot from Model Outputs. https://strengejacke.github.io/ggeffects/.