19 Paquete glmm
El paquete glmm de Knudson (2024) aproxima la verosimilitud de un modelo mixto lineal generalizado mediante aproximación de Monte Carlo. Al visitar este enlace se encontrará la página de apoyo del paquete, allí se puede consultar el manual de referencia y las viñetas.
19.1 Función glmm
La función glmm es la principal función del paquete glmm. Esta función sirve para ajustar un glmm y su estructura es la siguiente:
glmm(fixed, random, varcomps.names, data, family.glmm, m,
varcomps.equal, weights=NULL, doPQL = TRUE,debug=FALSE,
p1=1/3,p2=1/3, p3=1/3, rmax=1000,iterlim=1000, par.init, zeta=5, cluster=NULL)Los principales argumentos de la función son:
formula: es una fórmula similar a la usada en el modelo lineal clásico. Un ejemplo de fórmula seríay ~ 1 + x1 + x2.random: es una fórmula solo con lado derecho. Si queremos indicar intercepto aleatorio se escribe~ 1 | groupy si se desea intercepto y pendiente aleatoria se escribe~ 1 + x2 | group.data: marco de datos donde están las variables.family.glm: argumento para indicar la distribución de la variable respuesta.
Ejemplo: modelo Poisson con intercepto aleatorio
En este ejemplo vamos a simular \(n_i=50\) observaciones para \(G=10\) grupos (en total 500 obs) que tengan la estructura mostrada abajo. El objetivo del ejemplo es ilustrar el uso de la función glmm para estimar los parámetros del modelo.
\[\begin{align*} y_{ij} | b_0 &\sim Poisson(\mu_{ij}) \\ \log(\mu_{ij}) &= 4 - 6 x_{ij} + b_{0i} \\ b_{0} &\sim N(0, \sigma^2_{b0}=4) \\ x_{ij} &\sim U(0, 1) \end{align*}\]
El vector de parámetros de este modelo es \(\boldsymbol{\Theta}=(\beta_0=4, \beta_1=-6, \sigma^2_{b0}=4)^\top\).
El código para simular las observaciones se muestra a continuación.
ni <- 50
G <- 10
nobs <- ni * G
grupo <- factor(rep(x=1:G, each=ni))
obs <- rep(x=1:ni, times=G)
x <- runif(n=nobs, min=0, max=1)
b0 <- rnorm(n=G, mean=0, sd=sqrt(4)) # Intercepto aleatorio
b0 <- rep(x=b0, each=ni) # El mismo intercepto aleatorio pero repetido
media <- exp(4 - 6 * x + b0)
y <- rpois(n=nobs, lambda=media)
datos <- data.frame(obs, grupo, b0, x, y)Vamos a explorar los datos simulados.
El siguiente paso es dibujar los datos para explorar si sería apropiado usar un modelo con intercepto aleatorio (obvio porque así se simularon los datos). El código para dibujar los datos se muestra abajo.
library(ggplot2)
ggplot(datos, aes(x, y, color=grupo) ) +
geom_point() +
labs(colour="Grupo/Cluster")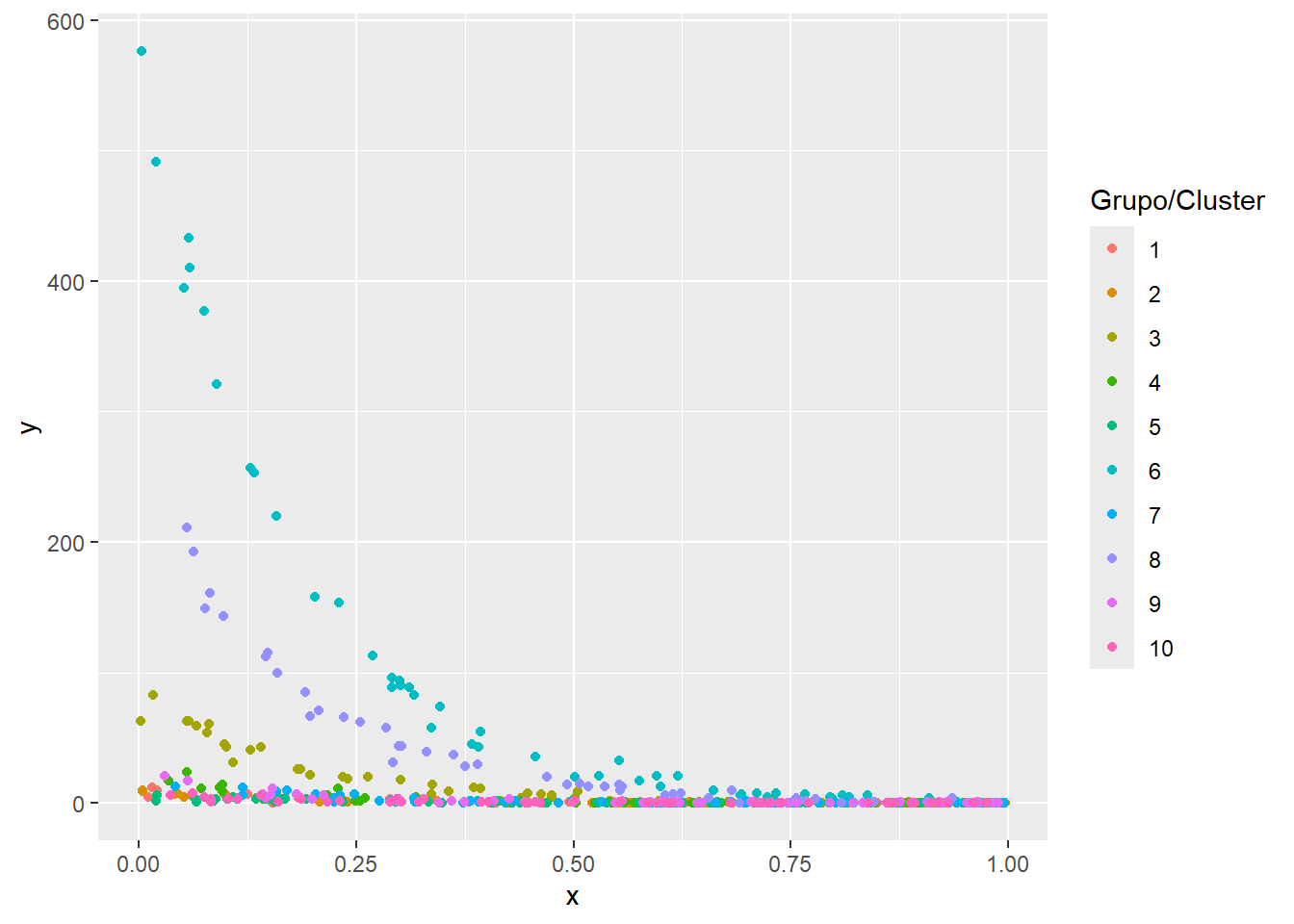
Para estimar los parámetros del modelo se usa la función glmm de la siguiente forma. Vamos a usar m=10 para que no se demore, usted puede repetir el ejemplo aumentando m.
library(glmm)
fit1 <- glmm(y ~ x, random = list(y ~ 0 + grupo), varcomps.names = c("b0"),
family.glmm = poisson.glmm, data = datos, m = 10)Existen varias funciones genéricas que se pueden utilizar para recuperar el vector de parámetros \(\boldsymbol{\Theta}=(\beta_0=4, \beta_1=-6, \sigma^2_{b0}=4)^\top\). Abajo el código para realizarlo.
## (Intercept) x
## 3.358885 -6.086647## b0
## 2.278676## [1] 32994.65También se pueden extraer los valores del objeto fit1 así.
## (Intercept) x
## 3.358885 -6.086647## b0
## 2.278676## [1] 32994.65De la salida anterior vemos que el vector de parámetros estimados es \(\hat{\boldsymbol{\Theta}}=(3.3588854, -6.0866473, 2.2786759)^\top\) mientras que el verdadero es \(\boldsymbol{\Theta}=(\beta_0=4, \beta_1=-6, \sigma^2_{b0}=4)^\top\).