18 Paquete glmmTMB
El paquete glmmTMB de Brooks et al. (2025) se utiliza para estimar modelos glmm por medio de máxima verosimilitud a través de ‘TMB’ (Template Model Builder). Se supone que los efectos aleatorios son gaussianos en la escala del predictor lineal y se integran utilizando la aproximación de Laplace. Los gradientes se calculan mediante la diferenciación automática. Al visitar este enlace se encontrará la página de apoyo del paquete, allí se puede consultar el manual de referencia y las viñetas.
18.1 Función glmmTMB
La función glmmTMB es la principal función del paquete glmmTMB. Esta función sirve para ajustar un glmm y su estructura es la siguiente:
glmmTMB(formula,
data = NULL,
family = gaussian(),
ziformula = ~0,
dispformula = ~1,
weights = NULL,
offset = NULL,
contrasts = NULL,
na.action,
se = TRUE,
verbose = FALSE,
doFit = TRUE,
control = glmmTMBControl(),
REML = FALSE,
start = NULL,
map = NULL,
sparseX = NULL
)Los principales argumentos de la función son:
formula: es una fórmula similar a la usada en el modelo lineal clásico. Un ejemplo de fórmula seríay ~ 1 + x1 + x2 + (1 + x2 | grupo)con la cual se indican los efectos fijos y los efectos aleatorios del modelo. Más abajo hay una tabla con más detalles sobre la fórmula.data: marco de datos donde están las variables.family: argumento para indicar la distribución de la variable respuesta.REML: valor lógico que sirve para indicar si queremos estimaciones maximizando la verosimilitud restringida o la verosimilitud usual.
Ejemplo: modelo normal con intercepto aleatorio
En este ejemplo vamos a simular observaciones \(n_i=50\) observaciones para \(G=10\) grupos (en total 500 obs) que tengan la estructura mostrada abajo. El objetivo del ejemplo es ilustrar el uso de la función glmmTMB para estimar los parámetros del modelo.
\[\begin{align*} y_{ij} | b_0 &\sim N(\mu_{ij}, \sigma^2_y) \\ \mu_{ij} &= 4 - 6 x_{ij} + b_{0i} \\ \sigma^2_y &= 16 \\ b_{0} &\sim N(0, \sigma^2_{b0}=625) \\ x_{ij} &\sim U(-5, 6) \end{align*}\]
El vector de parámetros de este modelo es \(\boldsymbol{\Theta}=(\beta_0=4, \beta_1=-6, \sigma_y=4, \sigma_{b0}=25)^\top\).
El código para simular las 500 observaciones se muestra a continuación. Observe que se fijó la semilla en dos ocasiones para que el lector pueda replicar el ejemplo y obtener los mismos resultados.
ni <- 50
G <- 10
nobs <- ni * G
grupo <- factor(rep(x=1:G, each=ni))
obs <- rep(x=1:ni, times=G)
set.seed(1234567)
x <- runif(n=nobs, min=-5, max=6)
set.seed(1234567)
b0 <- rnorm(n=G, mean=0, sd=sqrt(625)) # Intercepto aleatorio
b0 <- rep(x=b0, each=ni) # El mismo intercepto aleatorio pero repetido
media <- 4 - 6 * x + b0
set.seed(1234567)
y <- rnorm(n=nobs, mean=media, sd=sqrt(16))
datos <- data.frame(obs, grupo, b0, x, media, y)Vamos a explorar los datos simulados.
El siguiente paso es dibujar los datos para explorar si sería apropiado usar un modelo con intercepto aleatorio (obvio porque así se simularon los datos). El código para dibujar los datos se muestra abajo.
library(ggplot2)
ggplot(datos, aes(x, y, color=grupo) ) +
geom_point() +
labs(colour="Grupo/Cluster")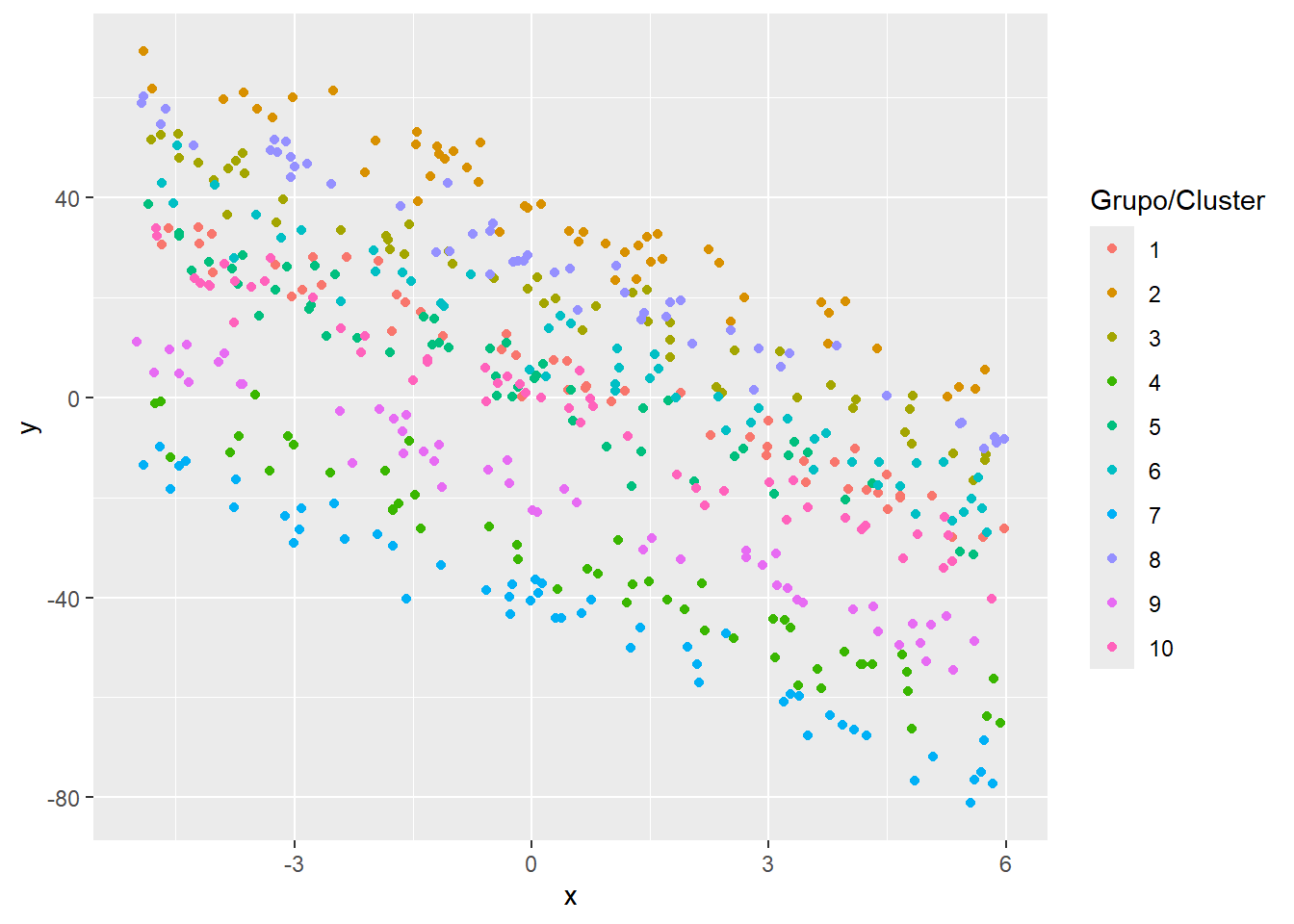
En la figura anterior se observa un patrón claro, todas las 10 nubes de puntos tienen la misma pendiente pero diferente intercepto con el eje vertical, eso se debe a que en la simulación se incluyó un \(b_0\).
Para estimar los parámetros del modelo se usa la función glmmTMB de la siguiente forma.
La función summary se puede usar sobre el objeto fit1 para obtener una tabla de resumen, a continuación se ilustra el uso y la salida de summary.
## Family: gaussian ( identity )
## Formula: y ~ x + (1 | grupo)
## Data: datos
##
## AIC BIC logLik -2*log(L) df.resid
## 2871.3 2888.1 -1431.6 2863.3 496
##
## Random effects:
##
## Conditional model:
## Groups Name Variance Std.Dev.
## grupo (Intercept) 579.20 24.066
## Residual 15.46 3.931
## Number of obs: 500, groups: grupo, 10
##
## Dispersion estimate for gaussian family (sigma^2): 15.5
##
## Conditional model:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.23780 7.61256 0.29 0.769
## x -6.02640 0.05614 -107.35 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Según el resultado anterior \(\hat{\boldsymbol{\Theta}}=(\hat{\beta}_0=2.2378, \hat{\beta}_1=-6.0264, \hat{\sigma}_y=3.931, \hat{\sigma}_{b0}=24.066)^\top\) mientras que el vector real de parámetros es \(\boldsymbol{\Theta}=(\beta_0=4, \beta_1=-6, \sigma_y=4, \sigma_{b0}=25)^\top\).
Compare los resultados de la tabla anterior obtenida con la función lmer anterior con los resultados obtenidos con la función lme de capítulo 7.
Ejemplo: recuperando los interceptos aleatorios
¿Cómo se pueden obtener los interceptos aleatorios a partir del modelo ajustado en la sección anterior?
Para obtener los interceptos aleatorios se usa la función ranef del paquete glmmTMB de Brooks et al. (2025). A continuación vamos a obtener los interceptos aleatorios y los vamos a comparar con los \(b_0\) simulados.
## b0
## [1,] 3.917594
## [2,] 34.345280
## [3,] 18.266756
## [4,] -33.770023
## [5,] -0.212874
## [6,] 8.024547
## [7,] -44.453710
## [8,] 22.737596
## [9,] -22.985108
## [10,] -3.942871De la salida anterior vemos que los \(\tilde{b}_0\) son cercanos a los valores reales de \(b_0\).
Ejemplo: modelo gamma con intercepto aleatorio
En este ejemplo vamos a simular observaciones \(n_i=20\) observaciones para \(G=10\) grupos (en total 200 obs) que tengan la estructura mostrada abajo. El objetivo del ejemplo es ilustrar el uso de la función glmmTMB para estimar los parámetros del modelo.
\[\begin{align*} y_{ij} | b_0 &\sim Gamma(\mu_{ij}, \phi) \\ \log(\mu_{ij}) &= 2 - 8 x_{ij} + b_{0i} \\ \phi &= 0.5 \\ b_{0} &\sim N(0, \sigma^2_{b0}=9) \\ x &\sim U(0, 1) \end{align*}\]
El vector de parámetros de este modelo es \(\boldsymbol{\Theta}=(\beta_0=2, \beta_1=-8, \phi=0.5, \sigma_{b0}=3)^\top\).
La función rgamma_glm que se muestra a continuación es una modificación de la función rgamma para tener la parametrización usada en los glm y que el parámetro \(\mu\) coincida con la media de la distribución.
A continuación el código para simular datos del modelo de interés.
ni <- 20
G <- 10
nobs <- ni * G
grupo <- factor(rep(x=1:G, each=ni))
obs <- rep(x=1:ni, times=G)
set.seed(123456)
x <- runif(n=nobs, min=0, max=1)
set.seed(123456)
b0 <- rnorm(n=G, mean=0, sd=sqrt(9)) # Intercepto aleatorio
b0 <- rep(x=b0, each=ni) # El mismo intercepto aleatorio pero repetido
media <- exp(2 - 8 * x + b0)
set.seed(123456)
y <- rgamma_glm(n=nobs, mu=media, phi=0.5)
datos <- data.frame(obs, grupo, b0, x, media, y)Vamos a explorar los datos simulados.
El siguiente paso es explorar los datos simulados. El código para dibujar los datos se muestra abajo.
library(ggplot2)
ggplot(datos, aes(x, y, color=grupo) ) +
geom_point() +
labs(colour="Grupo/Cluster")
Para estimar los parámetros del modelo se usa la función glmmTMB de la siguiente forma.
La función summary se puede usar sobre el objeto fit2 para obtener una tabla de resumen, a continuación se la salida de summary.
## Family: Gamma ( log )
## Formula: y ~ x + (1 | grupo)
## Data: datos
##
## AIC BIC logLik -2*log(L) df.resid
## 595.9 609.1 -294.0 587.9 196
##
## Random effects:
##
## Conditional model:
## Groups Name Variance Std.Dev.
## grupo (Intercept) 9.073 3.012
## Number of obs: 200, groups: grupo, 10
##
## Dispersion estimate for Gamma family (sigma^2): 0.507
##
## Conditional model:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 4.4102 0.9581 4.60 4.16e-06 ***
## x -8.0789 0.1830 -44.14 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Según el resultado anterior \(\hat{\boldsymbol{\Theta}}=(\hat{\beta}_0=4.4102, \hat{\beta}_1=-8.0789, \hat{\phi}=0.507, \hat{\sigma}_{bo}=3.012)^\top\) mientras que el vector real de parámetros es \(\boldsymbol{\Theta}=(\beta_0=2, \beta_1=-8, \phi=0.50, \sigma_{b0}=3)^\top\).