5 Support Vector Machines para regresión
Drucker et al. (1997) en el artículo titulado “Support Vector Regression Machines” propusieron las máquinas de soporte vectorial (svm) para el problema de regresión.
En la siguiente figura (tomada de link) se ilustra la idea intuitiva para el caso de predecir \(y\) usando una sola variable \(x\).
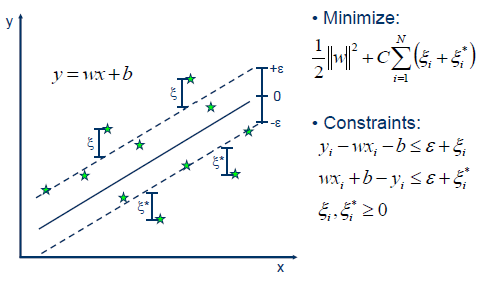
El objetivo es construir un margen de tolerancia (\(\varepsilon\)) con el cual se tendrán observaciones dentro de los márgenes y fuera de los márgenes. Usando sólo las observaciones fuera de los márgenes, se calculan los errores \(\xi\) o \(\xi^\star\) y con ellos se construye la función de objetivo (FO) a minimizar
\[ \text{FO} = \frac{1}{2} \| \boldsymbol{w} \|^2 + C \sum_{i=1}^{m} (\xi_i + \xi^\star_i), \]
donde \(\boldsymbol{w}\) es el vector con las pendientes asociadas a cada una de las variables (sin incluir intercepto), \(C\) es un valor de penalización para los errores y \(m\) el número de observaciones que están fuera de los márgenes del total de \(n\) observaciones.
Paquetes de R para svm
Los paquetes más conocidos para svm son:
Existen otros paquetes que el lector puede consultar en la sección Support Vector Machines and Kernel Methods CRAN Task View: Machine Learning & Statistical Learning.
Ventajas
Algunas de las ventajas de SVM según Shivaswamy, Chu, and Jansche (2007) son:
- superior generalization capacity,
- globally optimal solution from a convex optimization problem,
- ability to handle non-linear problems using the so-called “kernel trick”,
- sparseness of the solution which makes it possible to have specialized fast algorithms such as the sequential minimal optimization.