9 Regresión lineal versus árboles de regresión

En este capítulo se muestra una comparación entre modelos de regresión y árboles de regresion.

Regresión lineal

El modelo de regresión lineal simple es uno de los más populares en modelación. Este modelo se puede resumir a continuación.

\[\begin{align} y_i &\sim N(\mu_i, \sigma^2), \\ \mu_i &= \beta_0 + \beta_1 x_i, \\ \sigma^2 &= \text{constante} \end{align}\]

Arboles de regresión

Una explicación de los árboles de regresión puede ser consultada en el capítulo 1.

Las librerías en R para implementar árboles de regresión son:

library(rpart)
library(rpart.plot)

Ejemplo

Como ilustración vamos a usar los datos del ejemplo 2.1 del libro de Montgomery, Peck and Vining (2003). En el ejemplo 2.1 los autores ajustaron un modelo de regresión lineal simple para explicar la Resistencia de una soldadura en función de la Edad de la misma.

A continuación el código para cargar los datos y una muestra de las 6 primeras observaciones de la base de datos, en total tenemos 20 observaciones.

file <- "https://raw.githubusercontent.com/fhernanb/datos/master/propelente"
datos <- read.table(file=file, header=TRUE)
head(datos) # shows the first 6 rows

##   Resistencia  Edad
## 1     2158.70 15.50
## 2     1678.15 23.75
## 3     2316.00  8.00
## 4     2061.30 17.00
## 5     2207.50  5.50
## 6     1708.30 19.00

Para crear un diagrama de dispersión que nos muestre la relación entre las dos variables usamos las siguientes instrucciones.

library(ggplot2)
ggplot(datos, aes(x=Edad, y=Resistencia)) + 
  geom_point() + theme_light()

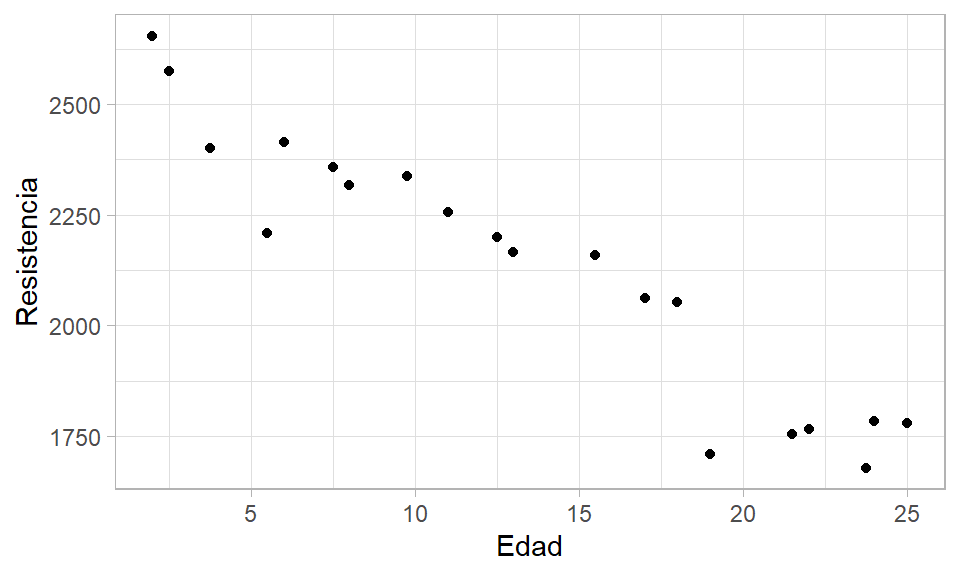
De la figura anterior se ve claramente que a medida que aumenta la edad de la soldadura, la resistencia que ella ofrece disminuye. Adicionalmente, se observa que la relación entre las variables es lineal con una dispersión que parece constante.

¿Quién estima mejor? ¿un modelo de regresión lineal simple o un árbol?

rls <- lm(Resistencia ~ Edad, data=datos)
arb <- rpart(Resistencia ~ Edad, data=datos)

arb <- rpart(Resistencia ~ Edad, data=datos, method="anova")

¿Qué hay dentro de modelo de regresión lineal simple?

summary(rls)

## 
## Call:
## lm(formula = Resistencia ~ Edad, data = datos)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -215.98  -50.68   28.74   66.61  106.76 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 2627.822     44.184   59.48  < 2e-16 ***
## Edad         -37.154      2.889  -12.86 1.64e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 96.11 on 18 degrees of freedom
## Multiple R-squared:  0.9018, Adjusted R-squared:  0.8964 
## F-statistic: 165.4 on 1 and 18 DF,  p-value: 1.643e-10

¿Qué hay dentro de modelo del arbol?

summary(arb)

## Call:
## rpart(formula = Resistencia ~ Edad, data = datos, method = "anova")
##   n= 20 
## 
##          CP nsplit rel error   xerror     xstd
## 1 0.7480619      0 1.0000000 1.184195 0.250625
## 2 0.0100000      1 0.2519381 1.184195 0.250625
## 
## Variable importance
## Edad 
##  100 
## 
## Node number 1: 20 observations,    complexity param=0.7480619
##   mean=2131.358, MSE=84686.88 
##   left son=2 (8 obs) right son=3 (12 obs)
##   Primary splits:
##       Edad < 16.25 to the right, improve=0.7480619, (0 missing)
## 
## Node number 2: 8 observations
##   mean=1823.094, MSE=19439.95 
## 
## Node number 3: 12 observations
##   mean=2336.867, MSE=22599.79

Construyamos nuevamente el árbol pero explorando todas las opciones de la función prp.

prp(arb, main = "",
    nn = TRUE,             # display the node numbers
    fallen.leaves = TRUE,  # put the leaves on the bottom of the page
    shadow.col = "gray",   # shadows under the leaves
    branch.lty = 3,        # draw branches using dotted lines
    branch = .5,           # change angle of branch lines
    faclen = 0,            # faclen = 0 to print full factor names
    trace = 1,             # print the auto calculated cex, xlim, ylim
    split.cex = 1.2,       # make the split text larger than the node text
    split.prefix = "is ",  # put "is " before split text
    split.suffix = "?",    # put "?" after split text
    split.box.col = "lightblue",   # lightgray split boxes (default is white)
    split.border.col = "darkgray", # darkgray border on split boxes
    split.round = 0.5)             # round the split box corners a tad

## cex 1   xlim c(-0.65, 1.65)   ylim c(-0.15, 1.15)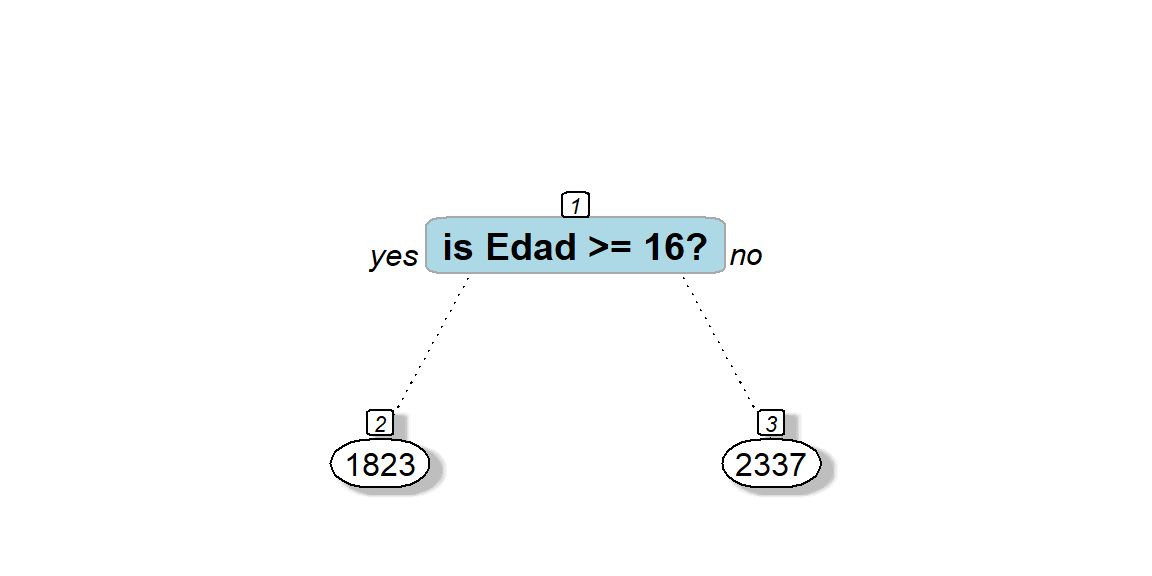

A continuación las predicciones con ambos modelos.

pred_rls <- predict(object=rls, newdata=datos)
pred_arb <- predict(object=arb, newdata=datos)

Dibujemos \(y_i\) versus \(\hat{y}_i\).

par(mfrow=c(1, 2))
plot(x=pred_rls, y=datos$Resistencia, main="RLS")
abline(a=0, b=1, lty="dashed", col="blue")
plot(x=pred_arb, y=datos$Resistencia, main="Arbol")
abline(a=0, b=1, lty="dashed", col="blue")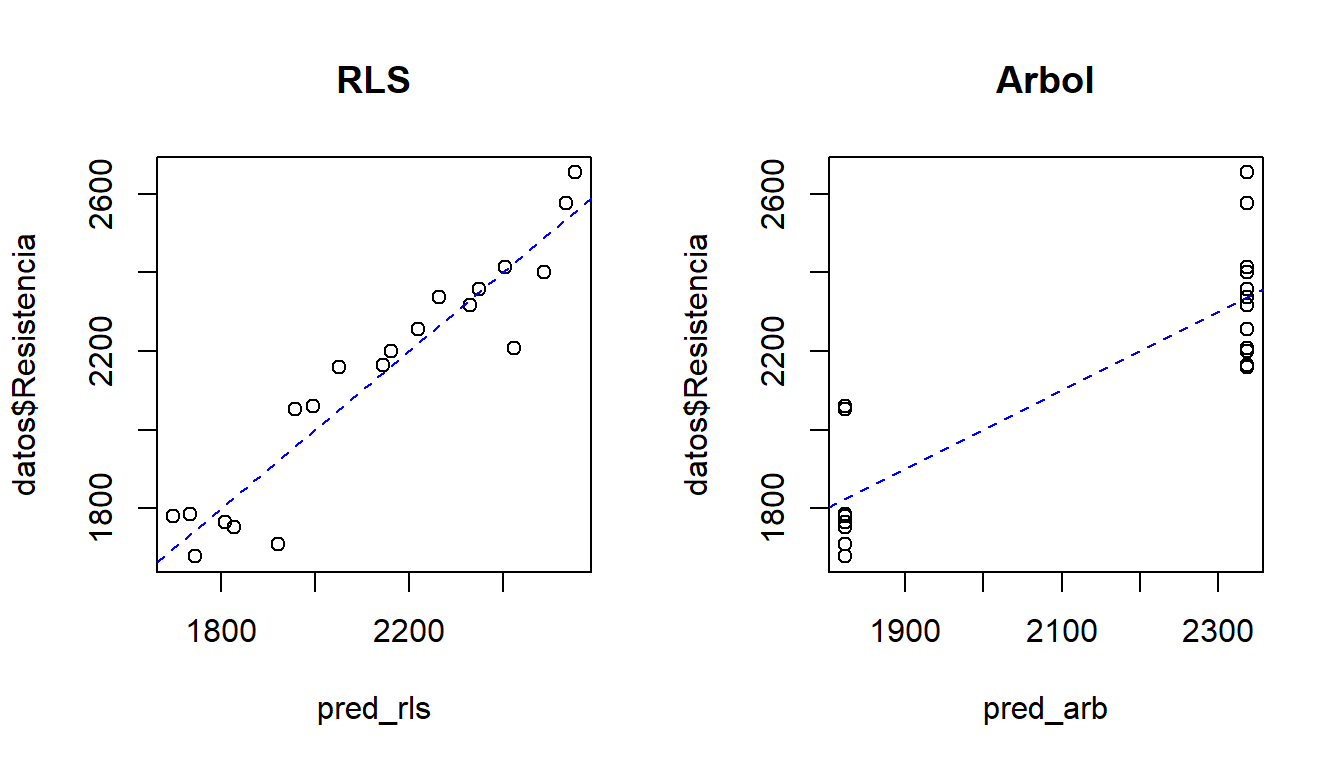

Vamos a calcular \(Cor(y_i, \hat{y}_i)\).

cor(datos$Resistencia, pred_rls)

## [1] 0.9496533

cor(datos$Resistencia, pred_arb)

## [1] 0.8649057

Calculemos ahora el Error Cuadrático Medio \(ECM=\frac{1}{n}\sum(y_i-\hat{y}_i)^2\).

mean((datos$Resistencia - pred_rls)^2)

## [1] 8312.743

mean((datos$Resistencia - pred_arb)^2)

## [1] 21335.85

¿Cuál método prefiere usted?

Estudio de simulación para comparar ambos métodos

El objetivo es comparar ambos modelos repetidas veces, para esto vamos a simular conjuntos de datos que tengan un comportamiento lineal y parecido a los datos del ejemplo. El modelo que vamos a considerar es el siguiente:

\[\begin{align} y_i &\sim N(\mu_i, \sigma^2), \\ \mu_i &= 2627 - 37 x_i, \\ \sigma &= 96, \\ x &\sim U(2, 25) \end{align}\]

Vamos a crear una función generadora de datos.

gen_dat <- function(n) {
  x <- runif(n=n, min=2, max=25)
  media <- 2627 - 37 * x
  y <- rnorm(n=n, mean=media, sd=96)
  data.frame(x=x, y=y)
}

Generemos unos datos de prueba y graficamos los datos.

datos_train <- gen_dat(n=20)
ggplot(datos_train, aes(x=x, y=y)) + 
  geom_point() + theme_light()

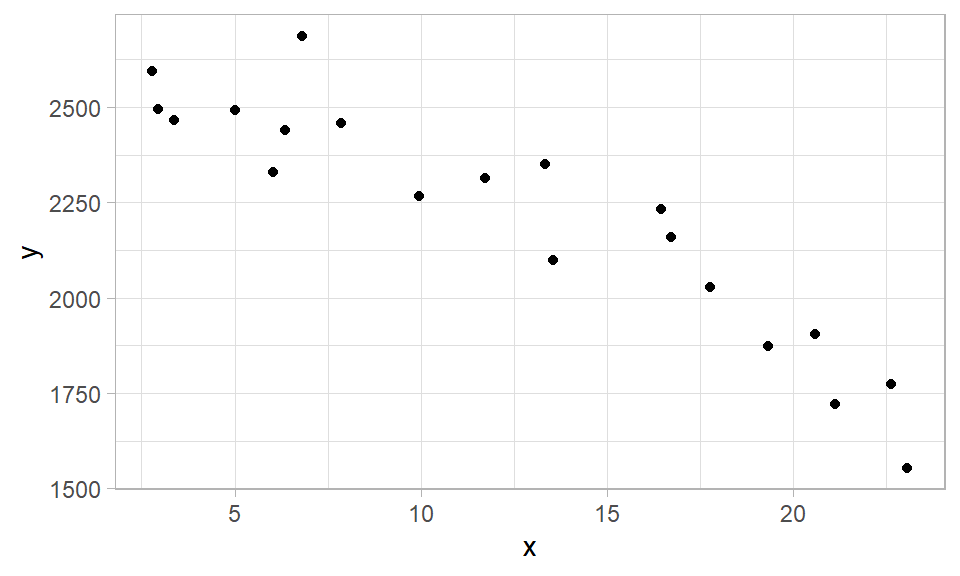
Usando los datos de prueba vamos a ajustar los modelos y luego calcularemos los indicadores.

datos_train <- gen_dat(n=20)  # Para entrenar
datos_test  <- gen_dat(n=20)  # Para validar
rls <- lm(y ~ x, data=datos_train)
arb <- rpart(y ~ x, data=datos_train)
pred_rls <- predict(object=rls, newdata=datos_test)
pred_arb <- predict(object=arb, newdata=datos_test)
cor(datos_test$y, pred_rls)

## [1] 0.9531806

cor(datos_test$y, pred_arb)

## [1] 0.8176202

mean((datos_test$y - pred_rls)^2)

## [1] 7951.993

mean((datos_test$y - pred_arb)^2)

## [1] 32835.24

Al observar los resultados anteriores vemos que el modelo de regresión lineal se comporta mejor que el árbol de regresión, esto se debe a que los datos están siendo generados con un modelo de regresión lineal.

Ahora vamos a realizar el estudio de simulación para explorar el efecto de \(n = 10, 20, 40\) sobre el \(ECM\) usando 5 réplicas para cada \(n\), este es un estudio de simulación “naive” pero ilustrativo.

n <- c(10, 20, 40)
nrep <- 5
result <- numeric()
for (i in n) {
  for(k in 1:nrep) {
    datos_train <- gen_dat(n=i)  # Para entrenar
    datos_test  <- gen_dat(n=i)  # Para validar
    rls <- lm(y ~ x, data=datos_train)
    arb <- rpart(y ~ x, data=datos_train)
    pred_rls <- predict(object=rls, newdata=datos_test)
    pred_arb <- predict(object=arb, newdata=datos_test)
    ecm1 <- mean((datos_test$y - pred_rls)^2)
    ecm2 <- mean((datos_test$y - pred_arb)^2)
    result <- rbind(result, c(i, ecm1, ecm2)) # No eficiente pero sirve
  }
}
colnames(result) <- c("n", "ecm_lrs", "ecm_arb")
result <- as.data.frame(result)
result

##     n   ecm_lrs   ecm_arb
## 1  10 11561.409  45829.58
## 2  10  5941.793  43297.25
## 3  10 25397.007 111663.54
## 4  10 12409.682  71720.23
## 5  10 15095.712  44398.16
## 6  20 10160.895  22593.85
## 7  20  7179.949  28906.90
## 8  20  6170.543  39031.82
## 9  20 11935.307  28125.38
## 10 20 11718.410  22418.01
## 11 40  9400.226  19430.35
## 12 40  6962.714  23450.19
## 13 40 10313.839  20534.37
## 14 40  8308.219  11837.12
## 15 40  7127.208  19337.81

El objeto result tiene los resultados de la simulación, vamos a calcular el \(ECM\) promedio para rls y árboles diferenciando por \(n\).

library(dplyr)
result %>% group_by(n) %>% summarise(ecm_medio_lrs=mean(ecm_lrs),
                                     ecm_medio_arb=mean(ecm_arb))

## # A tibble: 3 × 3
##       n ecm_medio_lrs ecm_medio_arb
##   <dbl>         <dbl>         <dbl>
## 1    10        14081.        63382.
## 2    20         9433.        28215.
## 3    40         8422.        18918.

Retos

A continuación los retos que usted debe aceptar.

Extienda el estudio de simulación para otros valores de \(n\) y aumentando el número de repeticiones nrep, decida usted los valores.
Con los resultados anteriores haga un gráfico de \(ECM\) promedio versus \(n\) para rls y árboles en la misma figura.
¿Se iguala \(ECM\) promedio del árbol con el de regresión para algún valor de \(n\)?
¿Cuál técnica presenta el \(ECM\) menor?
¿Es posible encontrar un \(ECM=0\) para algún valor de \(n\)?
¿Para qué sirve el paquete dplyr?
¿Qué es un tibble?