8 Gradient Boost

Gradient Boost fue propuesto por Friedman (1999a) y Friedman (1999b) y consiste en crear varios predictores en secuencia. El primer predictor usa la media de la variable \(Y\) para predecir, luego el segundo predictor explica los errores del primer predictor, el tercer predictor explicar los erroes del segundo predictor y así sucesivamente. En la siguiente figura se muestra una ilustración de lo que es Gradient Boost.

Ejemplo

Abajo se presenta un video con una explicación detallada de lo que es Gradient Boost.

Ejemplo

En este ejemplo se muestra como aplicar Gradient Boost de forma manual usando los datos del video anterior.

height <- c(1.6, 1.6, 1.5, 1.8, 1.5, 1.4)
color <- c("blue", "green", "blue", "red", "green", "blue")
gender <- c("male", "female", "female", "male", "male", "female")
weigth <- c(88, 76, 56, 73, 77, 57)

La librería para crear los árboles será rpart.

library(rpart)

El valor learning rate en el ejemplo será \(\alpha=0.10\). A continuación el código para crear el modelo inicial y los modelos siguientes del video anterior.

a <- 0.1 # Learning rate

# Modelo inicial
res1 <- weigth - mean(weigth)

# Modelo 2
mod2 <- rpart(res1 ~ height + color + gender,
              control=rpart.control(minsplit = 3))
res2 <- weigth - (mean(weigth) + a * predict(mod2))

# Modelo 3
mod3 <- rpart(res2 ~ height + color + gender,
              control=rpart.control(minsplit = 3))
res3 <- weigth - (mean(weigth) + a * predict(mod2) + a * predict(mod3))

A continuación una tabla con los residuales de los modelos.

cbind(res1, res2, res3)

##         res1   res2    res3
## 1  16.833333  15.15  13.635
## 2   4.833333   4.35   3.915
## 3 -15.166667 -13.70 -12.380
## 4   1.833333   1.45   1.105
## 5   5.833333   5.45   5.105
## 6 -14.166667 -12.70 -11.380

Para predecir el valor de weigth cuando height=1.7, color=“green” y gender=“male” se usa el siguiente código.

new_data <- data.frame(height=1.7, color="green", gender="female")
mean(weigth) + a * predict(mod2, new_data) + a * predict(mod3, new_data)

##      1 
## 72.085

Ejemplo

En este ejemplo se van a usar los datos Boston del paquete MASS de Ripley (2024) para predecir la variable medv en función de las otras covariables.

Para explorar la base de datos usamos el siguiente código.

library(MASS)
str(Boston)

## 'data.frame':    506 obs. of  14 variables:
##  $ crim   : num  0.00632 0.02731 0.02729 0.03237 0.06905 ...
##  $ zn     : num  18 0 0 0 0 0 12.5 12.5 12.5 12.5 ...
##  $ indus  : num  2.31 7.07 7.07 2.18 2.18 2.18 7.87 7.87 7.87 7.87 ...
##  $ chas   : int  0 0 0 0 0 0 0 0 0 0 ...
##  $ nox    : num  0.538 0.469 0.469 0.458 0.458 0.458 0.524 0.524 0.524 0.524 ...
##  $ rm     : num  6.58 6.42 7.18 7 7.15 ...
##  $ age    : num  65.2 78.9 61.1 45.8 54.2 58.7 66.6 96.1 100 85.9 ...
##  $ dis    : num  4.09 4.97 4.97 6.06 6.06 ...
##  $ rad    : int  1 2 2 3 3 3 5 5 5 5 ...
##  $ tax    : num  296 242 242 222 222 222 311 311 311 311 ...
##  $ ptratio: num  15.3 17.8 17.8 18.7 18.7 18.7 15.2 15.2 15.2 15.2 ...
##  $ black  : num  397 397 393 395 397 ...
##  $ lstat  : num  4.98 9.14 4.03 2.94 5.33 ...
##  $ medv   : num  24 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 ...

Vamos a crear dos conjuntos de datos, uno de entrenamiento y otro de validación de la siguiente manera.

library(caret)
set.seed(123)
indexes <- createDataPartition(Boston$medv, p = .90, list = F)
train <- Boston[indexes, ]
test <- Boston[-indexes, ]

El primer modelo predictivo será un árbol sencillo que nos servirá como elemento de comparación.

library(rpart)
model_tree <- rpart(medv ~ ., data=train)

Ahora vamos a calcular el \(RMSE\) (root mean square error) y la correlación entre \(y\) y \(\hat{y}\).

y_hat <- predict(model_tree)
sqrt(sum((train$medv - y_hat)^2))

## [1] 83.63843

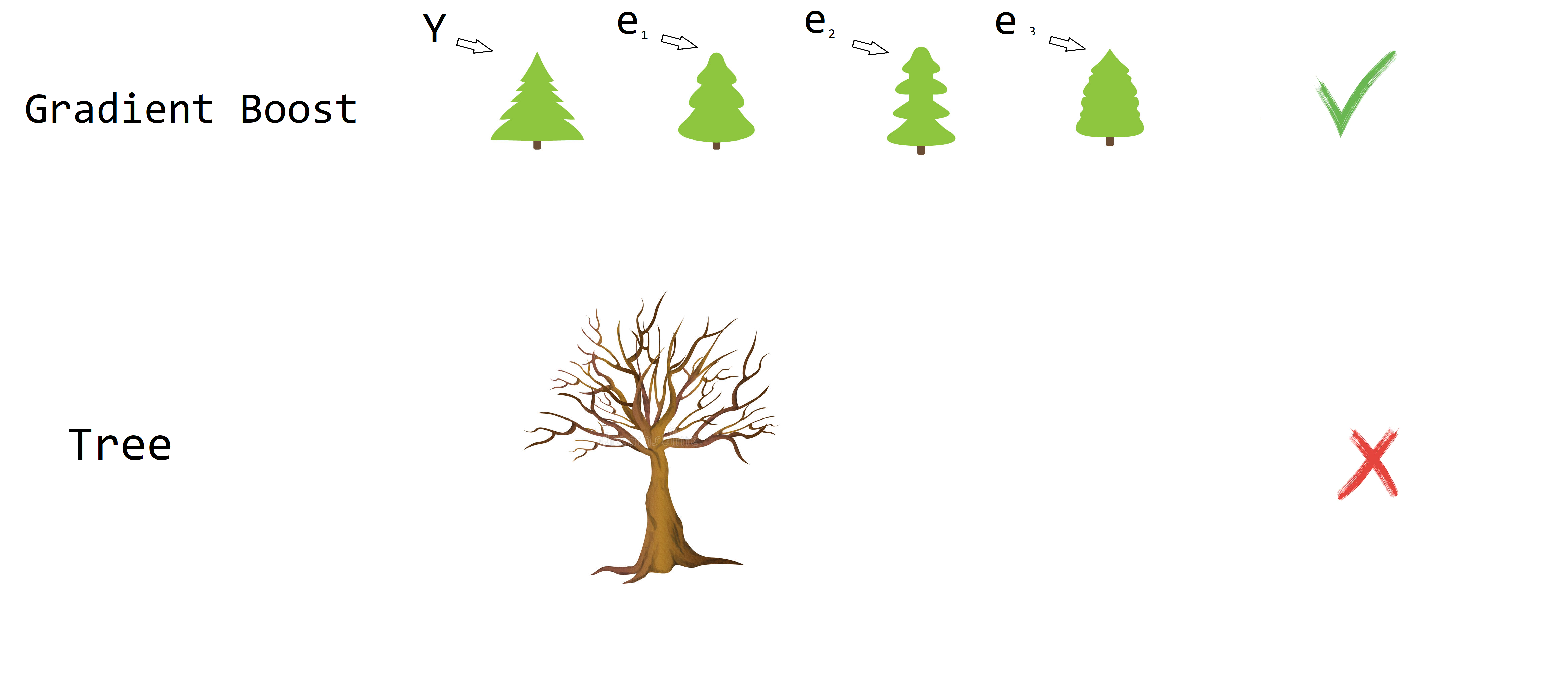
cor(train$medv, y_hat)

## [1] 0.9070587

Para comparar los resultados del modelo vamos a crear un diagrama de dispersión entre \(y\) y \(\hat{y}\).

plot(x=train$medv, y=y_hat, xlab='Valor observado', ylab='Predicción')
abline(a=0, b=1, lty='dashed')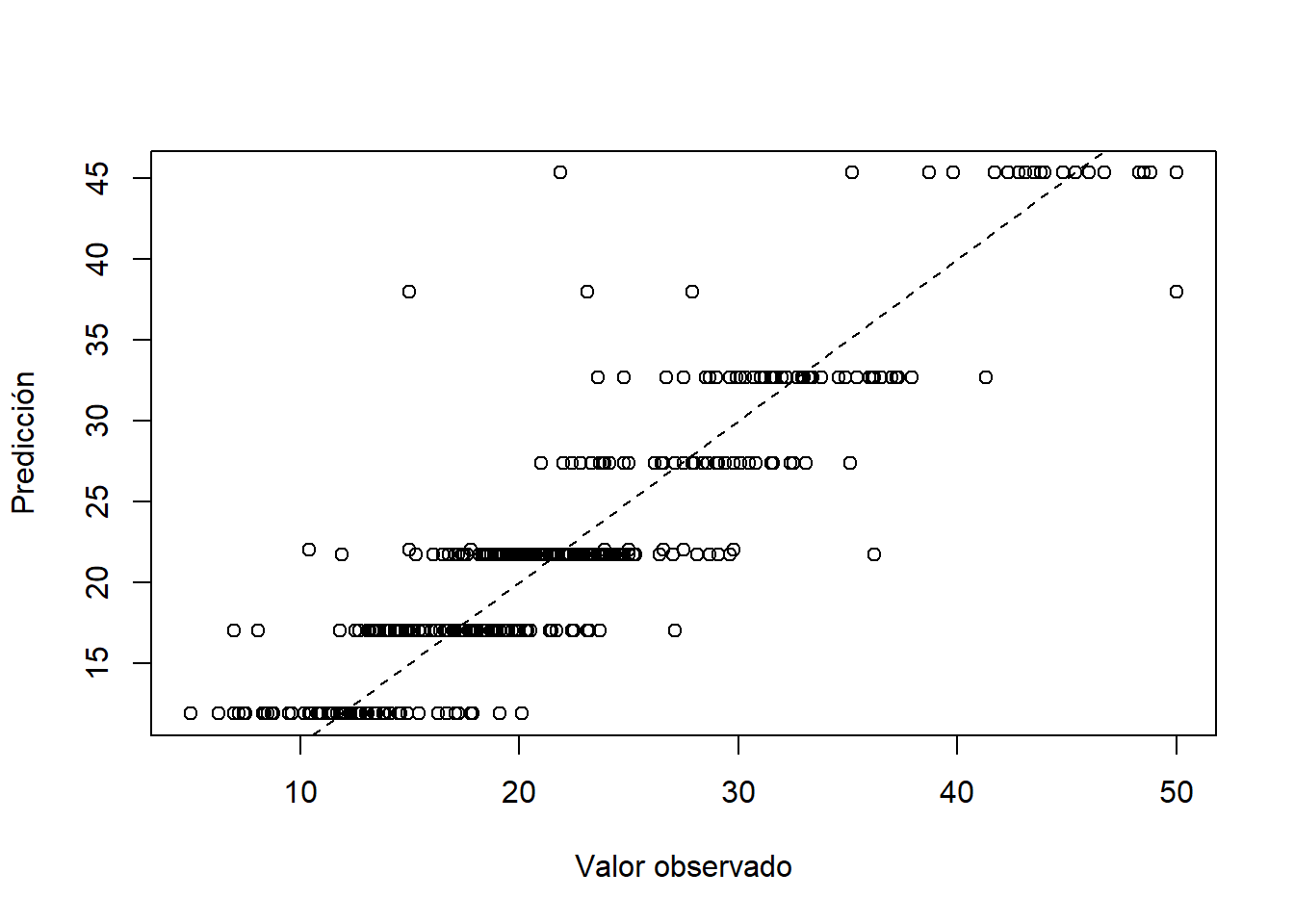

Ahora vamos a usar la función gbm del paquete de Greg and Developers (2024) para aplicar el algoritmo Gradient Boost con \(\alpha=0.01\), 5000 árboles (iteraciones) y una profundidad de 1 en cada árbol (stump).

library(gbm)
set.seed(123) # for reproducibility
model_gbm1 <- gbm(medv ~., data = train,
                  distribution="gaussian", cv.folds=5, 
                  shrinkage=0.01, n.minobsinnode=10,
                  n.trees=5000, interaction.depth=1)
print(model_gbm1)

## gbm(formula = medv ~ ., distribution = "gaussian", data = train, 
##     n.trees = 5000, interaction.depth = 1, n.minobsinnode = 10, 
##     shrinkage = 0.01, cv.folds = 5)
## A gradient boosted model with gaussian loss function.
## 5000 iterations were performed.
## The best cross-validation iteration was 4404.
## There were 13 predictors of which 13 had non-zero influence.

Ahora vamos a calcular el \(RMSE\) (root mean square error) y la correlación entre \(y\) y \(\hat{y}\).

sqrt(min(model_gbm1$cv.error))

## [1] 3.636371

y_hat <- predict(model_gbm1)

## Using 4404 trees...

cor(train$medv, y_hat)

## [1] 0.9542746

Para comparar los resultados del modelo vamos a crear un diagrama de dispersión entre \(y\) y \(\hat{y}\).

plot(x=train$medv, y=y_hat, xlab='Valor observado', ylab='Predicción')
abline(a=0, b=1, lty='dashed')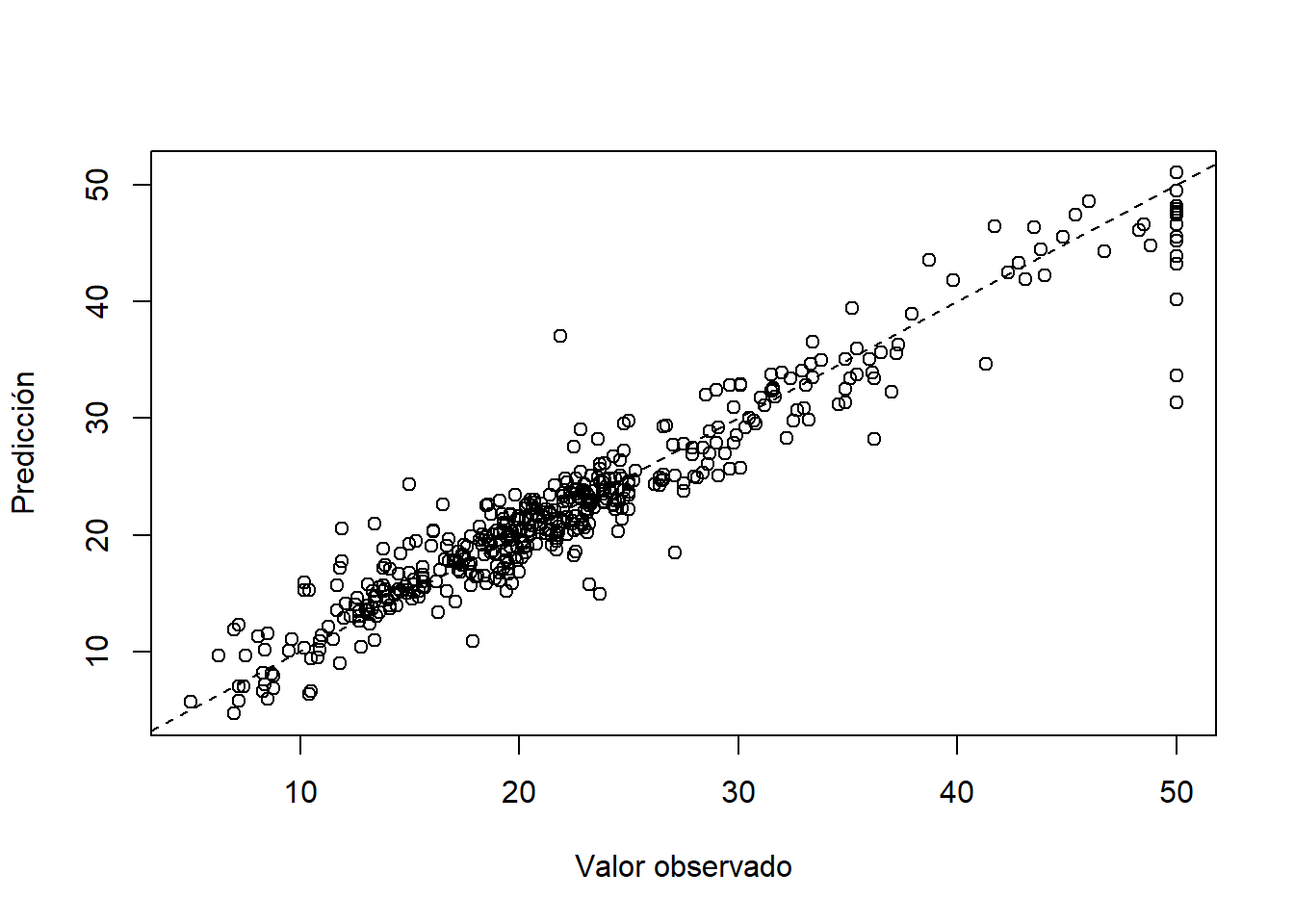

Al comparar la correlación y los diagramas de dispersión se observa una mejora considerable con el modelo Gradient Boost.

Podemos construir una figura para observar la evolución del \(RMSE\) en función del número de árboles (iteraciones).

gbm.perf(model_gbm1, method = "cv")

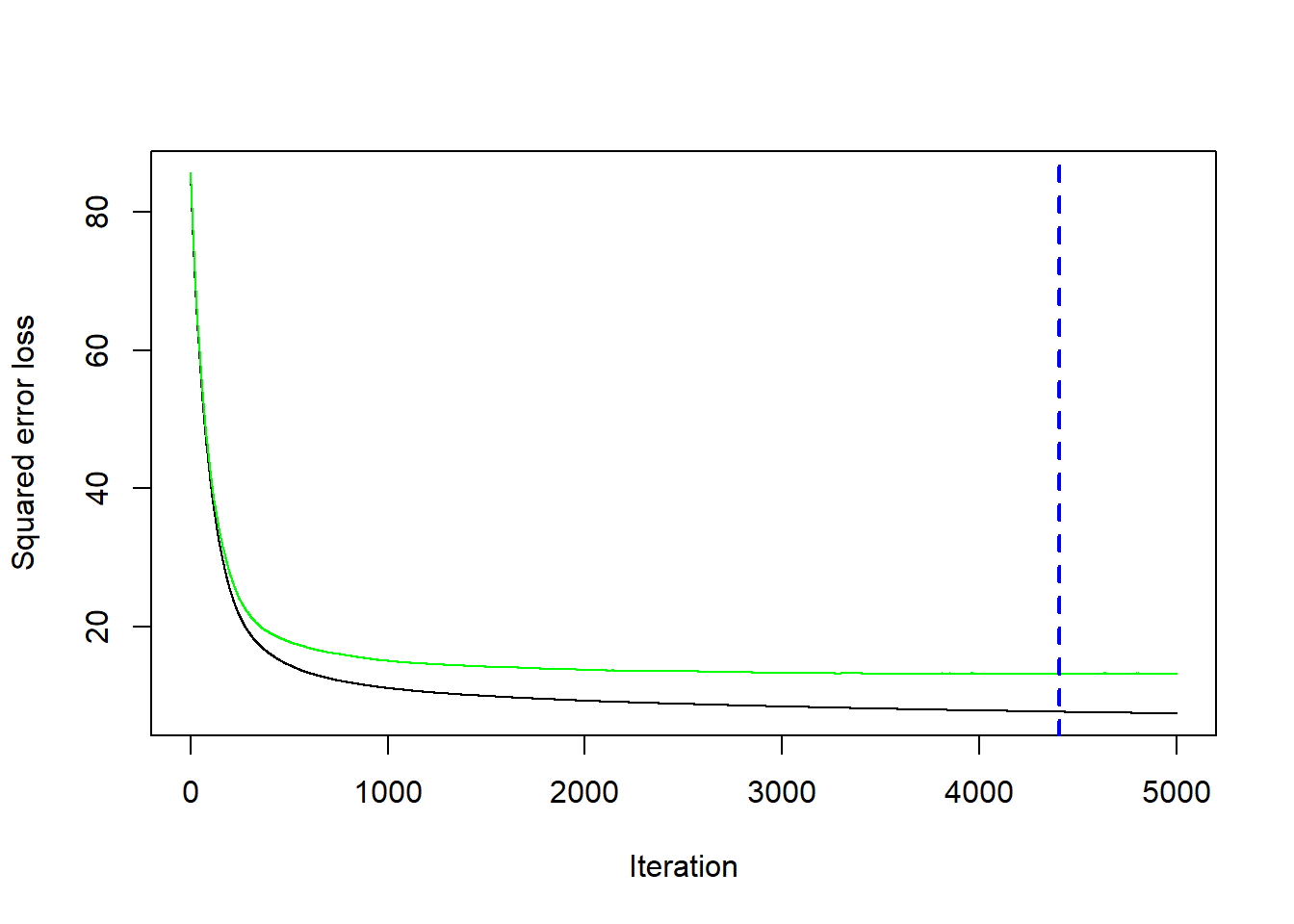
## [1] 4404

De la figura anterior se observa que en la iteración 4404 (linea azul a trazos) fue donde se obtuvo el menor \(RMSE\).

Vamos a crear otro modelo de predicción pero cambiando algunos de los hiper-parámetros, \(\alpha=0.15\) y una profundidad de 3 en cada árbol.

set.seed(123)
model_gbm2 <- gbm(medv ~., data = train,
                  distribution="gaussian", cv.folds=5, 
                  shrinkage=0.15, n.minobsinnode=10,
                  n.trees=5000, interaction.depth=3)

Ahora vamos a calcular el \(RMSE\) (root mean square error) y la correlación entre \(y\) y \(\hat{y}\).

sqrt(min(model_gbm2$cv.error))

## [1] 3.370139

y_hat <- predict(model_gbm2)

## Using 241 trees...

cor(train$medv, y_hat)

## [1] 0.9852213

Para comparar los resultados del modelo vamos a crear un diagrama de dispersión entre \(y\) y \(\hat{y}\).

plot(x=train$medv, y=y_hat, xlab='Valor observado', ylab='Predicción')
abline(a=0, b=1, lty='dashed')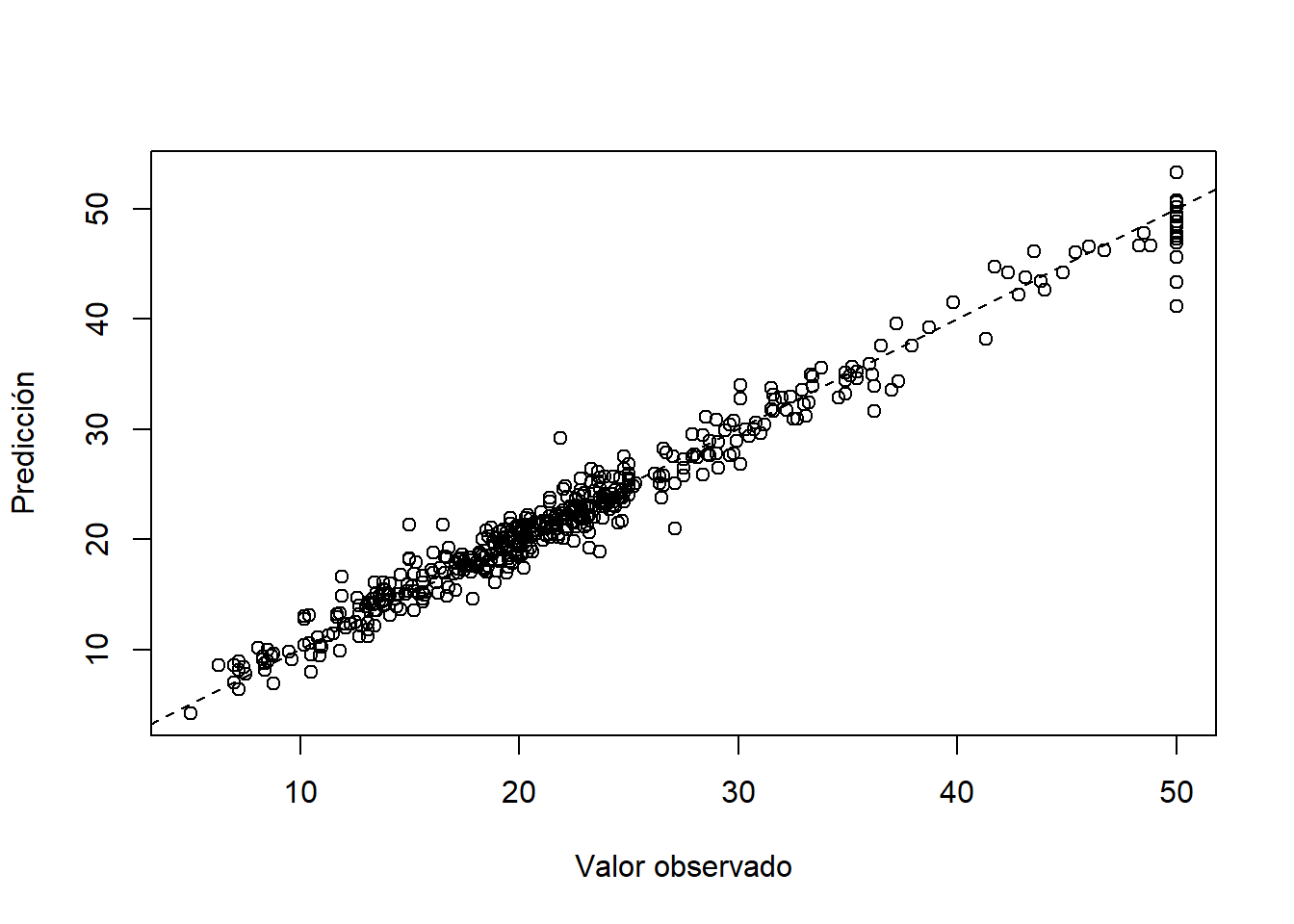

Podemos construir una figura para observar la evolución del \(RMSE\) en función del número de árboles (iteraciones).

gbm.perf(model_gbm2, method = "cv")

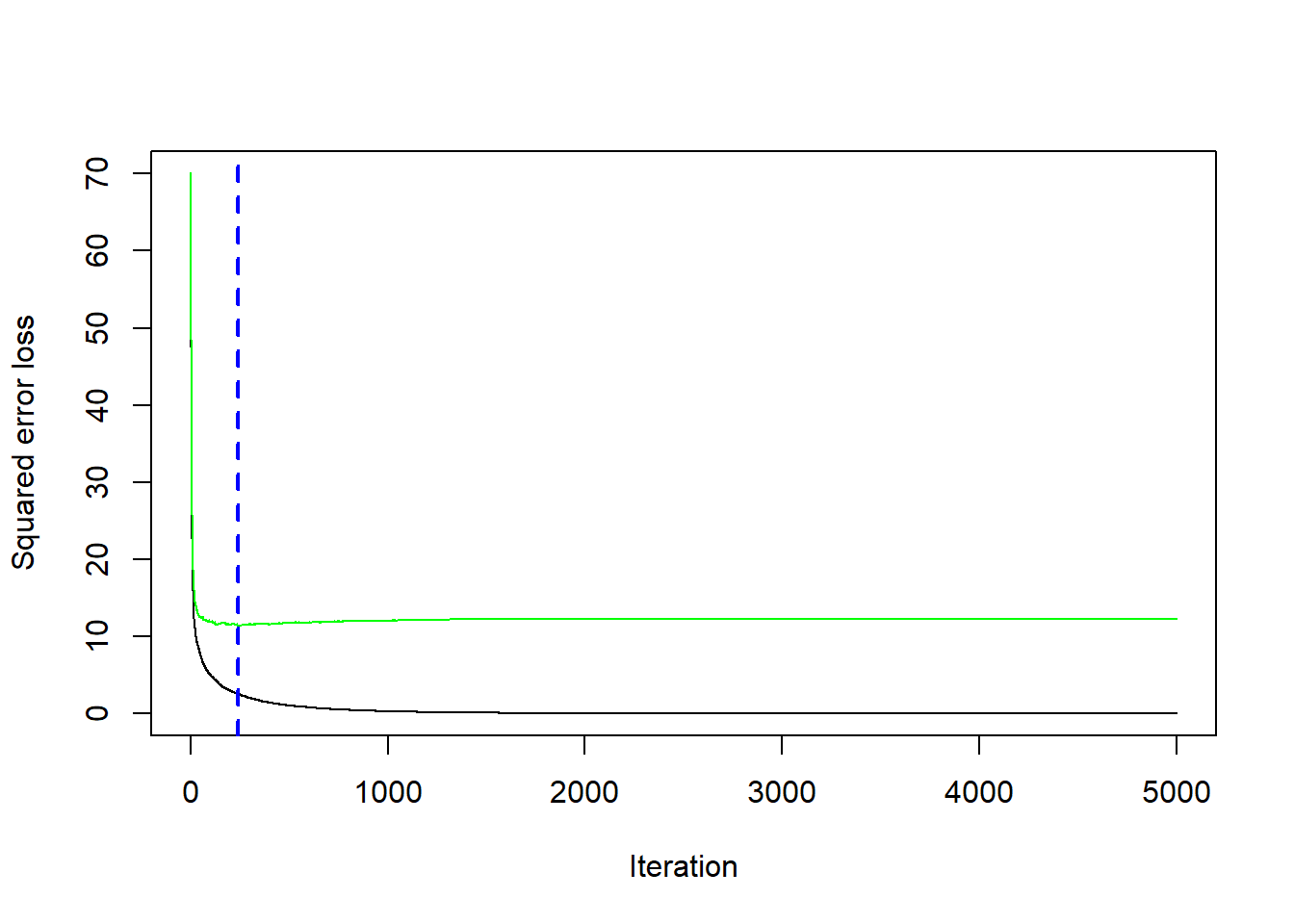
## [1] 241

En lugar de buscar esos hiper-parámetros a manualmente, podemos hacer una búsqueda automática creando un conjunto de posibles valores de los hiper-parámetros así.

# create hyperparameter grid
hyper_grid <- expand.grid(
  shrinkage = c(0.01, 0.1, 0.3),
  interaction.depth = c(1, 3, 5),
  n.minobsinnode = c(5, 10, 15),
  bag.fraction = c(0.65, 0.8, 1), 
  optimal_trees = 0,               # a place to dump results
  min_RMSE = 0,                    # a place to dump results
  min_cor = 0
)

nrow(hyper_grid) # total number of combinations

## [1] 81

Para hacer la búsqueda usamos el siguiente código.

# randomize data
random_index <- sample(1:nrow(train), nrow(train))
random_train <- train[random_index, ]

for(i in 1:nrow(hyper_grid)) {
  set.seed(123)
  gbm.tune <- gbm(
    formula = medv ~ .,
    distribution = "gaussian",
    data = random_train,
    n.trees = 5000,
    interaction.depth = hyper_grid$interaction.depth[i],
    shrinkage = hyper_grid$shrinkage[i],
    n.minobsinnode = hyper_grid$n.minobsinnode[i],
    bag.fraction = hyper_grid$bag.fraction[i],
    train.fraction = 0.75,
    n.cores = NULL, # will use all cores by default
    verbose = FALSE
  )
  
  # agregando la inf que nos interesa
  hyper_grid$optimal_trees[i] <- which.min(gbm.tune$valid.error)
  hyper_grid$min_RMSE[i] <- sqrt(min(gbm.tune$valid.error))
  hyper_grid$min_cor[i] <- cor(random_train$medv, predict(gbm.tune))
}

Organizamos los resultados en relación al menor \(RMSE\).

library(dplyr)
hyper_grid %>% 
  dplyr::arrange(min_RMSE) %>%
  head(10)

##    shrinkage interaction.depth n.minobsinnode bag.fraction optimal_trees
## 1       0.30                 5              5         0.80            88
## 2       0.30                 5              5         0.65           127
## 3       0.01                 5              5         0.80          3019
## 4       0.01                 3              5         0.65          4897
## 5       0.01                 5              5         0.65          4137
## 6       0.10                 5              5         1.00           128
## 7       0.01                 3              5         0.80          4884
## 8       0.01                 5              5         1.00          2543
## 9       0.01                 3             10         0.80          4984
## 10      0.01                 5             10         0.80          3699
##    min_RMSE   min_cor
## 1  2.685273 0.9862784
## 2  2.729782 0.9869481
## 3  2.778927 0.9869945
## 4  2.782291 0.9853981
## 5  2.796934 0.9876546
## 6  2.800982 0.9803835
## 7  2.837197 0.9852038
## 8  2.837520 0.9855254
## 9  2.860405 0.9838807
## 10 2.870885 0.9860587

# for reproducibility
set.seed(123)

# train GBM model
gbm.fit.final <- gbm(
  formula = medv ~ .,
  distribution = "gaussian",
  data = train,
  n.trees = 88,
  interaction.depth = 5,
  shrinkage = 0.3,
  n.minobsinnode = 5,
  bag.fraction = 0.80, 
  train.fraction = 1,
  n.cores = NULL, # will use all cores by default
  verbose = FALSE
  ) 

summary(gbm.fit.final, cBars = 10,
        method = relative.influence, las = 2)

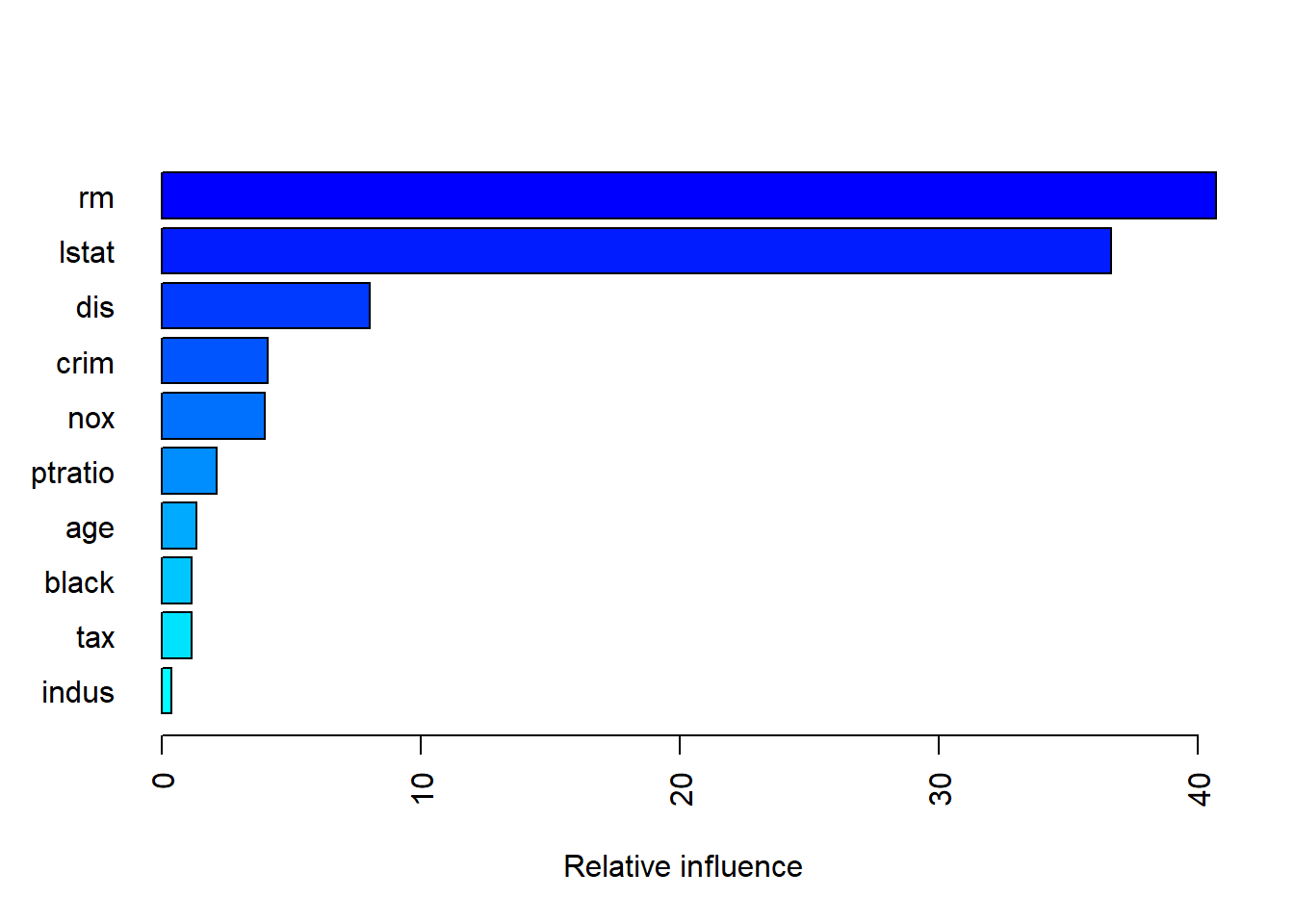
##             var     rel.inf
## rm           rm 40.70059606
## lstat     lstat 36.67225822
## dis         dis  8.03512644
## crim       crim  4.10937068
## nox         nox  3.99034366
## ptratio ptratio  2.13830279
## age         age  1.34811594
## black     black  1.16184689
## tax         tax  1.14437416
## indus     indus  0.37045656
## rad         rad  0.21608957
## zn           zn  0.07111692
## chas       chas  0.04200211

http://uc-r.github.io/gbm_regression

y_hat <- predict(object=gbm.fit.final, 
                 newdata=test, n.trees = 88)
cor(test$medv, y_hat)

## [1] 0.934735

plot(x=test$medv, y=y_hat, xlab='Valor observado', ylab='Predicción')
abline(a=0, b=1, lty='dashed')

References

Friedman, J. H. 1999a. “Greedy Function Approximation: A Gradient Boosting Machine.” Stanford University.

———. 1999b. “Stochastic Gradient Boosting.” Stanford University.

Greg, Ridgeway, and GBM Developers. 2024. Gbm: Generalized Boosted Regression Models. https://github.com/gbm-developers/gbm.

———. 2024. MASS: Support Functions and Datasets for Venables and Ripley’s MASS. http://www.stats.ox.ac.uk/pub/MASS4/.