Plot for confidence interval p - coverage vs n for fixed p
Source:R/ci_p_coverage.R
ci_p_coverage_plot2.RdThis function plots the coverage for any confidence interval for p.
ci_p_coverage_plot2(
p = 0.5,
seq_n = seq(from = 10, to = 500, by = 10),
conf.level = 0.95,
intervalType = "wald",
plot = TRUE,
col = "deepskyblue2",
linecolor = "tomato",
...
)Arguments
- p
true proportion \(p\).
- seq_n
sequence with the values of sample size \(n\). By default is the sequence 10, 20, 30, ..., 480, 490, 500.
- conf.level
nominal confidence level for the returned confidence interval. By default is 0.95.
- intervalType
type of confidence interval, possible choices are listed in ci_p.
- plot
logical value to obtain the plot, TRUE by default.
- col
color for the coverage curve.
- linecolor
color for the line representing the conf.level.
- ...
further arguments and graphical parameters passed to plot function.
Value
A dataframe with Method, n, p and true coverage and the plot.
Details
This function was inspired by the binomTestCoveragePlot() function from conf package and Park & Leemis (2019).
References
Park, H., & Leemis, L. M. (2019). Ensemble confidence intervals for binomial proportions. Statistics in Medicine, 38(18), 3460-3475.
See also
ci_p.
Examples
ci_p_coverage_plot2(p=0.50,
conf.level=0.95,
intervalType="wald")
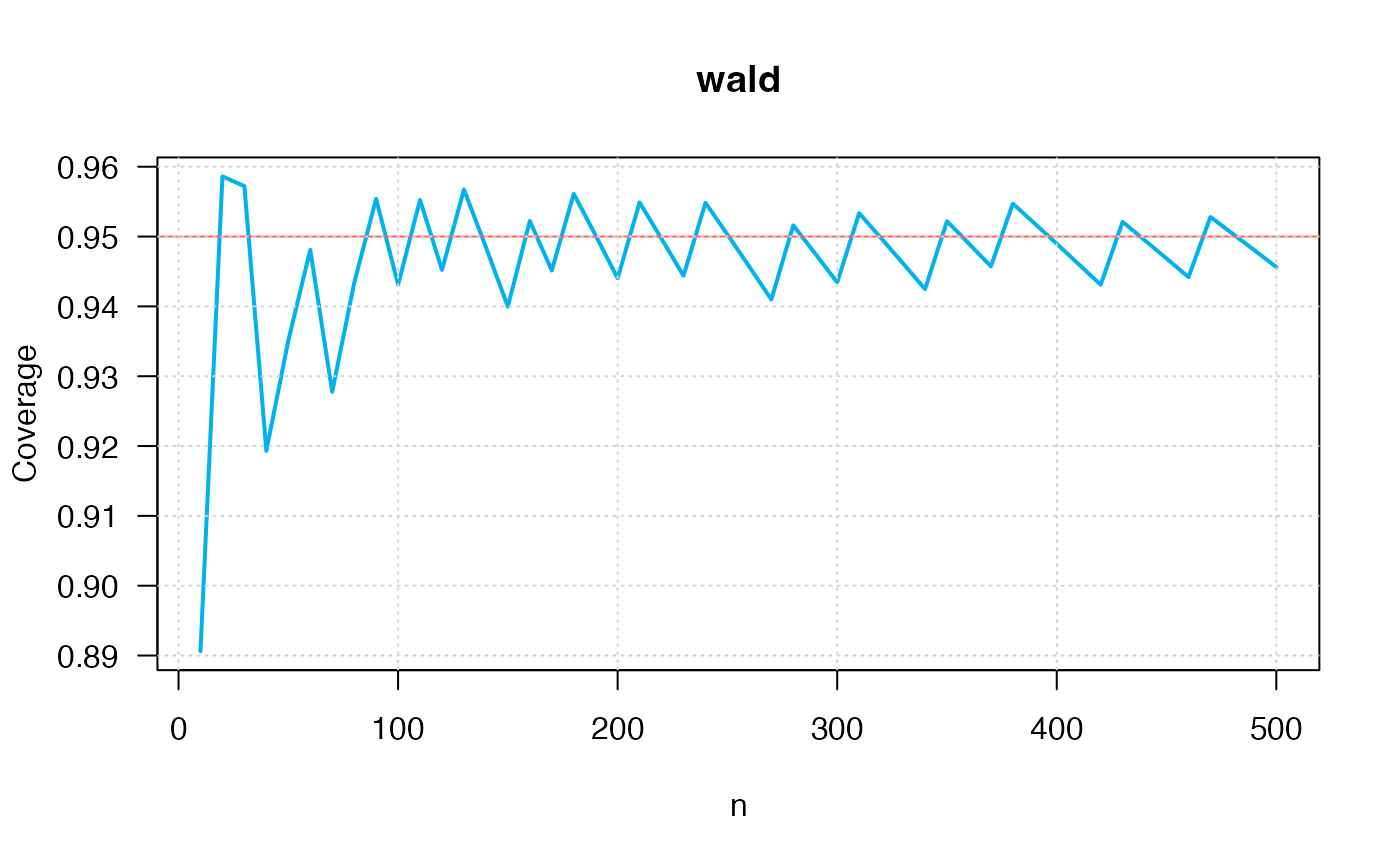#> intervalType n p coverage
#> 1 ci_p_wald 10 0.5 0.890625
#> 2 ci_p_wald 20 0.5 0.9586105
#> 3 ci_p_wald 30 0.5 0.9572261
#> 4 ci_p_wald 40 0.5 0.9193095
#> 5 ci_p_wald 50 0.5 0.9350914
#> 6 ci_p_wald 60 0.5 0.9481061
#> 7 ci_p_wald 70 0.5 0.9277621
#> 8 ci_p_wald 80 0.5 0.9433356
#> 9 ci_p_wald 90 0.5 0.9554025
#> 10 ci_p_wald 100 0.5 0.9431121
#> 11 ci_p_wald 110 0.5 0.9552379
#> 12 ci_p_wald 120 0.5 0.9452202
#> 13 ci_p_wald 130 0.5 0.9567449
#> 14 ci_p_wald 140 0.5 0.9484764
#> 15 ci_p_wald 150 0.5 0.9399728
#> 16 ci_p_wald 160 0.5 0.952233
#> 17 ci_p_wald 170 0.5 0.9451348
#> 18 ci_p_wald 180 0.5 0.956129
#> 19 ci_p_wald 190 0.5 0.9501486
#> 20 ci_p_wald 200 0.5 0.9440343
#> 21 ci_p_wald 210 0.5 0.9548859
#> 22 ci_p_wald 220 0.5 0.9496854
#> 23 ci_p_wald 230 0.5 0.9443864
#> 24 ci_p_wald 240 0.5 0.9548376
#> 25 ci_p_wald 250 0.5 0.9502932
#> 26 ci_p_wald 260 0.5 0.9456712
#> 27 ci_p_wald 270 0.5 0.9409868
#> 28 ci_p_wald 280 0.5 0.9515989
#> 29 ci_p_wald 290 0.5 0.9475432
#> 30 ci_p_wald 300 0.5 0.9434343
#> 31 ci_p_wald 310 0.5 0.9533484
#> 32 ci_p_wald 320 0.5 0.9497706
#> 33 ci_p_wald 330 0.5 0.9461461
#> 34 ci_p_wald 340 0.5 0.9424823
#> 35 ci_p_wald 350 0.5 0.9521962
#> 36 ci_p_wald 360 0.5 0.9489834
#> 37 ci_p_wald 370 0.5 0.9457345
#> 38 ci_p_wald 380 0.5 0.954713
#> 39 ci_p_wald 390 0.5 0.951853
#> 40 ci_p_wald 400 0.5 0.9489598
#> 41 ci_p_wald 410 0.5 0.9460373
#> 42 ci_p_wald 420 0.5 0.9430894
#> 43 ci_p_wald 430 0.5 0.9521066
#> 44 ci_p_wald 440 0.5 0.949493
#> 45 ci_p_wald 450 0.5 0.9468549
#> 46 ci_p_wald 460 0.5 0.9441951
#> 47 ci_p_wald 470 0.5 0.9527972
#> 48 ci_p_wald 480 0.5 0.9504289
#> 49 ci_p_wald 490 0.5 0.9480394
#> 50 ci_p_wald 500 0.5 0.945631
ci_p_coverage_plot2(p=0.75,
conf.level=0.95,
intervalType="wald")
#> intervalType n p coverage
#> 1 ci_p_wald 10 0.75 0.9239588
#> 2 ci_p_wald 20 0.75 0.8948752
#> 3 ci_p_wald 30 0.75 0.940957
#> 4 ci_p_wald 40 0.75 0.9451647
#> 5 ci_p_wald 50 0.75 0.9408265
#> 6 ci_p_wald 60 0.75 0.9394162
#> 7 ci_p_wald 70 0.75 0.9397955
#> 8 ci_p_wald 80 0.75 0.9412736
#> 9 ci_p_wald 90 0.75 0.943417
#> 10 ci_p_wald 100 0.75 0.945947
#> 11 ci_p_wald 110 0.75 0.9486811
#> 12 ci_p_wald 120 0.75 0.9514984
#> 13 ci_p_wald 130 0.75 0.9543188
#> 14 ci_p_wald 140 0.75 0.9489014
#> 15 ci_p_wald 150 0.75 0.9371451
#> 16 ci_p_wald 160 0.75 0.9417141
#> 17 ci_p_wald 170 0.75 0.9459686
#> 18 ci_p_wald 180 0.75 0.9499239
#> 19 ci_p_wald 190 0.75 0.9535965
#> 20 ci_p_wald 200 0.75 0.9369437
#> 21 ci_p_wald 210 0.75 0.9418286
#> 22 ci_p_wald 220 0.75 0.9463171
#> 23 ci_p_wald 230 0.75 0.9504435
#> 24 ci_p_wald 240 0.75 0.9542386
#> 25 ci_p_wald 250 0.75 0.9403776
#> 26 ci_p_wald 260 0.75 0.9450333
#> 27 ci_p_wald 270 0.75 0.9493047
#> 28 ci_p_wald 280 0.75 0.9532263
#> 29 ci_p_wald 290 0.75 0.9406335
#> 30 ci_p_wald 300 0.75 0.945252
#> 31 ci_p_wald 310 0.75 0.9494919
#> 32 ci_p_wald 320 0.75 0.9533865
#> 33 ci_p_wald 330 0.75 0.9419665
#> 34 ci_p_wald 340 0.75 0.9464353
#> 35 ci_p_wald 350 0.75 0.9505436
#> 36 ci_p_wald 360 0.75 0.9484632
#> 37 ci_p_wald 370 0.75 0.943968
#> 38 ci_p_wald 380 0.75 0.948227
#> 39 ci_p_wald 390 0.75 0.9521493
#> 40 ci_p_wald 400 0.75 0.9420098
#> 41 ci_p_wald 410 0.75 0.9463688
#> 42 ci_p_wald 420 0.75 0.9503889
#> 43 ci_p_wald 430 0.75 0.9486533
#> 44 ci_p_wald 440 0.75 0.9449082
#> 45 ci_p_wald 450 0.75 0.9489893
#> 46 ci_p_wald 460 0.75 0.9527597
#> 47 ci_p_wald 470 0.75 0.9437917
#> 48 ci_p_wald 480 0.75 0.9479041
#> 49 ci_p_wald 490 0.75 0.9517089
#> 50 ci_p_wald 500 0.75 0.9429725
ci_p_coverage_plot2(p=0.50,
conf.level=0.95,
intervalType="wilson")
#> intervalType n p coverage
#> 1 ci_p_wilson 10 0.5 0.9785156
#> 2 ci_p_wilson 20 0.5 0.9586105
#> 3 ci_p_wilson 30 0.5 0.9572261
#> 4 ci_p_wilson 40 0.5 0.9615227
#> 5 ci_p_wilson 50 0.5 0.9350914
#> 6 ci_p_wilson 60 0.5 0.9481061
#> 7 ci_p_wilson 70 0.5 0.9586086
#> 8 ci_p_wilson 80 0.5 0.9433356
#> 9 ci_p_wilson 90 0.5 0.9554025
#> 10 ci_p_wilson 100 0.5 0.9431121
#> 11 ci_p_wilson 110 0.5 0.9552379
#> 12 ci_p_wilson 120 0.5 0.9452202
#> 13 ci_p_wilson 130 0.5 0.9567449
#> 14 ci_p_wilson 140 0.5 0.9484764
#> 15 ci_p_wilson 150 0.5 0.9591315
#> 16 ci_p_wilson 160 0.5 0.952233
#> 17 ci_p_wilson 170 0.5 0.9451348
#> 18 ci_p_wilson 180 0.5 0.956129
#> 19 ci_p_wilson 190 0.5 0.9501486
#> 20 ci_p_wilson 200 0.5 0.9440343
#> 21 ci_p_wilson 210 0.5 0.9548859
#> 22 ci_p_wilson 220 0.5 0.9496854
#> 23 ci_p_wilson 230 0.5 0.9443864
#> 24 ci_p_wilson 240 0.5 0.9548376
#> 25 ci_p_wilson 250 0.5 0.9502932
#> 26 ci_p_wilson 260 0.5 0.9456712
#> 27 ci_p_wilson 270 0.5 0.9555904
#> 28 ci_p_wilson 280 0.5 0.9515989
#> 29 ci_p_wilson 290 0.5 0.9475432
#> 30 ci_p_wilson 300 0.5 0.9434343
#> 31 ci_p_wilson 310 0.5 0.9533484
#> 32 ci_p_wilson 320 0.5 0.9497706
#> 33 ci_p_wilson 330 0.5 0.9461461
#> 34 ci_p_wilson 340 0.5 0.9553674
#> 35 ci_p_wilson 350 0.5 0.9521962
#> 36 ci_p_wilson 360 0.5 0.9489834
#> 37 ci_p_wilson 370 0.5 0.9457345
#> 38 ci_p_wilson 380 0.5 0.954713
#> 39 ci_p_wilson 390 0.5 0.951853
#> 40 ci_p_wilson 400 0.5 0.9489598
#> 41 ci_p_wilson 410 0.5 0.9460373
#> 42 ci_p_wilson 420 0.5 0.9546927
#> 43 ci_p_wilson 430 0.5 0.9521066
#> 44 ci_p_wilson 440 0.5 0.949493
#> 45 ci_p_wilson 450 0.5 0.9468549
#> 46 ci_p_wilson 460 0.5 0.9551421
#> 47 ci_p_wilson 470 0.5 0.9527972
#> 48 ci_p_wilson 480 0.5 0.9504289
#> 49 ci_p_wilson 490 0.5 0.9480394
#> 50 ci_p_wilson 500 0.5 0.945631
ci_p_coverage_plot2(p=0.75,
conf.level=0.95,
intervalType="wilson",
col="orange", linecolor="purple")
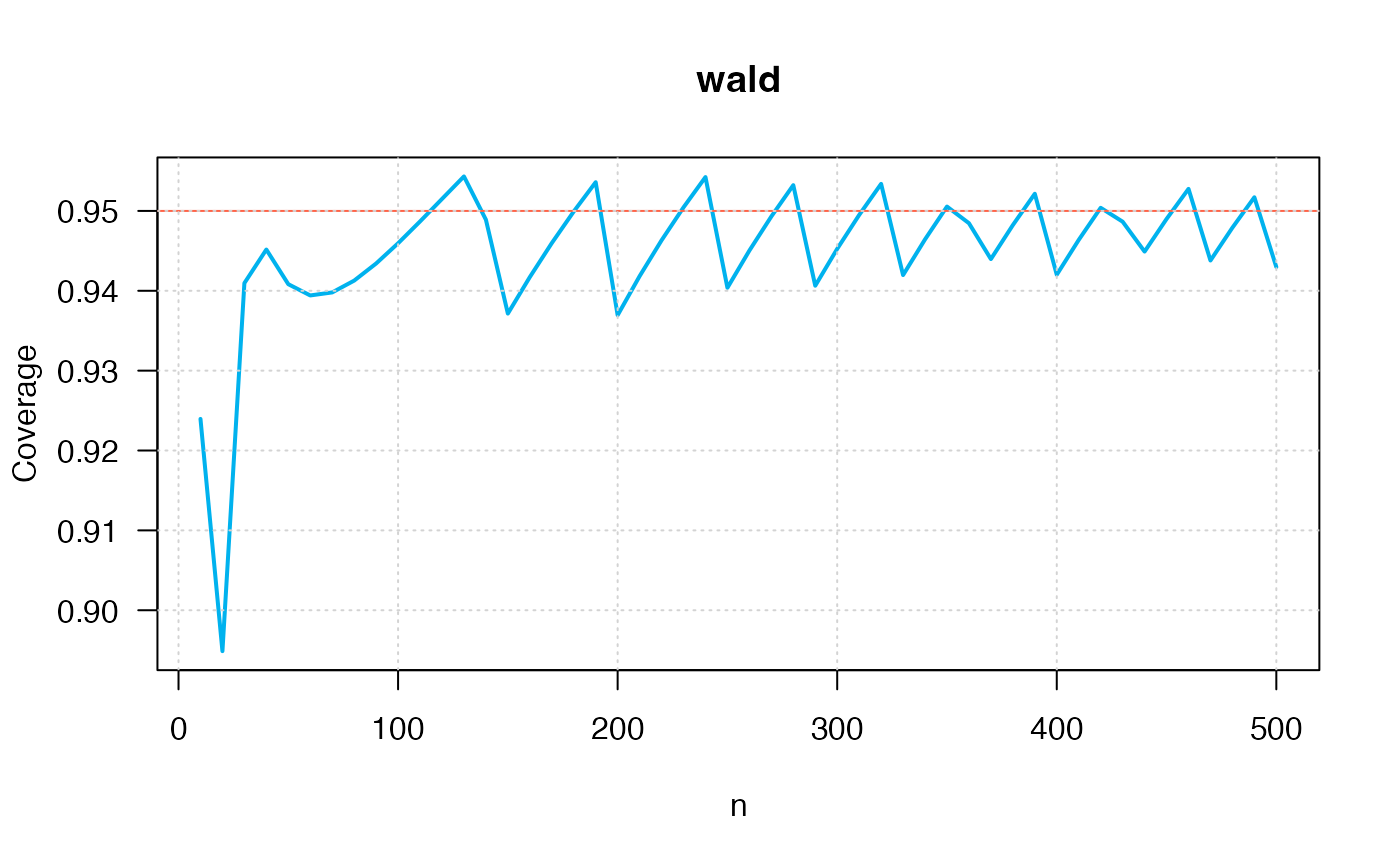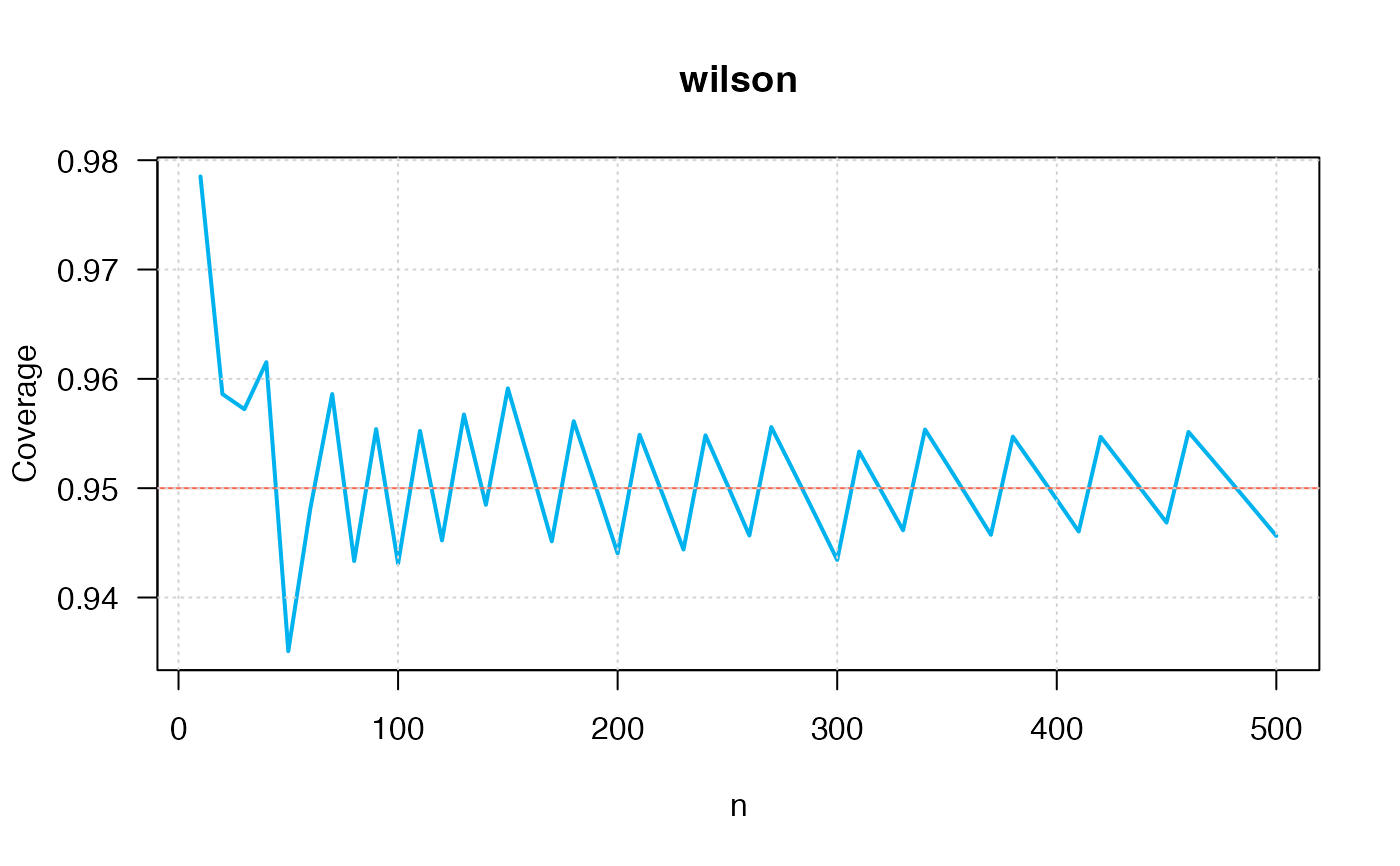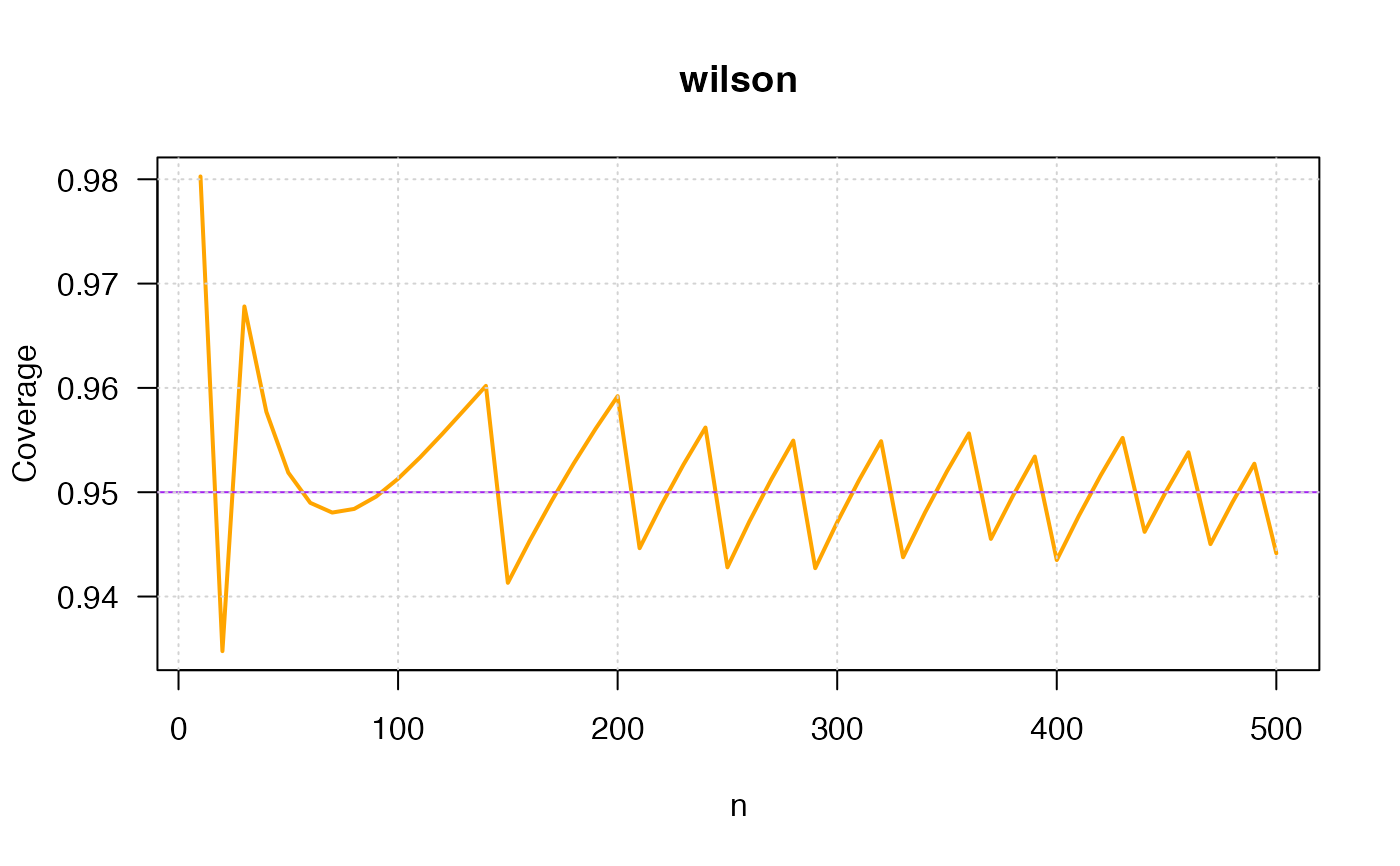#> intervalType n p coverage
#> 1 ci_p_wilson 10 0.75 0.9802723
#> 2 ci_p_wilson 20 0.75 0.9347622
#> 3 ci_p_wilson 30 0.75 0.9678105
#> 4 ci_p_wilson 40 0.75 0.9577129
#> 5 ci_p_wilson 50 0.75 0.951876
#> 6 ci_p_wilson 60 0.75 0.9489842
#> 7 ci_p_wilson 70 0.75 0.948049
#> 8 ci_p_wilson 80 0.75 0.948398
#> 9 ci_p_wilson 90 0.75 0.949581
#> 10 ci_p_wilson 100 0.75 0.9512948
#> 11 ci_p_wilson 110 0.75 0.9533335
#> 12 ci_p_wilson 120 0.75 0.9555561
#> 13 ci_p_wilson 130 0.75 0.9578659
#> 14 ci_p_wilson 140 0.75 0.9601959
#> 15 ci_p_wilson 150 0.75 0.9413114
#> 16 ci_p_wilson 160 0.75 0.9453706
#> 17 ci_p_wilson 170 0.75 0.949184
#> 18 ci_p_wilson 180 0.75 0.952756
#> 19 ci_p_wilson 190 0.75 0.9560945
#> 20 ci_p_wilson 200 0.75 0.9592093
#> 21 ci_p_wilson 210 0.75 0.9446319
#> 22 ci_p_wilson 220 0.75 0.948805
#> 23 ci_p_wilson 230 0.75 0.9526529
#> 24 ci_p_wilson 240 0.75 0.9562017
#> 25 ci_p_wilson 250 0.75 0.9427956
#> 26 ci_p_wilson 260 0.75 0.9471934
#> 27 ci_p_wilson 270 0.75 0.9512348
#> 28 ci_p_wilson 280 0.75 0.9549508
#> 29 ci_p_wilson 290 0.75 0.9427161
#> 30 ci_p_wilson 300 0.75 0.9471225
#> 31 ci_p_wilson 310 0.75 0.9511715
#> 32 ci_p_wilson 320 0.75 0.9548943
#> 33 ci_p_wilson 330 0.75 0.9437634
#> 34 ci_p_wilson 340 0.75 0.9480561
#> 35 ci_p_wilson 350 0.75 0.9520049
#> 36 ci_p_wilson 360 0.75 0.9556394
#> 37 ci_p_wilson 370 0.75 0.9455228
#> 38 ci_p_wilson 380 0.75 0.9496342
#> 39 ci_p_wilson 390 0.75 0.9534221
#> 40 ci_p_wilson 400 0.75 0.9434955
#> 41 ci_p_wilson 410 0.75 0.9477182
#> 42 ci_p_wilson 420 0.75 0.9516135
#> 43 ci_p_wilson 430 0.75 0.9552082
#> 44 ci_p_wilson 440 0.75 0.9461985
#> 45 ci_p_wilson 450 0.75 0.9501639
#> 46 ci_p_wilson 460 0.75 0.953828
#> 47 ci_p_wilson 470 0.75 0.9450232
#> 48 ci_p_wilson 480 0.75 0.9490282
#> 49 ci_p_wilson 490 0.75 0.952734
#> 50 ci_p_wilson 500 0.75 0.9441463