2 Gráficos para una variable cuantitativa

En este capítulo se presentan funciones para la creación de gráficos con una sola variable cuantitativa.

2.1 Función stem

Esta función permite crear el gráfico llamado de tallo y hoja. Este gráfico fue propuesto por Tukey (1977) y a pesar de no ser un gráfico para presentación definitiva, se utiliza a la vez que el analista recoge la información para ver rápidamente la distribución de los datos.

¿Qué muestra este gráfico?

1. El centro de la distribución.
2. La forma general de la distribución:
   • Simétrica: Si las porciones a cada lado del centro son imágenes espejos de las otras.
   • Sesgada a la izquierda: Si la cola izquierda (los valores menores) es mucho más larga que los de la derecha (los valores mayores).
   • Sesgada a la derecha: Opuesto a la sesgada a la izquierda.
3. Desviaciones marcadas de la forma global de la distribución.
   • Outliers: Observaciones individuales que caen muy por fuera del patrón general de los datos.
   • Gaps: Huecos en la distribución

Ventajas del gráfico:

1. Muy fácil de realizar y puede hacerse a mano.
2. Fácil de entender.

Desventajas del gráfico:

1. El gráfico es tosco y no sirve para presentaciones definitivas.
2. Funciona cuando el número de observaciones no es muy grande.
3. No permite comparar claramente diferentes poblaciones

Ejemplo

Como ilustración vamos a crear el gráfico de tallo y hoja para la variable altura (cm) de un grupo de estudiantes de la universidad. Primero se leerán los datos disponibles en github y luego se usará la función stem para obtener el gráfico. A continuación el código usado.

url <- 'https://tinyurl.com/k55nnlu'
datos <- read.table(file=url, header=T)
stem(datos$altura)

## 
##   The decimal point is 1 digit(s) to the right of the |
## 
##   14 | 7
##   15 | 3
##   15 | 679
##   16 | 0001
##   16 | 68888
##   17 | 001334
##   17 | 5678899
##   18 | 000033
##   18 | 88
##   19 | 1

De este gráfico sencillo se puede ver que la variable presenta una mayor frecuencia para alturas ente 170 y 179 cm y que no tiene una distribución simétrica.

2.2 Función boxplot

La función boxplot sirve para crear un diagrama de cajas y bigote para una variable cuantitativa. La estructura de la función boxplot con los argumentos más comunes de uso se muestran a continuación.

boxplot(x, formula, data, subset, na.action,
        range, width, varwidth, notch, names, 
        plot, col, log, horizontal, add, ...)

Los argumentos de la función boxplot son:

• x: vector numérico con los datos para crear el boxplot.
• formula: fórmula con la estructura x ~ g para indicar que las observaciones en el vector x van a ser agrupadas de acuerdo a los niveles del factor g.
• data: marco de datos con las variables.
• subset: un vector opcional para especificar un subconjunto de observaciones a ser usadas en el proceso de ajuste.
• na.action: una función la cual indica lo que debería pasar cuando los datos contienen ``NA’s’’.
• range: valor numérico que indica la extensión de los bigotes. Si es positivo, los bigotes se extenderán hasta el punto más extremo de tal manera que el bigote no supere veces el rango intercuatílico (\(IQ\)). Un valor de cero hace que los bigotes se extiendan hasta los datos extremos.
• width: un vector con los anchos relativos de las cajas.
• varwidth: Si es TRUE, las cajas son dibujadas con anchos proporcionales a las raíces cuadradas del número de observaciones en los grupos.
• notch: si es TRUE, una cuña es dibujada a cada lado de las cajas. Cuando las cuñas de dos gráficos de caja no se traslapan, entonces las medianas son significativamente diferentes a un nivel del 5%.
• names: un con las etiquetas a ser impresas debajo de cada boxplot.
• plot: si es TRUE (por defecto) entonces se produce el gráfico, de lo contrario, se producen los resúmenes de los boxplots.
• col: vector con los colores a usar en el cuerpo de las cajas.
• log: para indicar si las coordenadas x o y o serán graficadas en escala logarítmica.
• ...: otros parámetros gráficos que pueden ser pasados como argumentos para el boxplot.

Ejemplo

Como ilustración vamos a crear dos boxplot para la variable altura (cm) de un grupo de estudiantes de la universidad, el primer boxplot será vertical y el segundo horizontal. Primero se leerán los datos disponibles en github y luego se usará la función boxplot para obtener ambos gráfico. A continuación el código usado.

url <- 'https://tinyurl.com/k55nnlu'
datos <- read.table(file=url, header=T)

par(mfrow=c(1, 2))
boxplot(x=datos$altura, ylab='Altura (cm)')
boxplot(x=datos$altura, xlab='Altura (cm)', horizontal=TRUE)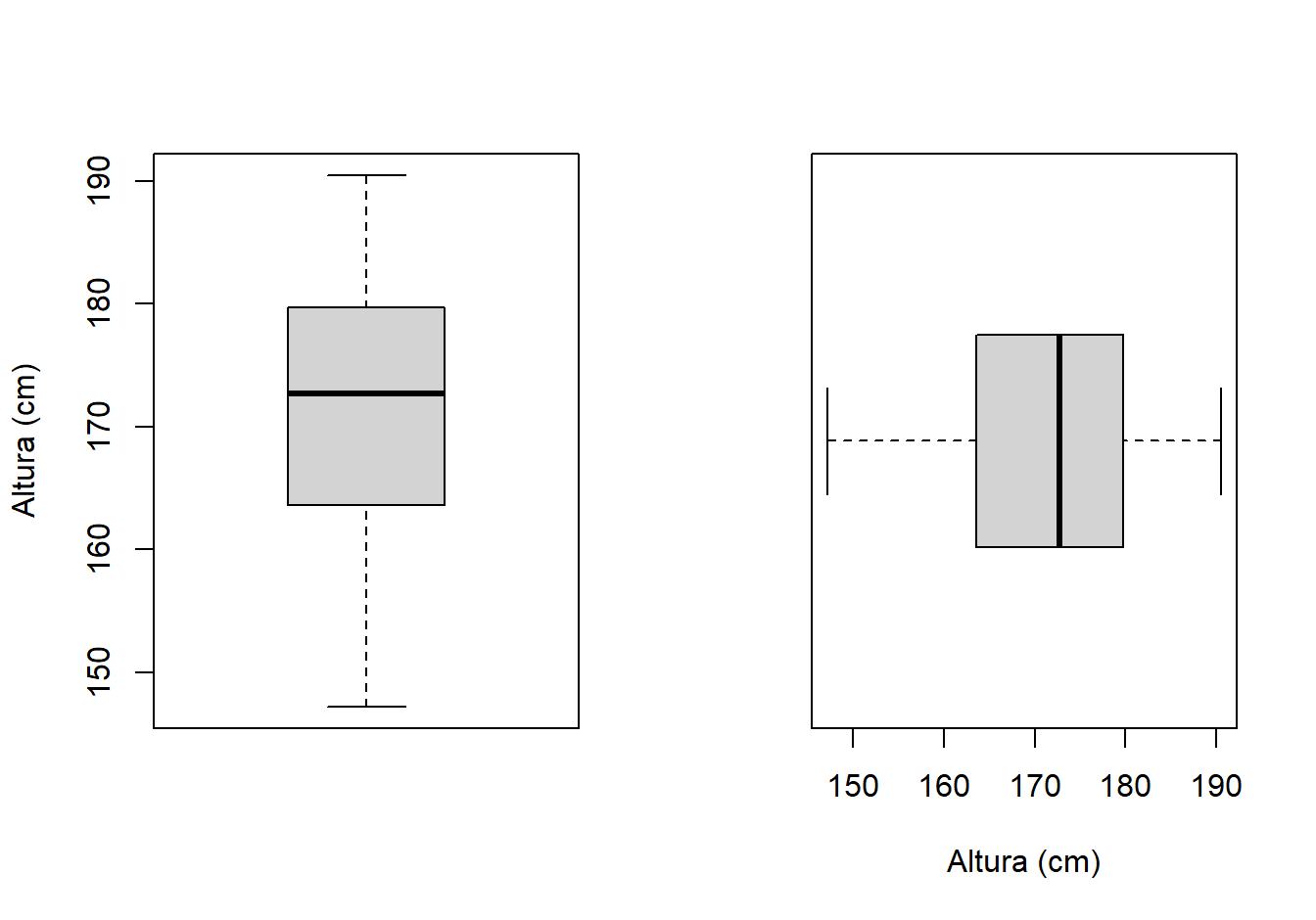

Figure 2.1: Boxplot para la variable altura.

En la Figura 2.1 se presentan los boxplots obtenidos con las instrucciones anteriores. El segundo y tercer boxplot son el mismo, lo único que se modificó fueron los nombres o etiquetas a colocar debajo de cada boxplot por medio del argumento names y la orientación.

Ejemplo

Es posible crear boxplots comparativos usando 1 o 2 variables cualitativas. A continuación se construyen dos boxplots para la variable precio de apartamentos usados en Medellín. En el primer boxtplot diferencia por la variable balcón (no, si) y en el segundo se diferencia por los cruces de las variables parqueadero y ubicación (en Laureles y Poblado).

A continuación se muestra el código necesario para construir los boxplots. En el primero se usa la fórmula precio ~ balcon para crear el boxplot del precio diferenciando por los dos niveles de la variable balcón. En el segundo se usa la fórmula precio ~ ubicacion * parqueadero pero se limitan las ubicaciones a sólo dos, Laureles y Aburrá sur, por esa razón se usa el parámetro subset para incluir la restricción. Se agregó también drop=TRUE para que en el segundo boxplot no aparezcan las otras ubicaciones.

url <- 'https://tinyurl.com/hwhb769'
datos <- read.table(url, header=T)

par(mfrow=c(1, 2))
boxplot(precio ~ balcon, data=datos,
        col=c('lightblue', 'pink'),
        xlab='¿Tiene balcón?', main='(a)',
        ylab='Precio (millones $)')

boxplot(precio ~ ubicacion * parqueadero,
        data=datos, drop=TRUE, col=c('lightblue', 'pink'),
        subset=ubicacion %in% c('laureles', 'aburra sur'),
        xlab='Ubicación y parqueadero',
        ylab='Precio (millones $)', main='(b)')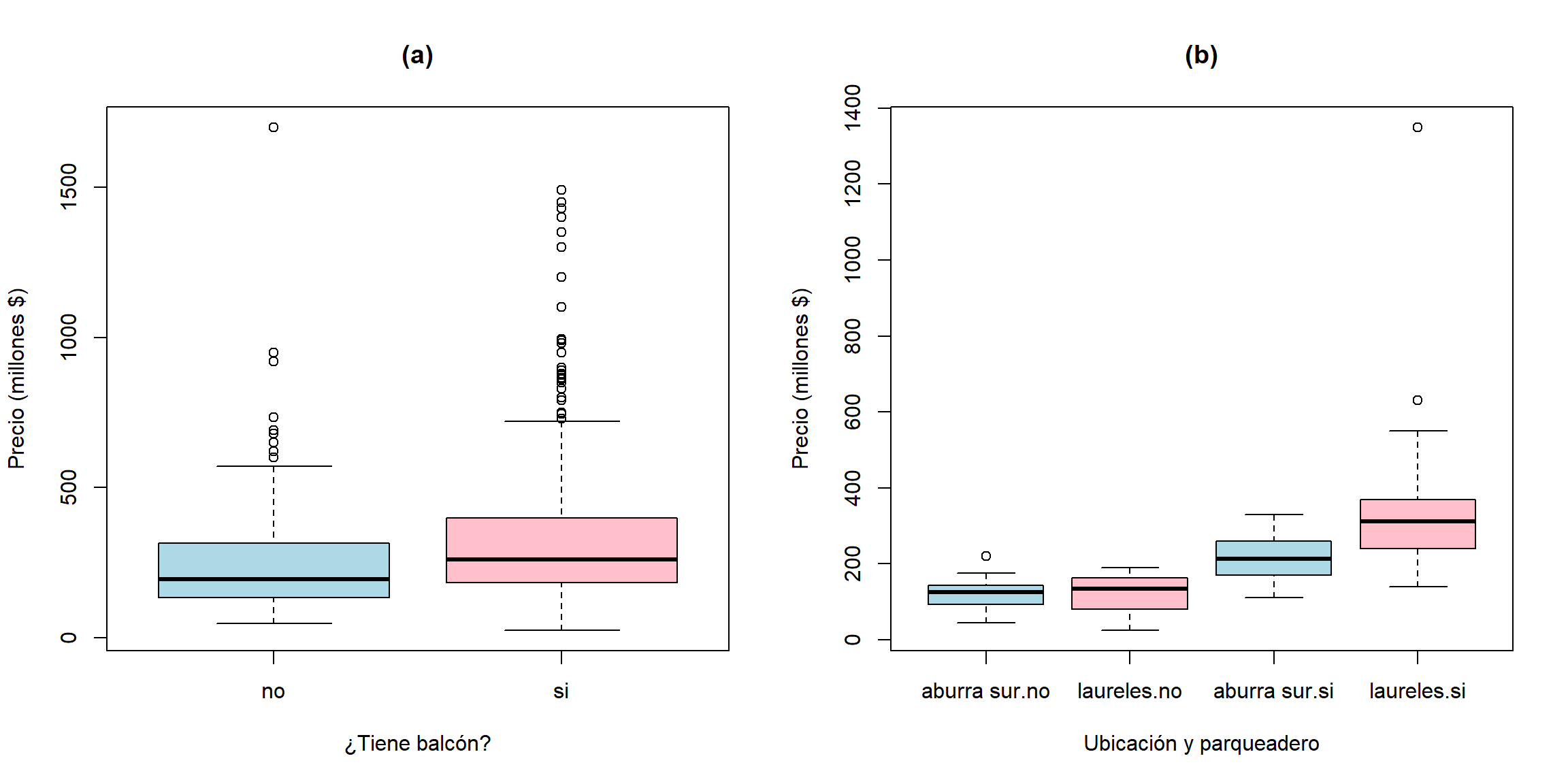

Figure 2.2: Boxplot para la variable precio del apartamento. En el pánel (a) de condiciona por la variable balcón y en el pánel (b) por las combinaciones de las variables ubicación y parqueadero.

En la Figura 2.2 se muestran los boxplots. Se le recomienda al lector construir nuevamente el segundo boxplot pero eliminando drop=TRUE para que vea el efecto que tiene sobre el dibujo.

2.3 Función hist

La función hist sirve para crear el histograma a una variable cuantitativa. Como argumentos esta función recibe un vector con los datos y opcionalmente puede ingresarse como argumento adicional el número de intervalos a ser graficados o en su defecto el número de intervalos se determina con la fórmula de Sturges.

Los programas de computador usualmente construyen los histogramas automáticamente, sin embargo, un buen programa debe permitirnos elegir el número de intervalos del histograma. Si usted posee un programa que no le permite hacer cambios, cambie de programa.

La estructura de la función hist con los argumentos más comunes de uso se muestran a continuación.

• x: vector numérico de valores para construir el histograma.
• breaks: puede ser un número entero que indica el número aproximado de clases o un vector cuyos elementos indican los límites de los intervalos.
• freq: argumento lógico; si se especifica como TRUE, el histograma presentará frecuencias absolutas o conteo de datos para cada intervalo; si se especifica como FALSE el histograma presentar las frecuencias relativas (en porcentaje). Por defecto, este argumento toma el valor de TRUE siempre y cuando los intervalos sean de igual ancho.
• include.lowest: argumento lógico; si se especifica como TRUE, un x[i] igual a los equal a un valor breaks se incluirá en la primera barra, si el argumento right = TRUE, o en la última en caso contrario.
• right: argumento lógico; si es TRUE, los intervalos son abiertos a la izquierda y cerrados a la derecha \((a,b]\). Para la primera clase o intervalo si include.lowest=TRUE el valor más pequeño de los datos será incluido en éste. Si es FALSE los intervalos serán de la forma \([a,b)\) y el argumento include.lowest=TRUE tendrá el significado de incluir el ``más alto’’.
• col: para definir el color de las barras. Por defecto, NULL produce barras sin fondo.
• border: para definir el color de los bordes de las barras.
• plot: argumento lógico. Por defecto es TRUE, y el resultado es el gráfico del histograma; si se especifica como FALSE el resultado es una lista de conteos por cada intervalo.
• labels: argumento lógico o carácter. Si se especifica como TRUE coloca etiquetas arriba de cada barra.
• ...: parámetros gráficos adicionales a title y axis.

Ejemplo

Vamos a construir varios histogramas para los tiempos de 180 corredores de la media maratón de CONAVI realizada hace algunos años. A continuación se muestra la forma de ingresar los 180 datos.

maraton <- c(
10253, 10302, 10307, 10309, 10349, 10353, 10409, 10442, 10447, 
10452, 10504, 10517, 10530, 10540, 10549, 10549, 10606, 10612, 
10646, 10648, 10655, 10707, 10726, 10731, 10737, 10743, 10808, 
10833, 10843, 10920, 10938, 10949, 10954, 10956, 10958, 11004, 
11009, 11024, 11037, 11045, 11046, 11049, 11104, 11127, 11205, 
11207, 11215, 11226, 11233, 11239, 11307, 11330, 11342, 11351, 
11405, 11413, 11438, 11453, 11500, 11501, 11502, 11503, 11527, 
11544, 11549, 11559, 11612, 11617, 11635, 11655, 11731, 11735,
11746, 11800, 11814, 11828, 11832, 11841, 11909, 11926, 11937, 
11940, 11947, 11952, 12005, 12044, 12113, 12209, 12230, 12258, 
12309, 12327, 12341, 12413, 12433, 12440, 12447, 12530, 12600, 
12617, 12640, 12700, 12706, 12727, 12840, 12851, 12851, 12937,
13019, 13040, 13110, 13114, 13122, 13155, 13205, 13210, 13220, 
13228, 13307, 13316, 13335, 13420, 13425, 13435, 13435, 13448, 
13456, 13536, 13608, 13612, 13620, 13646, 13705, 13730, 13730, 
13730, 13747, 13810, 13850, 13854, 13901, 13905, 13907, 13912,
13920, 14000, 14010, 14025, 14152, 14208, 14230, 14344, 14400, 
14455, 14509, 14552, 14652, 15009, 15026, 15242, 15406, 15409, 
15528, 15549, 15644, 15758, 15837, 15916, 15926, 15948, 20055, 
20416, 20520, 20600, 20732, 20748, 20916, 21149, 21714, 23256)

Los datos están codificados como por seis números en el formato hmmss, donde h corresponde a las horas, mm a los minutos y ss a los segundos necesarios para completar la maratón. Antes de construir los histogramas es necesario convertir los tiempos anteriores almacenados en maraton a horas, para esto se utiliza el siguiente código.

horas <- maraton %/% 10000
min <- (maraton - horas * 10000) %/% 100
seg <- maraton - horas * 10000 - min * 100
Tiempos <- horas + min / 60 + seg / 3600

A continuación se muestra el código para construir cuatro histogramas con 2, 4, 8 y 16 intervalos para los tiempos a partir de la variable Tiempos.

par(mfrow=c(2,2))

hist(x=Tiempos, breaks=2, main="", xlab="Tiempo (horas)",
     ylab="Frecuencias", las=1)
mtext("(A)", side=1, line=4, font=1)

hist(x=Tiempos, breaks=4, main="", xlab="Tiempo (horas)",
     ylab="Frecuencias", las=1)
mtext("(B)", side=1, line=4, font=1)

hist(x=Tiempos, breaks=8, main="", xlab="Tiempo (horas)",
     ylab="Frecuencias")
mtext("(C)", side=1, line=4, font=1)

hist(x=Tiempos, breaks=16, main="", xlab="Tiempo (horas)",
     ylab="Frecuencias")
mtext("(D)", side=1, line=4, font=1)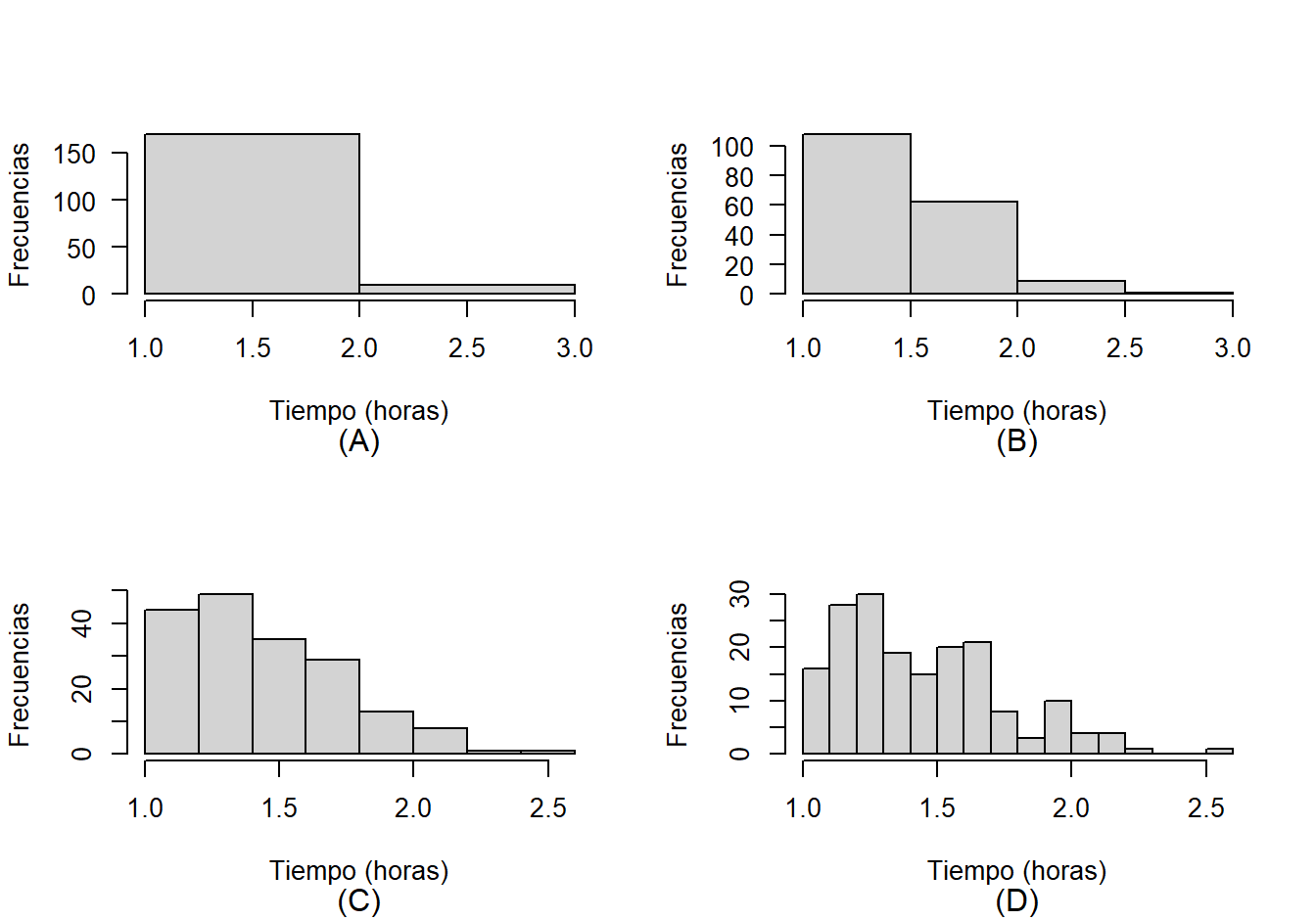

Figure 2.3: Histogramas para el tiempo en la media maratón de CONAVI. A: histograma con dos intervalos, B: histograma con cuatro intervalos, C: histograma con seis intervalos, C: histograma con 18 intervalos.

En la Figura 2.3 se presentan los cuatro histogramas. El histograma C, con 8 barras, muestra más claramente la asimetría (este es el que la mayoría de los programas produce por defecto, ya que la regla de Sturges para este conjunto de datos aproxima a 8 barras). Si consideramos más barras por ejemplo 16, como tenemos en D, se refina más la información y empezamos a notar multimodalidad. En el código anterior se incluyó las = 1 para conseguir que los número del eje Y queden escritos de forma horizontal, ver A y B en Figura 2.3.

A continuación vamos a construir cuatro histogramas: el primero con dos intervalos intervalos y puntos de corte dados por el mínimo, la mediana y el máximo; el segundo con tres intervalos y puntos de corte dados por el mínimo, cuartiles 1, 2, 3 y máximo; el cuarto con diez intervalos y puntos de corte dados por los deciles; y el último con veinte intervalos y puntos de corte dados por cuantiles 5, 10, \(\ldots\), 95. En el código mostrado a continuación se presenta la creación de los puntos de corte y los cuatro histogramas.

puntos1 <- c(quantile(Tiempos, probs=c(0, 0.5, 1)))
puntos2 <- c(quantile(Tiempos, probs=c(0, 0.25, 0.5, 0.75, 1)))
puntos3 <- c(quantile(Tiempos, probs=seq(0, 1, by=0.1)))
puntos4 <- c(quantile(Tiempos, probs=seq(0, 1, by=0.05)))

par(mfrow=c(2, 2))
hist(Tiempos, breaks=puntos1, freq=FALSE, ylim=c(0,2), labels=TRUE,
     main="", ylab="Densidad")
mtext("(A)", side=1, line=4, font=1)
hist(Tiempos, breaks=puntos2, freq=FALSE, ylim=c(0,2), labels=TRUE,
     main="", ylab="Densidad")
mtext("(B)", side=1, line=4, font=1)
hist(Tiempos, breaks=puntos3, freq=FALSE, ylim=c(0,2),
     main="", ylab="Densidad")
mtext("(C)", side=1, line=4, font=1)
hist(Tiempos, breaks=puntos4, freq=FALSE, ylim=c(0,2),
     main="", ylab="Densidad")
mtext("(D)", side=1, line=4, font=1)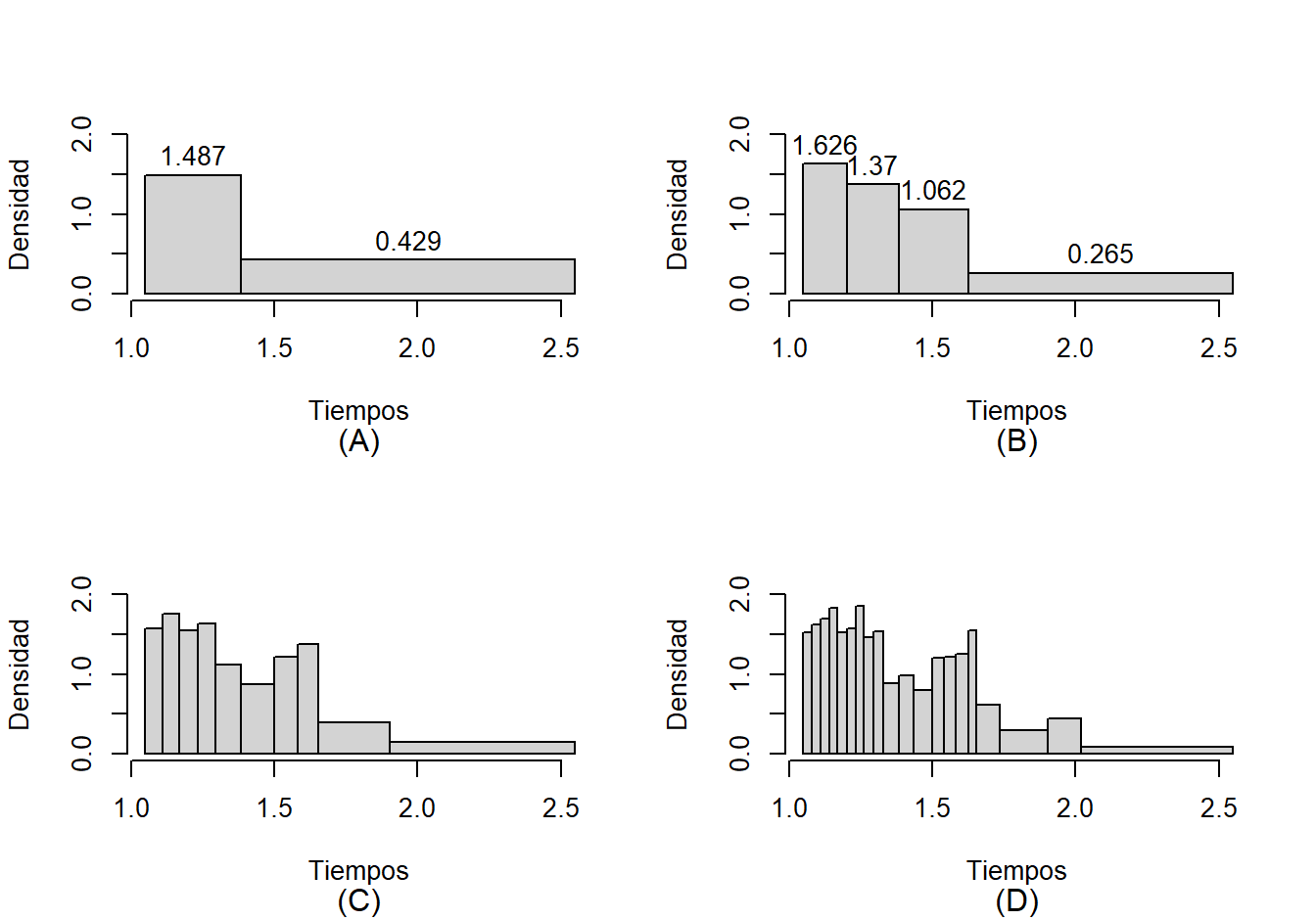

Figure 2.4: Histogramas para el tiempo en la media maratón de CONAVI. A: histograma con dos intervalos, B: histograma con cuatro intervalos, C: histograma con diez intervalos, C: histograma con veinte intervalos.

Nota: En estos histogramas, las alturas corresponden a las intensidades (frec. relativa/long. intervalo). Por tanto, el área de cada rectángulo da cuenta de las frecuencias relativas. Para el caso (A) ambos intervalos tienen igual área y cada uno contiene 50% de los datos. esto puede verificarse así:

Intensidad primera clase = 1.4869888 = 0.5 / (1.384306 - 1.048056)
Intensidad segunda clase = 0.4293381 = 0.5 / (2.548889 - 1.384306)

2.4 Función qqnorm y qqplot

Los gráficos cuantil cuantil (quantile-quantile plot) son una ayuda para explorar si un conjunto de datos o muestra proviene de una población con cierta distribución.

La función qqnorm sirve para explorar la normalidad de una muestra mientras que la función qqplot es de propósito más general, sirve para crear el gráfico cuantil cuantil para cualquier distribución.

La estructura de las funciones con los argumentos más comunes de uso se muestran a continuación.

qqnorm(y, ...)
qqplot(y, x, ...)

La función qqnorm sólo necesita que se le ingrese el vector con la muestra por medio del parámetro y, la función qqplot necesita de la muestra en el parámetro y y que se ingrese en el parámetro x los cuantiles de la población candidata.

Existe otra función útil y es qqline, esta función sirve para agregar una línea de referencia al gráfico cuantil cuantil obtenido con qqnorm.

Ejemplo

Simular 30 observaciones de una distribución \(N(\mu=10, \sigma=4)\) y construir el gráfico cuantil cuantil.

El código para simular la muestra y crear el gráfico cuantil cuantil se muestra a continuación.

muestra <- rnorm(n=30, mean=10, sd=4)

par(mfrow=c(1, 2))
qqnorm(y=muestra)
qqline(y=muestra)

qqnorm(y=muestra, main='', ylab='Cuantiles muestrales',
       xlab='Cuantiles teóricos', las=1)
qqline(y=muestra, col='blue', lwd=2, lty=2)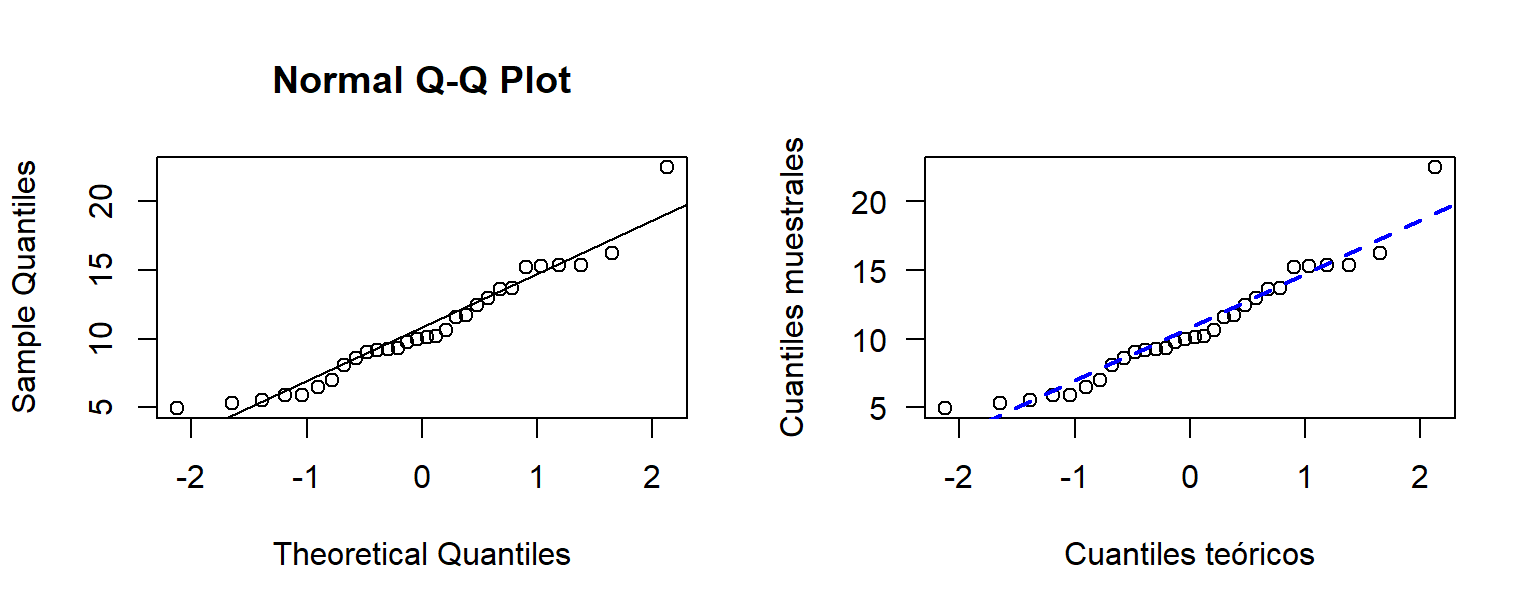

Figure 2.5: Gráfico cuantil cuantil para una muestra generada de una población normal.

En la izquierda de la Figura 2.5 está el gráfico cuantil cuantil sin editar, en la derecha se encuentra el gráfico luego de modificar los nombres de los ejes, grosor y color de la línea de referencia.

Ejemplo

Simular 100 observaciones de una distribución \(Weibull(1,1)\) y construir dos gráficos cuantil cuantil, el primero tomando como referencia los cuantiles de una \(N(0,1)\) y el segundo tomando los cuantiles de la \(Weibull(1,1)\).

El código para simular la muestra y crear los gráficos cuantil cuantil se muestra a continuación.

n <- 100
muestra <- rweibull(n=n, shape=1, scale=1)

par(mfrow=c(1, 2))
qqplot(y=muestra, x=qnorm(ppoints(n)))
qqplot(y=muestra, x=qweibull(ppoints(n), shape=1, scale=1))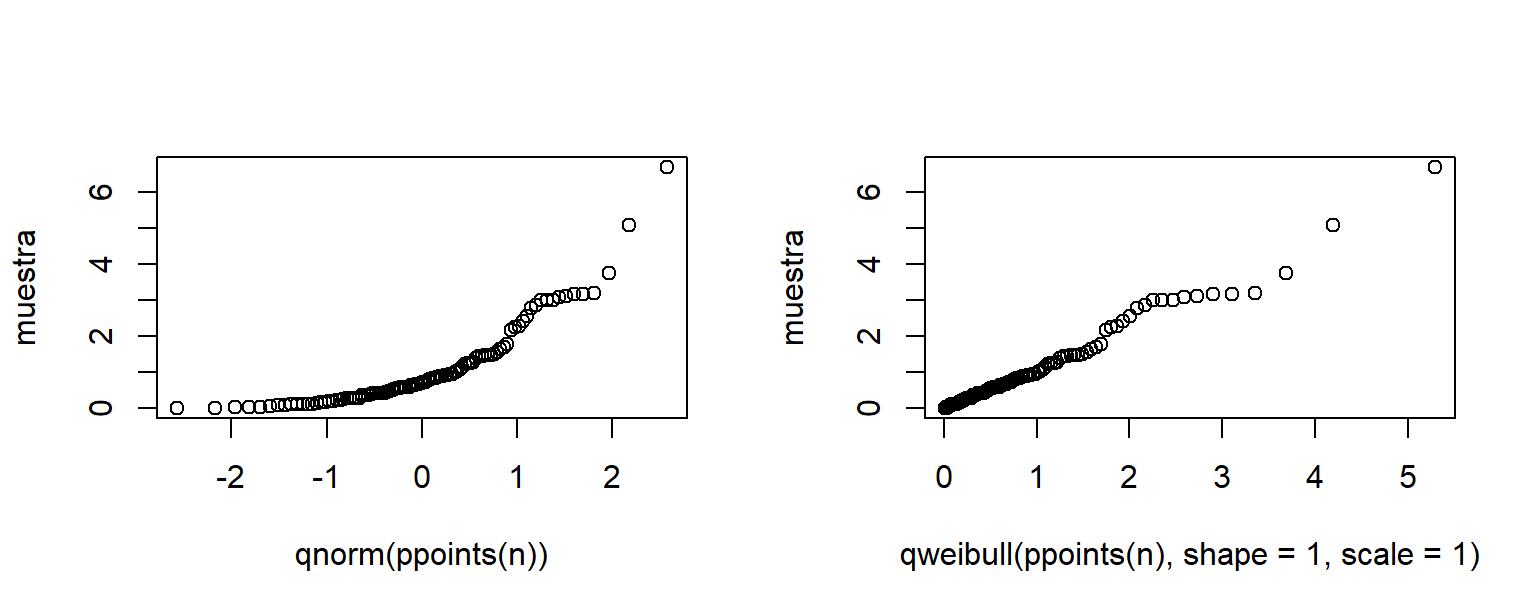

Figure 2.6: Gráfico cuantil cuantil para una muestra generada de una población Weibull.

En la Figura 2.6 están los gráficos cuantil cuantil solicitados. Del pánel izquierdo de la figura vemos que los puntos NO están alineados, esto indica que la muestra no proviene de la distribución \(N(0, 1)\), esto es un resultado esperado ya que sabíamos que la muestra no fue generada de una normal. En el pánel derecho de la misma figura vemos que los puntos SI están alineados, esto indica que la muestra generada puede provenir de una población \(Weibull(1, 1)\). Los nombres de los ejes en la Figura 2.6 pueden ser editados para presentar una figura con mejor apariencia.

2.5 Función density

Los gráficos de densidad son muy útiles porque permiten ver el(los) intervalo(s) donde una variable cuantitativa puede ocurrir con mayor probabilidad.

La función density crea la información de la densidad y la función plot dibuja la densidad.

La estructura de la función density con los argumentos más comunes de uso se muestra a continuación.

density(x, bw, adjust=1, kernel='gaussian', na.rm=FALSE)

Los argumentos de la función density son:

• x: vector con los datos para los cuales se quiere la densidad.
• bw: ancho de banda.
• kernel: núcleo de suavización a usar, los posibles valores son gaussian, rectangular, triangular, epanechnikov, biweight, cosine o optcosine, el valor por defecto es gaussian.
• na.rm: valor lógico, si es TRUE se eliminan los valores con NA para construir la densidad, el valor por defecto es FALSE.

Ejemplo

Simular mil observaciones de una \(N(0, 1)\), aplicar la función density al vector y explorar el contenido de la salida.

Primero se generan las observaciones y se almacenan en el objeto y, luego se aplica la función density y el resultado se guarda en el objeto res, para explorar lo que almacena res se usa la función names. A continuación el código utilizado.

y <- rnorm(n=1000)
res <- density(y)
names(res)

## [1] "x"         "y"         "bw"        "n"         "call"      "data.name"
## [7] "has.na"

De la salida anterior se observa que la lista res tiene 7 elementos, los dos primeros son los vectores con las coordenadas para dibujar la densidad, los restantes elementos con información adicional.

Ejemplo

Con los datos generados en el ejemplo anterior construir la densidad para varios núcleo y para varios valores de ancho de banda.

En el siguiente código se construyen 4 densidades para diferentes núcleos.

par(mfrow=c(2, 2))
plot(density(y, kernel='gaussian'))
plot(density(y, kernel='triangular'))
plot(density(y, kernel='cosine'))
plot(density(y, kernel='rectangular'))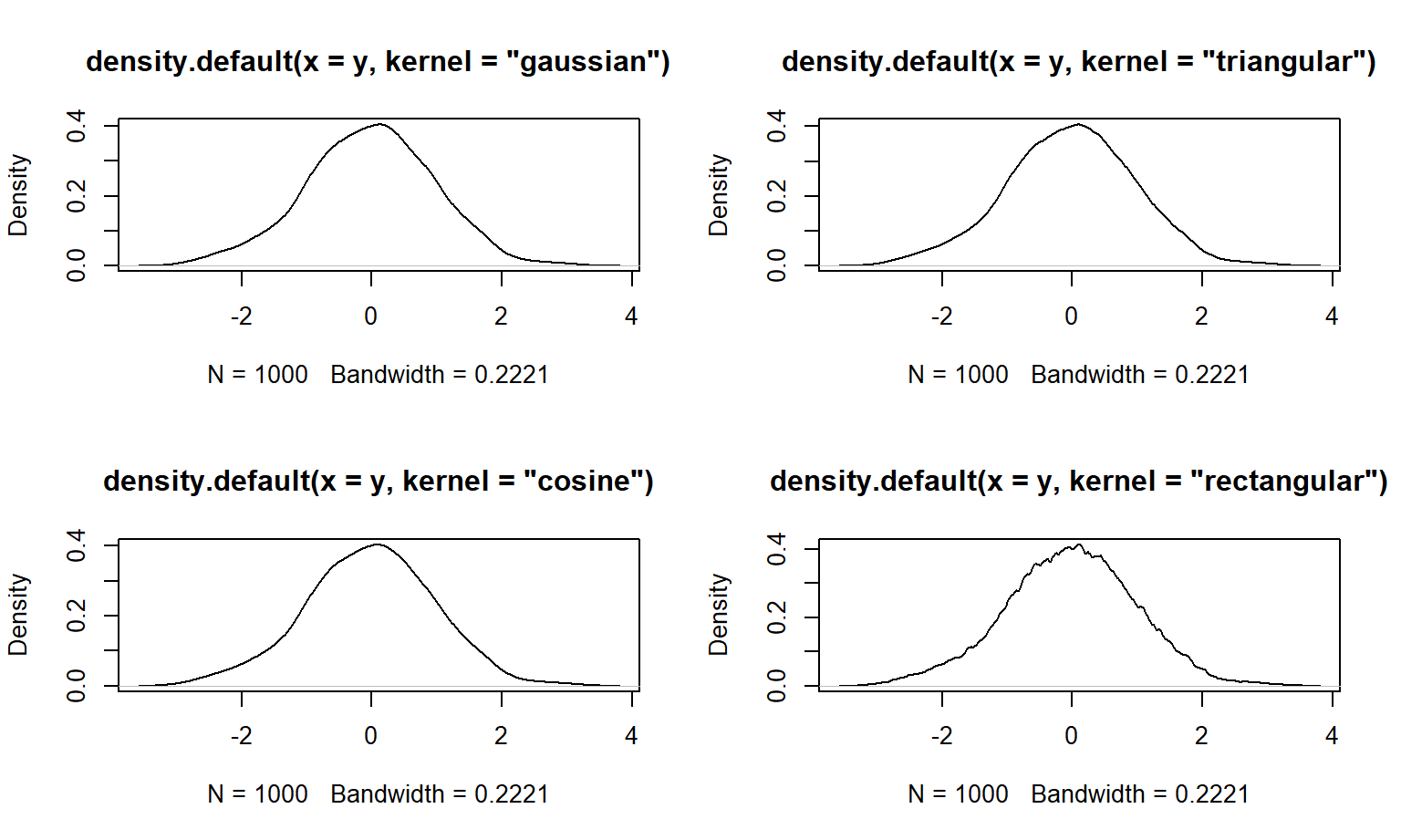

Figure 2.7: Densidad para una muestra aleatoria de una N(0, 1) cambiando el núcleo de la densidad.

En la Figura 2.7 se muestran las densidades para 4 elecciones del núcleo. En la práctica se usa el núcleo que está por defecto (gaussian) ya que el objetivo de una densidad es ver la zonas donde es más probable encontrar observaciones de la variable.

En el siguiente código se construyen 4 densidades para diferentes anchos de banda.

par(mfrow=c(2, 2))
plot(density(y, bw=0.1))
plot(density(y, bw=0.2241))  # bw obtenido antes
plot(density(y, bw=0.5))
plot(density(y, bw=1))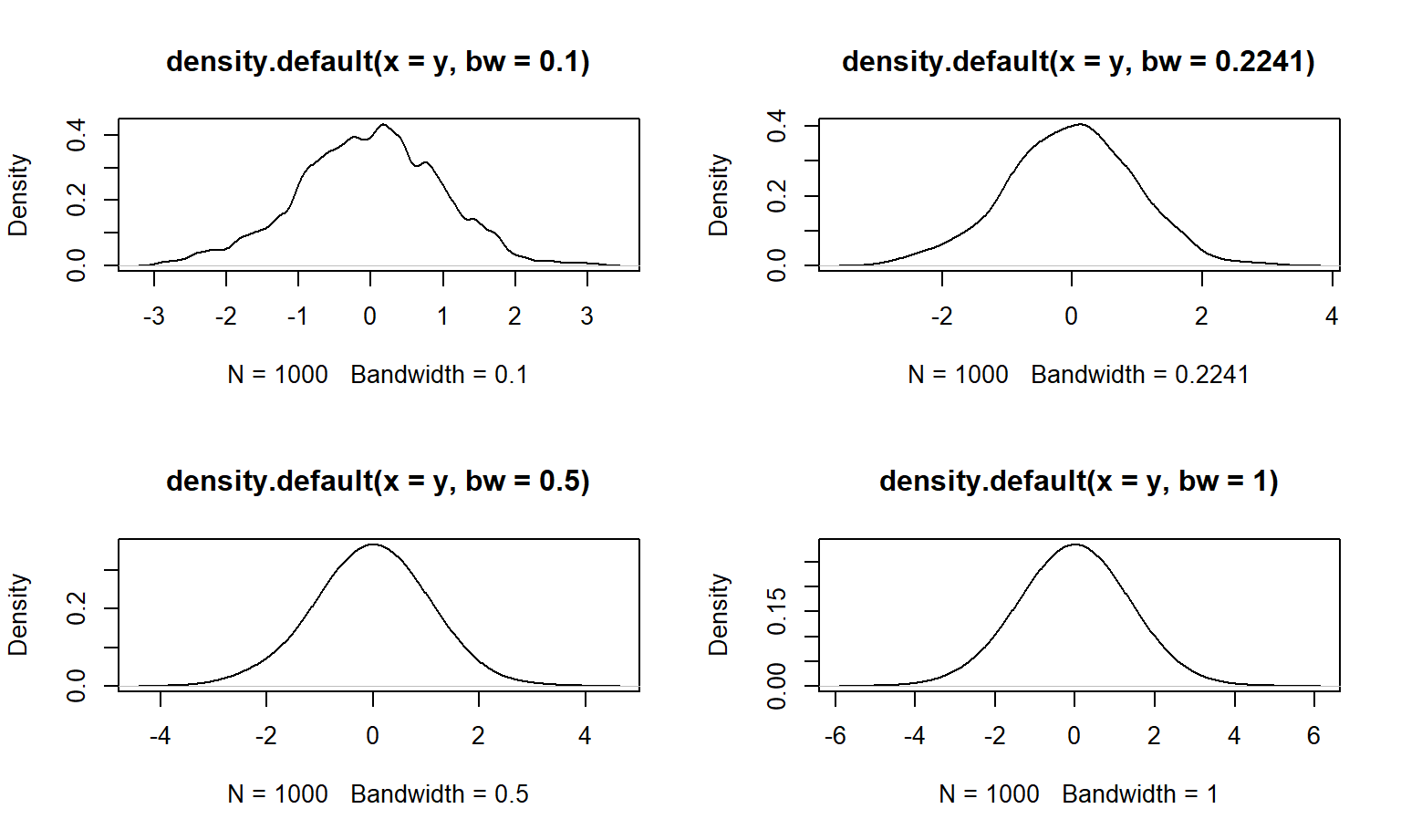

Figure 2.8: Densidad para una muestra aleatoria de una N(0, 1) cambiando el ancho de banda.

En la Figura 2.8 se muestran las densidades para 4 elecciones del parámetro ancho de banda bw, el valor de 0.2241 fue el valor calculado automáticamente por R y fue obtenido de la Figura 2.7, los otros valores fueron elegidos arbitrariamente para ver los cambios en la densidad. El usar un ancho de banda pequeño la densidad queda muy rugosa y usar un valor muy grande la suaviza, se recomienda usar el valor automático.

Ejemplo

Construir un gráfico de densidad para la variable peso corporal de la base de datos medidas_cuerpo, luego construir la densidad para la misma variable pero diferenciando por sexo.

url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)

par(mfrow=c(1, 2))
plot(density(datos$peso), main='Distribución del peso corporal',
     xlab='Peso corporal (kg)', ylab='Densidad', lwd=4)

den.hom <- with(datos, density(peso[sexo == 'Hombre']))
den.muj <- with(datos, density(peso[sexo == 'Mujer']))

plot(den.hom, xlim=c(20, 120), 
     main='Distribución del peso corporal por género', ylab='Densidad',
     xlab='Peso corporal (kg)', lwd=4, col='blue')
lines(den.muj, lwd=4, col='red')
legend('topright', legend=c('Hombres', 'Mujeres'), bty='n',
       lwd=3, col=c('blue', 'red'))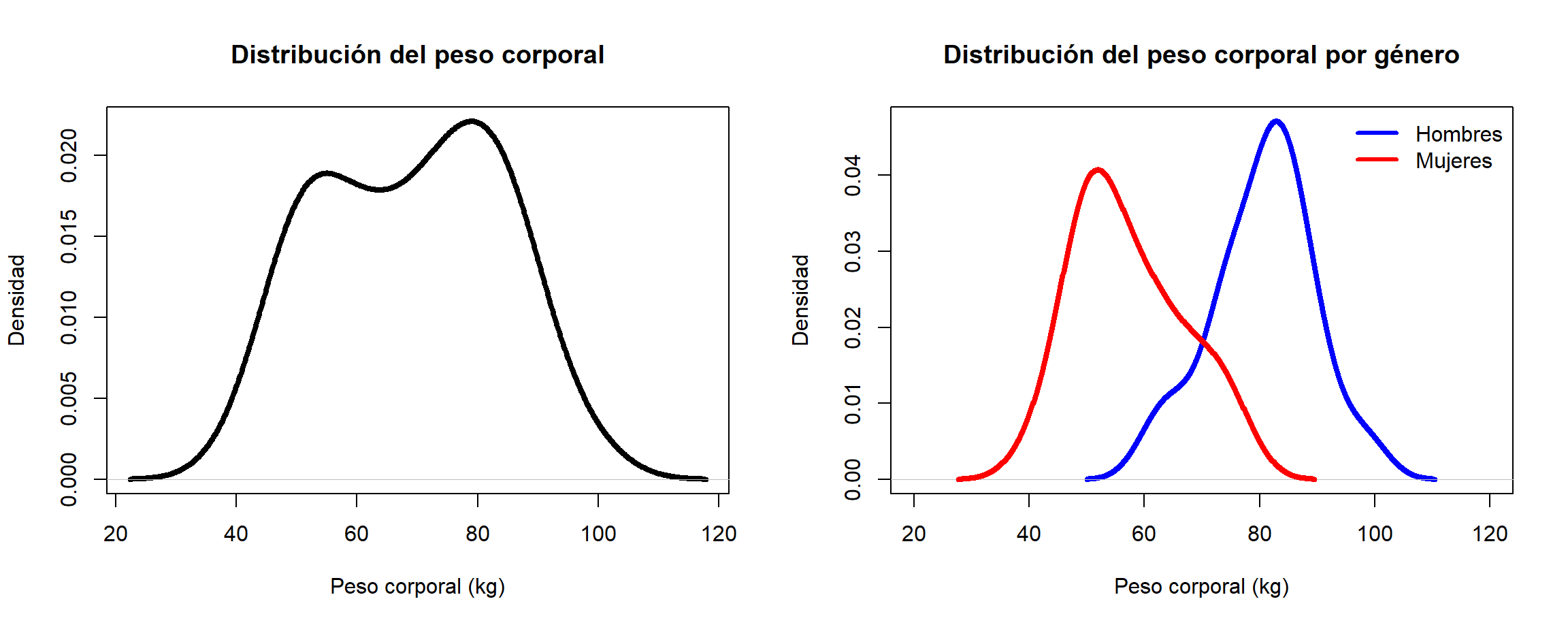

Figure 2.9: Densidad para la variable peso en la izquierda, densidad para el peso diferenciando por sexo a la derecha.

En el panel izquierdo de la Figura 2.9 se muestra la densidad para la variable peso, de esta figura se observa que tiene dos sectores de mayor densidad, alrededor de 50 kg y alrededor de 80 kg. En el panel izquierdo están la densidades del peso corporal para hombres y mujeres, aquí se observa claramente la diferencia entre los pesos de hombres y mujeres.