3 Gráficos para varias variables cuantitativas

En este capítulo se presentan funciones para la creación de gráficos que involucran varias variables cuantitativas.

3.1 Función plot

Los gráficos de dispersión son muy útiles porque permiten ver la relación que existe entre dos variables cuantitativas, la función plot permite crear este tipo de gráficos. La estructura de la función plot con los argumentos más usuales se muestra a continuación:

plot(x, y, type, main, sub, xlab, ylab)

Los argumentos de la función plot son:

• x: vector numérico con las coordenadas del eje horizontal.
• y: vector numérico con las coordenadas del eje vertical.
• type: tipo de gráfico a dibujar. Las opciones son: {#par_type}
  • 'p' para obtener puntos, esta es la opción por defecto.
  • 'l' para obtener líneas.
  • 'b' para obtener los puntos y líneas que unen los puntos.
  • 'c' para obtener sólo las líneas y dejando los espacios donde estaban los puntos obtenidos con la opción 'b'.
  • 'o' para obtener los puntos y lineas superpuestas.
  • 'h' para obtener líneas verticales desde el origen hasta el valor \(y_i\) de cada punto, similar a un histograma.
  • 's' para obtener escalones.
  • 'S' similar al anterior.
  • 'n' para que no dibuje.
• ...: otros parámetros gráficos que pueden ser pasados como argumentos para plot.

Ejemplo

Crear 16 parejas de puntos tales que \(x=-5, -4, \ldots, 9, 10\) con \(y=-10+(x-3)^2\), dibujar los nueve diagramas de dispersión de \(y\) contra \(x\) usando todos los valores posibles para el parámetro type.

A continuación se muestra el código para crear las 16 parejas de \(x\) e \(y\). Los nueve diagramas de dispersión se observan en la Figura 3.1, de esta figura se observa claramente el efecto que tiene el parámetro type en la construcción del diagrama de dispersión.

x <- -5:10
y <- -10 + (x-3)^2
par(mfrow=c(3, 3))
plot(x=x, y=y, type='p', main="con type='p'")
plot(x=x, y=y, type='l', main="con type='l'")
plot(x=x, y=y, type='b', main="con type='b'")
plot(x=x, y=y, type='c', main="con type='c'")
plot(x=x, y=y, type='o', main="con type='o'")
plot(x=x, y=y, type='h', main="con type='h'")
plot(x=x, y=y, type='s', main="con type='s'")
plot(x=x, y=y, type='S', main="con type='S'")
plot(x=x, y=y, type='n', main="con type='n'")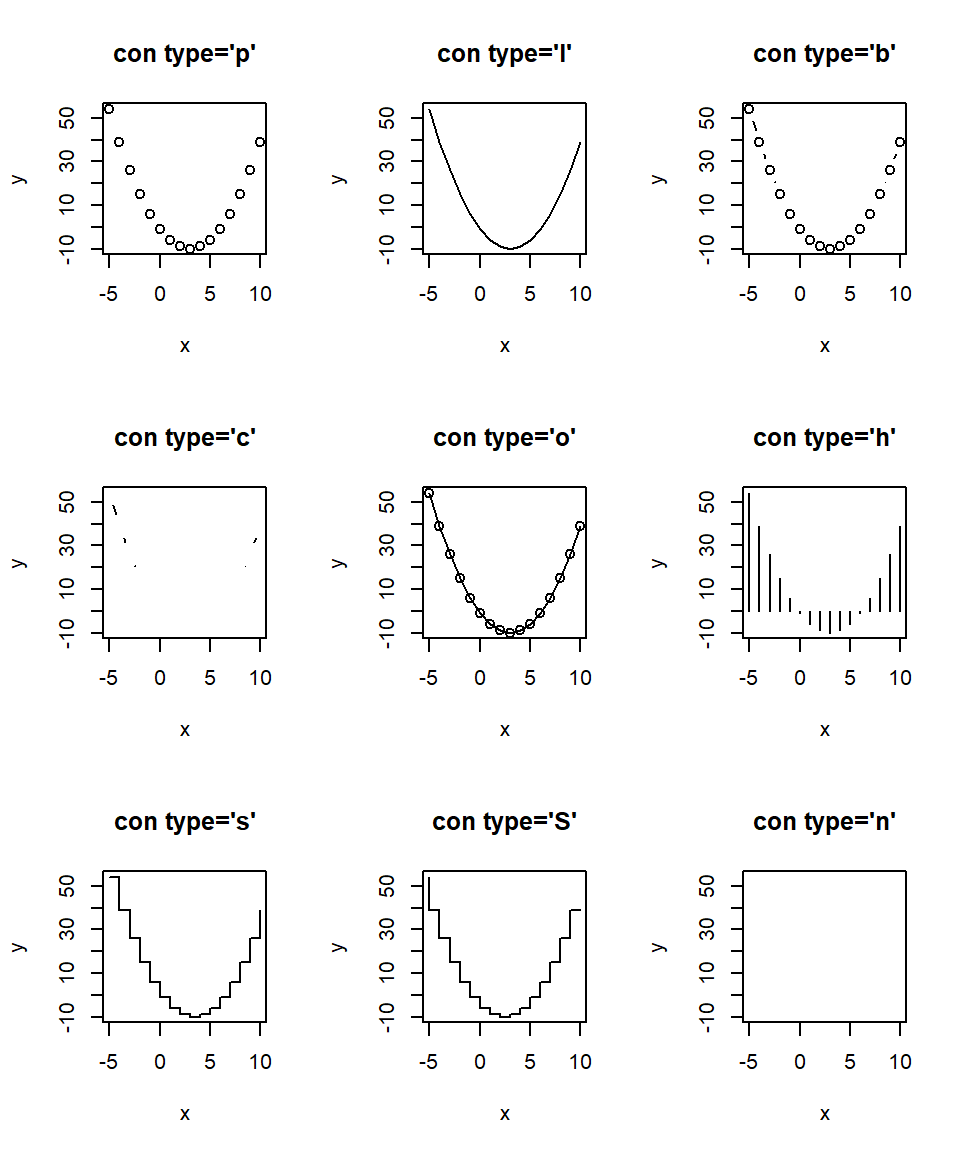

Figure 3.1: Efecto del parámetro type en la función plot.

Ejemplo

Como ilustración vamos a crear dos diagramas de dispersión entre el precio de apartamentos usados en la ciudad de Medellín y el área de los apartamentos. El primer diagrama es un gráfico básico mientras que el segundo es un diagrama mejorado.

El código necesario para cargar la base de datos y construir los diagramas de dispersión se muestra a continuación.

url <- 'https://tinyurl.com/hwhb769'
datos <- read.table(file=url, header=T)

par(mfrow=c(1, 2))
plot(x=datos$mt2, y=datos$precio)
plot(x=datos$mt2, y=datos$precio, pch='.',
     xlab='Área del apartamento (m2)',
     ylab='Precio (millones de pesos)')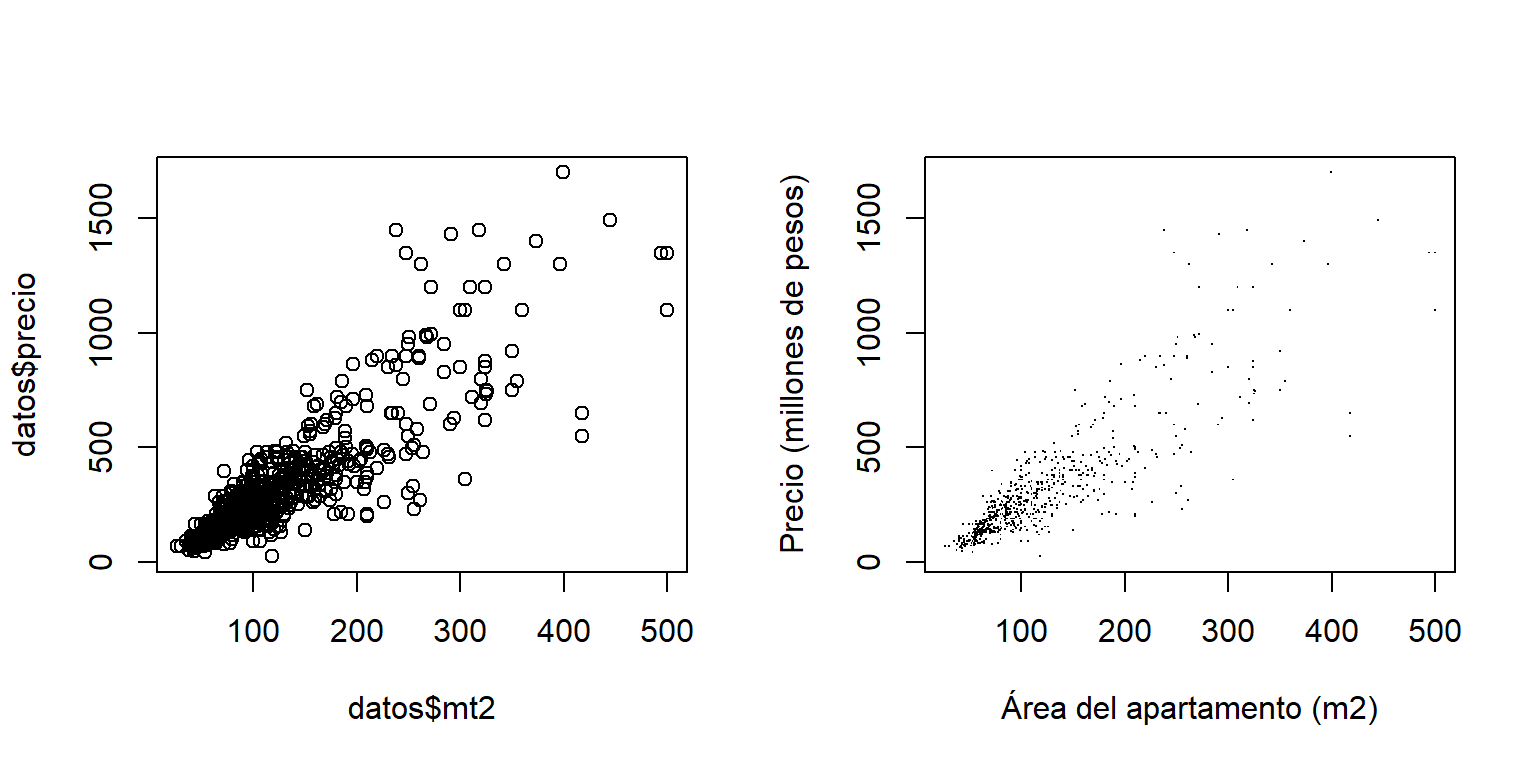

Figure 3.2: Diagrama de dispersión del precio del apartamento versus área del apartamento. A la izquierda el diagrama de dispersión sin editar y a la derecha el diagrama de dispersión mejorado.

En la Figura 3.2 se presentan los diagramas de dispersión entre precio y área de los apartamentos. En el panel de la izquierda está el diagrama básico, de este diagrama se observa claramente que a medida que los apartamentos tienen mayor área el precio promedio y la variabilidad del precio aumentan. En la parte inferior izquierda de este diagrama se tiene una zona de alta densidad de puntos y por esa razón se observa una mancha en el diagrama. Para la construcción del diagrama de dispersión mostrado en el panel derecho se usó el parámetro pch='.' con el objetivo de obtener pequeños puntos que representen cada apartamento y que no se traslapen debido a que se tienen 694 observaciones en la base de datos.

3.2 Función sunflowerplot

La función sunflowerplot sirve para crear gráficos de dispersión en los cuales hay parejas repetidas que se superponen y que por lo tanto no se podrían apreciar.

Si una pareja está una sola vez se representará por un punto; si la pareja se repite dos veces se representará por un punto y dos rayitas rojas (pétalos); si la pareja se repite tres veces se representará por un punto y tres rayitas rojas (pétalos) y así sucesivamente.

La estructura de la función sunflowerplot con los argumentos más usuales se muestra a continuación:

sunflowerplot(x, y, pch, seg.col, seg.lwd, ...)

Los argumentos de la función plot son:

• x: vector numérico con las coordenadas del eje horizontal.

• y: vector numérico con las coordenadas del eje vertical.

• pch: valor o vector numérico con el tipo de punto a usar, por defecto pch=1. Para conocer los diferentes símbolos que se pueden obtener con el parámetro pch se recomienda consultar la Figura 6.11.

• seg.col: color de los pétalos.

• seg.lwd: ancho de los pétalos.

• ...: otros parámetros gráficos que pueden ser pasados como argumentos para plot.

A continuación se presenta un ejemplo en los cuales se usa la función sunflowerplot para crear gráficos de dispersión.

Ejemplo

Suponga que se tiene el punto (1, 1) una sola vez, el punto (2, 3) repetido cuatro veces, el punto (3, 2) repetido seis veces y el punto (4, 5) repetido dos veces. El objetivo es crear dos gráficos de dispersión con los trece puntos, uno con la función plot y el otro con la función sunflowerplot para comparar los resultados.

A continuación se muestra el código con la creación de los vectores y los dos gráficos de dispersión con plot y sunflowerplot.

x <- c(1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4)
y <- c(1, 3, 3, 3, 3, 2, 2, 2, 2, 2, 2, 5, 5)

par(mfrow=c(1, 2))
plot(x, y, main='a) Usando plot')
sunflowerplot(x, y, seg.col='blue', seg.lwd=2, cex=1.5,
              main='b) Usando sunflowerplot')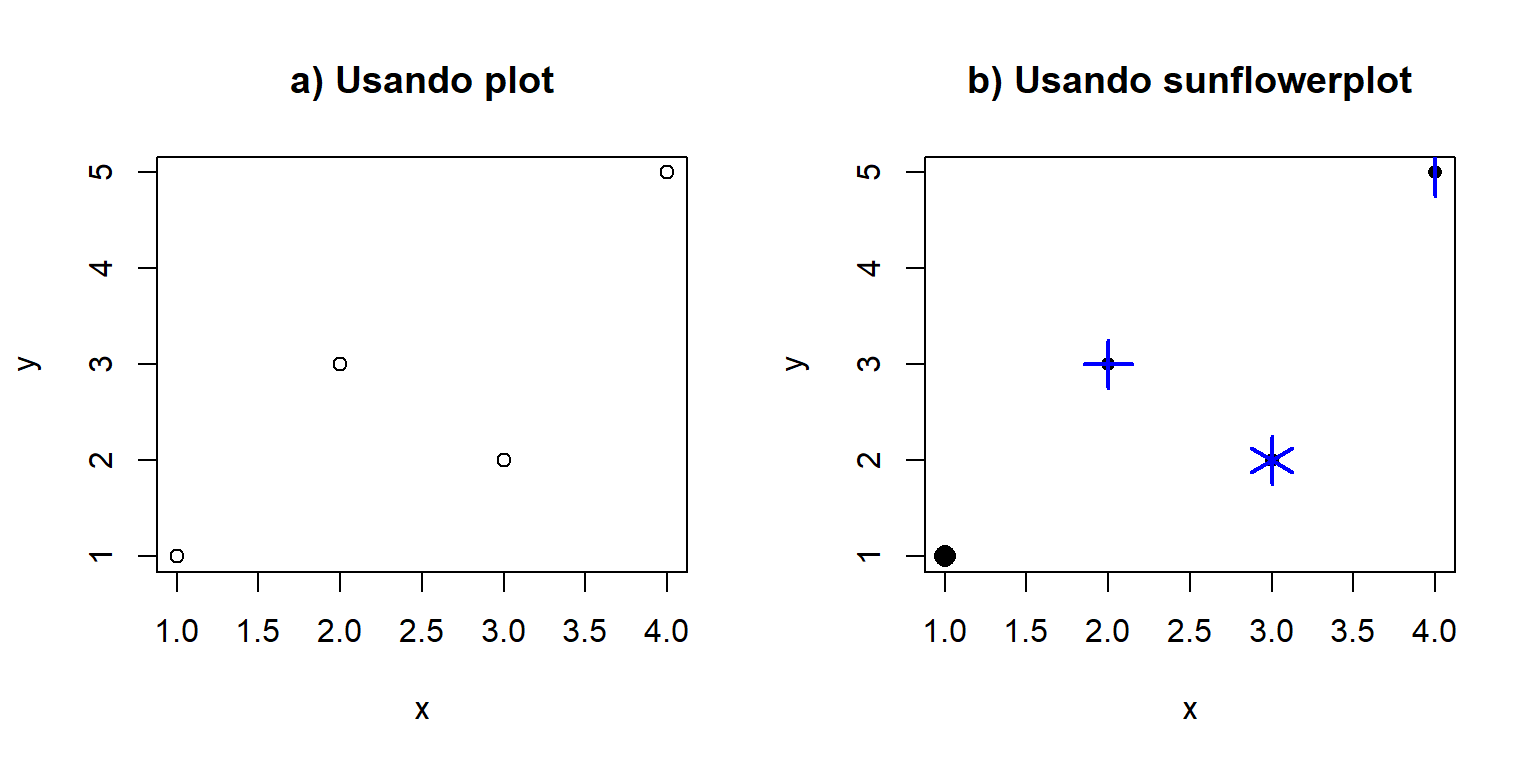

Figure 3.3: Gráfico de dispersión para datos hipotéticos. En la izquierda el gráfico obtenido con plot y a la derecha el obtenido con sunflowerplot.

En la Figura 3.3 se muestran los dos gráficos de dispersión para los datos. En el panel de la izquierda está el diagrama obtenido con la función plot pero sólo se observan 4 puntos cuando en realidad eran 13, esto se debe a que hay puntos repetidos y éstos quedan unos sobre otros. En el panel de la derecha está el diagrama obtenido con la función sunflowerplot, en este diagrama se observan cuatro objetos: el punto con coordenadas (1, 1) se representó con un punto ya que él no se repite, el punto (2, 3) está representado por un punto y cuatro pétalos de color azul ya que él se repite cuatro veces, y los puntos (3, 2) y (4, 5) se represetan con seis y dos pétalos porque esas son las veces que ellos se repiten.

Ejemplo

Como ilustración vamos a crear un diagrama de dispersión con la función sunflowerplot para las variables número de alcobas y número de baños de la base de datos de apartamentos usados.

El código necesario para cargar la base de datos y construir el diagrama de dispersión se muestra a continuación. El diagrama de dispersión se construyó excluyendo la información del apartamento 594 porque éste aparece con 14 alcobas.

url <- 'https://tinyurl.com/hwhb769'
datos <- read.table(file=url, header=T)
datos <- datos[-594, ]  # Sacando el apto 594
sunflowerplot(x=datos$alcobas, y=datos$banos)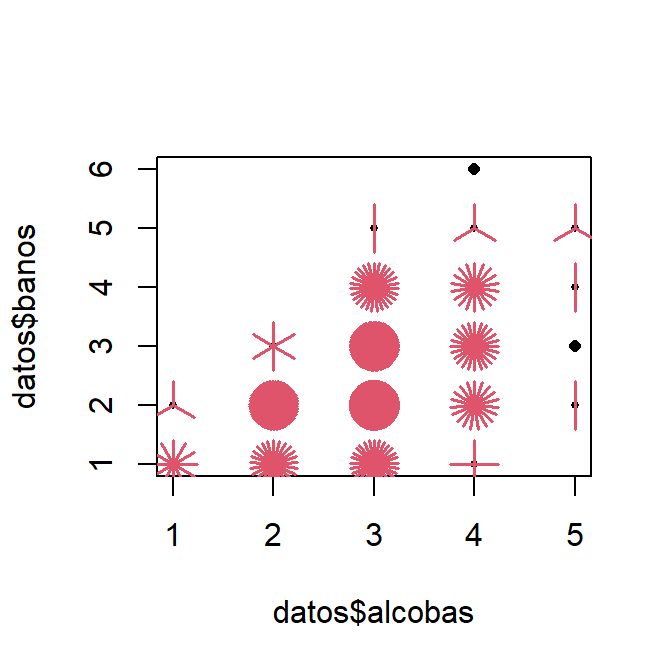

Figure 3.4: Diagrama de dispersión para número de baños versus número de alcobas.

En la Figura 3.4 se muestra el diagrama de dispersión entre número de baños y número de alcobas. De este diagrama se observa que la mayor parte de los apartamentos de la base de datos tienen 2 o 3 alcobas con 2 o 3 baños, se nota que sólo 8 apartamentos tiene 5 alcobas y que sólo un apatamento tiene seis baños.

3.3 Función symbols

La función symbols sirve para construir diagramas de dispersión en dos dimensiones incluyendo información adicional de variables cuantitativas.

Ejemplo

Como ilustración vamos a crear un diagrama de dispersión entre el precio de apartamentos usados en la ciudad de Medellín y el área de los apartamentos pero incluyendo otras variables.

url <- 'https://tinyurl.com/hwhb769'
datos <- read.table(url, header=T)
subdat <- subset(datos, ubicacion == 'centro')

par(mfrow=c(1, 2))
with(subdat, symbols(x=mt2, y=precio,
                     circles=alcobas, 
                     las=1, inches=0.4, 
                     fg='red',
                     main='Radio = N° alcobas'))

with(subdat, symbols(x=mt2, y=precio,
                     squares=alcobas, 
                     las=1, inches=0.4, 
                     fg='dodgerblue4', bg='pink',
                     main='Lado = N° alcobas'))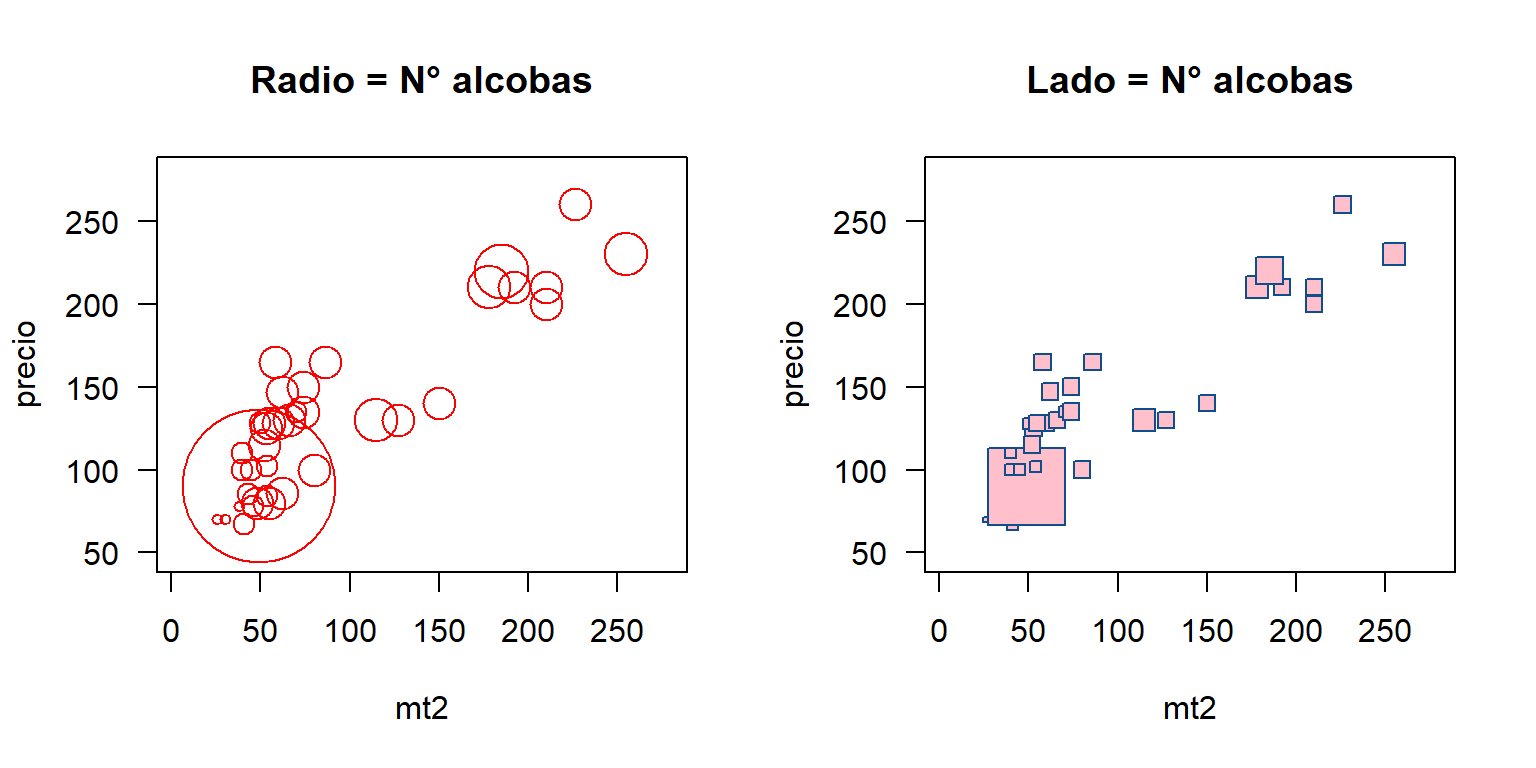

Figure 3.5: Diagrama de dispersión con los símbolos circle y squares para incluir más variables.

par(mfrow=c(1, 2))
with(subdat, symbols(x=mt2, y=precio,
                     rectangles=cbind(estrato, alcobas), 
                     las=1, inches=0.4, 
                     fg='chartreuse4', bg='yellow',
                     main='Ancho = estrato y Alto = N° alcobas'))

with(subdat, symbols(x=mt2, y=precio,
                     stars=cbind(estrato, alcobas,
                                 banos), 
                     las=1, inches=0.4, 
                     fg='purple1', bg='tomato',
                     main='Estrato, alcobas y n° baños'))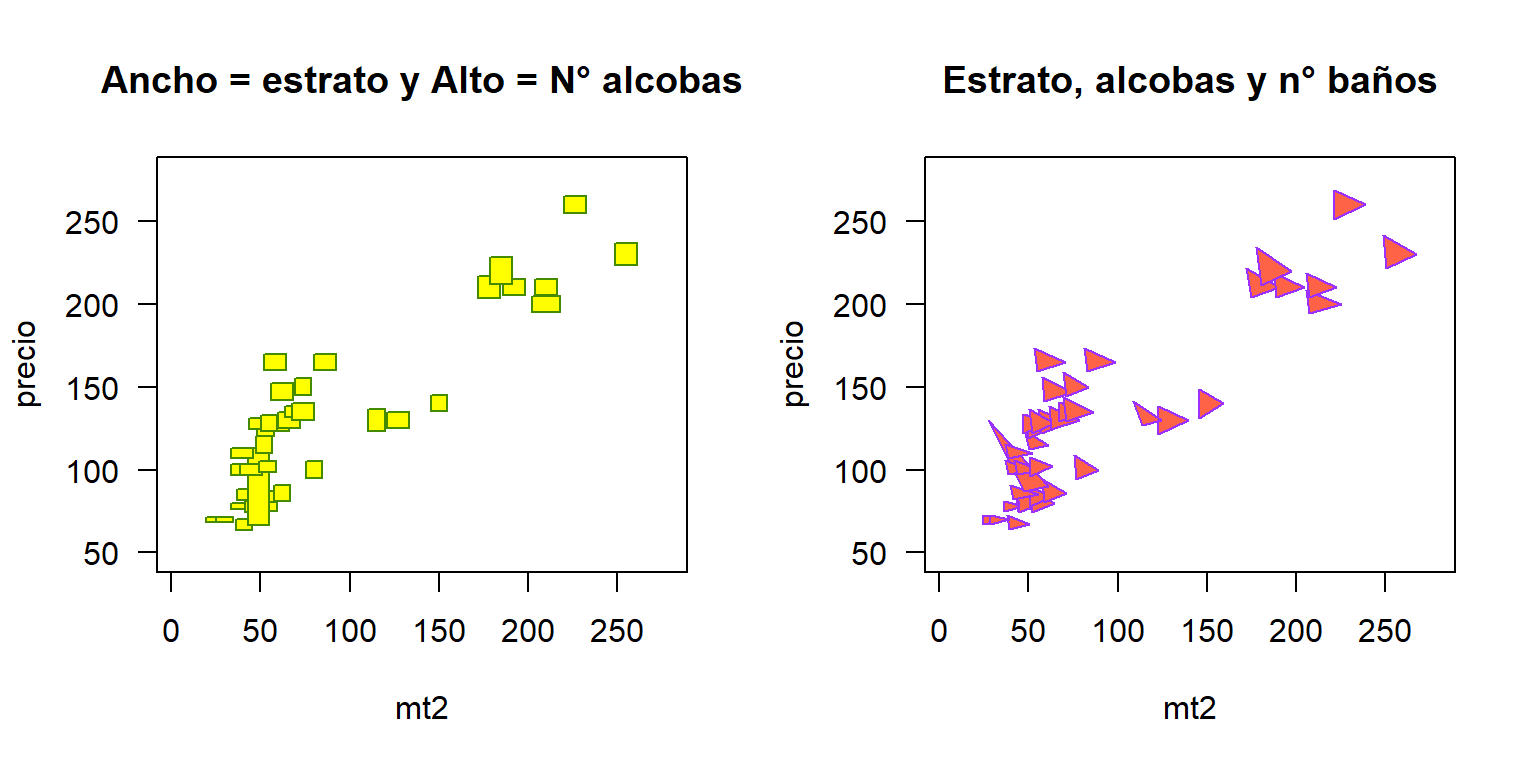

Figure 3.6: Diagrama de dispersión con los símbolos rectangles y stars para incluir más variables.

3.4 Función pairs

Las matrices de dispersión obtenidas con la función pairs proporcionan un método simple de presentar las relaciones entre pares de variables cuantitativas y son la versión múltiple de la función plot. Este gráfico consiste en una matriz donde cada entrada presenta un gráfico de dispersión sencillo. Un inconveniente es que si tenemos muchas variables el tamaño de cada entrada se reduce demasiado impidiendo ver con claridad las relaciones entre los pares de variables. La celda \((i,j)\) de una matriz de dispersión contiene el gráfico de dispersión de la columna \(i\) versus la columna \(j\) de la matriz de datos.

En la Figura 3.7 se muestra un ejemplo de una matriz de dispersión para un conjunto de datos, en la diagonal están los nombres de las variables y por fuera de la diagonal están los diagramas de dispersión para cada combinación de variables.

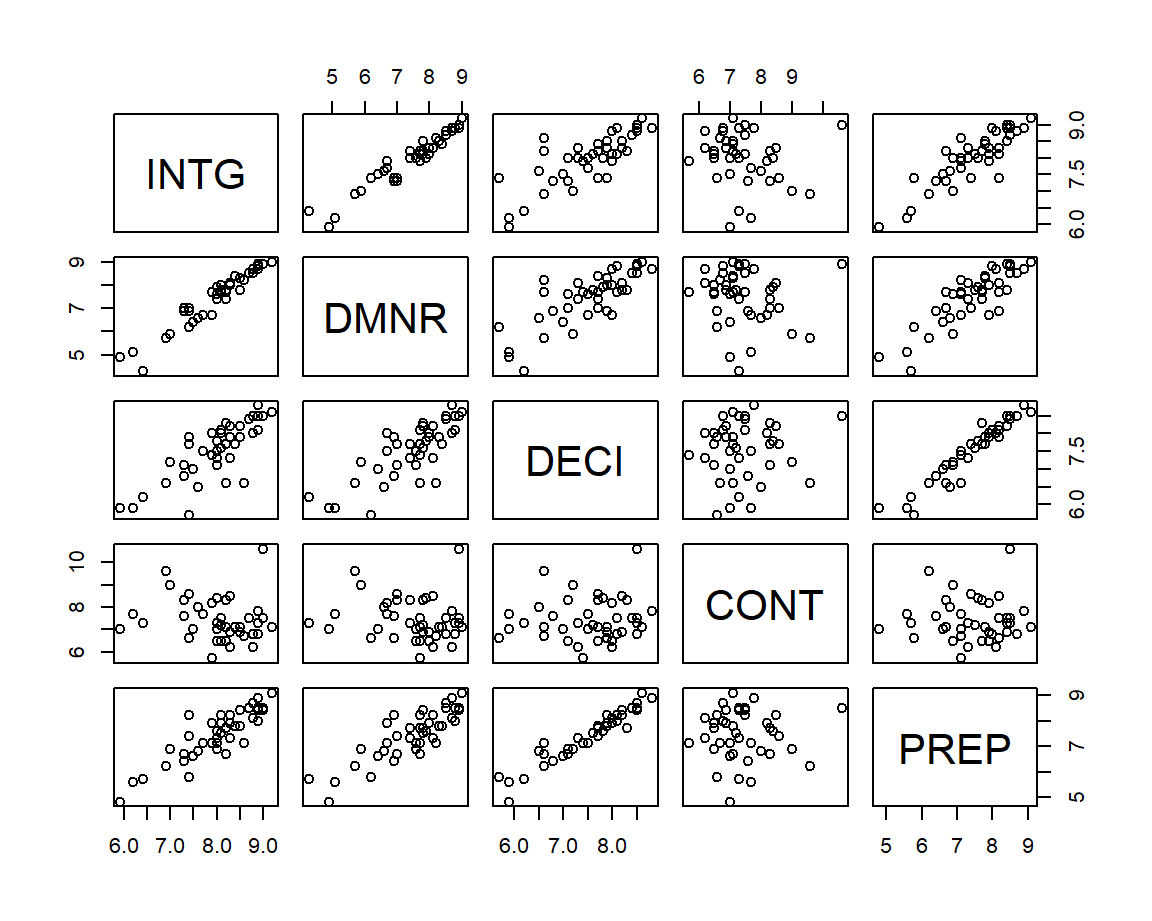
Figure 3.7: Ilustración de una matriz de dispersión.

La estructura de la función pairs con los argumentos más usuales se muestra a continuación:

pairs(x, labels, panel = points, ...,
      horInd = 1:nc, verInd = 1:nc,
      lower.panel = panel, upper.panel = panel,
      diag.panel = NULL, text.panel = textPanel,
      label.pos = 0.5 + has.diag/3, line.main = 3,
      cex.labels = NULL, font.labels = 1,
      row1attop = TRUE, gap = 1, log = "")

Los argumentos de la función pairs son:

• x: matriz o marco de datos con la información de las variables cuantitativas a incluir en la matriz de dispersión.
• labels: vector opcional con los nombres a colocar en la diagonal, por defecto se usan los nombres de columnas del objeto x.
• panel: función usual de la forma function(x,y,...) a ser usada para determinar el contenido de los páneles. Por defecto es points, indicando que se graficarán los puntos de los pares de variables. Es posible utilizar aquí otras funciones diseñadas por el usuario.
• ...: Indica que es posible agregar otros parámetros gráficos, tales como pch y col, con los cuales puede especificarse un vector de símbolos y colores a ser usados en los scatterplots.
• lower.panel, upper.panel: función usual de la forma function(x,y,...) para definir lo que se desea dibujar en los paneles abajo y arriba de la diagonal.
• diag.panel: función usual de la forma function(x,y,...) para definir lo que se desea dibujar en la diagonal.
• text.panel: Es opcional. Permite que una función: function(x, y, labels, cex, font, ...) sea aplicada a los paneles de la diagonal.
• label.pos: Para especificar la posición \(y\) de las etiquetas en el text panel.
• cex.labels, font.labels: Parámetros para la expansión de caracteres y fuentes a usar en las etiquetas de las variables.
• row1attop: Parámetro lógico con el cual se especifica si el gráfico para especificar si el diseño lucirá como una matriz con su primera fila en la parte superior o como un gráfico con fila uno en la base. Por defecto es lo primero.

Ejemplo

Dibujar una matriz de dispersión para las variables precio, área, número de alcobas y número de baños de la base de datos sobre apartamentos en Medellín.

A continuación se muestra el código usado para crear el gráfico solicitado. El objeto datos corresponde a la base de datos completa mientras que datos.num es el marco de datos sólo con las variables de interés precio, área, número de alcobas y número de baños.

url <- 'https://tinyurl.com/hwhb769'
datos <- read.table(file=url, header=T)
datos.num <- datos[, c('precio', 'mt2', 'alcobas', 'banos')]

pairs(datos.num)

Figure 3.8: Matriz de dispersión para las variables precio, área, número de alcobas y número de baños de la base de datos sobre apartamentos en Medellín.

En la Figura 3.8 se muestra la matriz de dispersión para las variables del marco de datos datos.num.

Ejemplo

Volver a construir la Figura 3.8 editando los nombres de las variables, usando cruces azules en lugar de puntos, en escala logaritmica, con marcas horizontales en el eje vertical y eliminando los diagramas de dispersión abajo de la diagonal.

Para obtener la nueva matriz de dispersión con los cambios solicitados se usa el siguiente código. En la Figura 3.9 se presenta la nueva matriz de dispersión.

pairs(datos.num, lower.panel=NULL, cex.labels=1.5, log='xy',
      main='Matriz de dispersión', las=1,
      labels=c('Precio', 'Área', 'Num alcobas', 'Num baños'),
      pch=3, cex=0.6, col='dodgerblue2')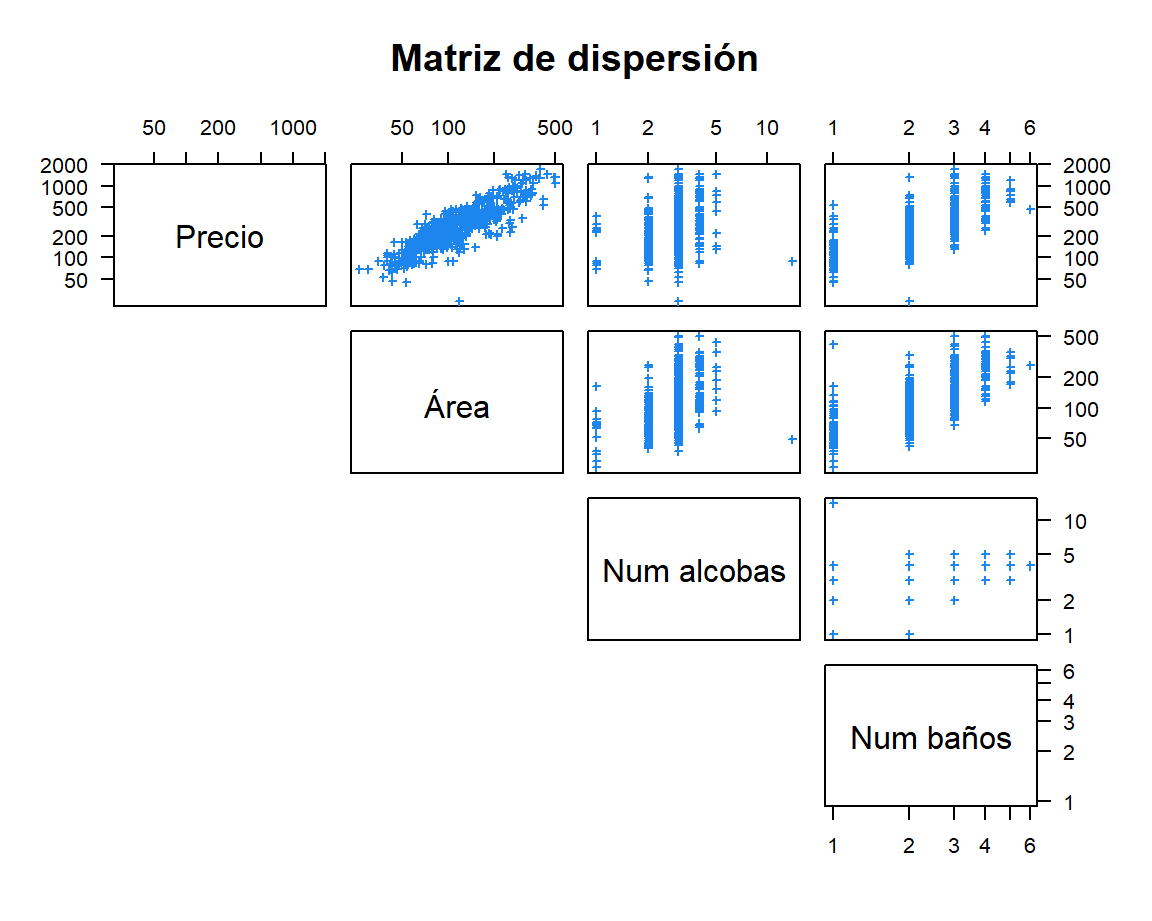

Figure 3.9: Matriz de dispersión modificando los parámetros adicionales de la función pairs.

Ejemplo

Construir una matriz de dispersión con las variables precio, área y avaluo para apartamentos que cumplan la condición \(100 m^2 < area < 130 m^2\). Adicionalmente, se deben diferenciar los apartamentos sin parqueadero con color rojo y los apartamentos con parqueadero con color verde.

Para crear una matriz de dispersión se puede tambien usar la base de datos original llamada datos que contiene todas las variables y usar una fórmula con la ayuda del operador ~ para indicar las variables de interés. La fórmula NO debe contener nada del lado izquierdo mientras que en el lado derecho se colocan todas las variables a considerar en la matriz de dispersión, por esta razón es que en el códido mostrado abajo se inicia con la instrucción ~ precio + mt2 + avaluo. Para incluir condiciones se usa el parámetro subset de la siguiente manera: subset=mt2 > 100 & mt2 < 130. A continuación el código completo para construir la matriz de dispersión solicitada.

col1 <- ifelse(datos$parqueadero == 'no', 'red', 'green3')
pairs(~ precio + mt2 + avaluo, data=datos,
      lower.panel=NULL, col=col1,
      subset=mt2 > 100 & mt2 < 130, pch=19, cex=0.8,
      main="Matriz de dispersión para aptos con 
      100 < área < 130 mt2")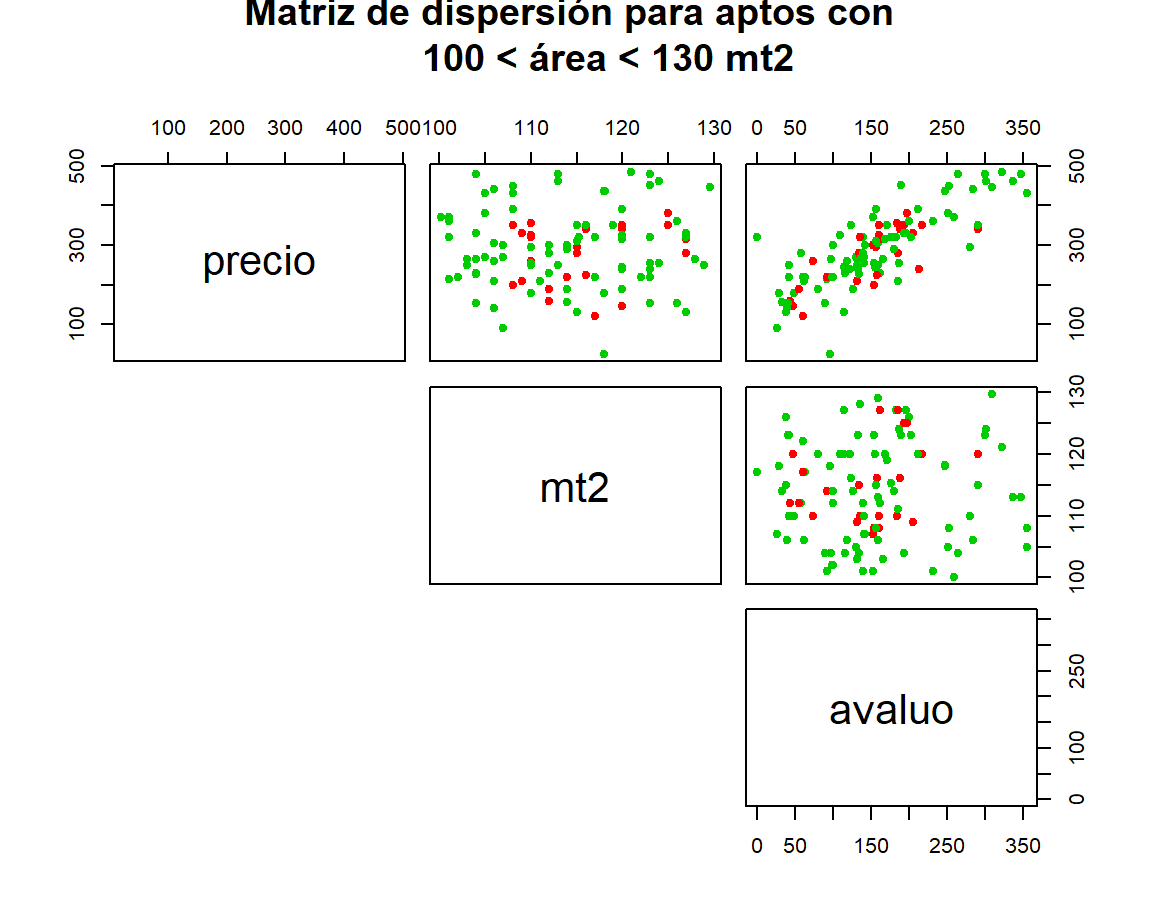

Figure 3.10: Matriz de dispersión con un subconjunto de los datos y con colores para identificar los puntos.

En la Figura 3.10 se presenta la matriz de dispersión solicitada, los puntos rojos representan los apartamento sin parqueadero mientras que los puntos verdes son los apartamento que si tienen parqueadero.

Ejemplo

¿Es posible agregar una leyenda a una matriz de dispersión?

Claro que es posible, se construye la matriz de dispersión y se deja en el lienzo del dibujo un espacio para colocar la leyenda. A continuación se muestra un ejemplo disponible en Stackoverflow. A continuación se muestra el código para el ejemplo y en la Figura 3.11 se presenta el resultado.

pairs(iris[1:4], main="Anderson's Iris Data -- 3 species",
      pch=21, bg=c("red", "green3", "blue")[iris$Species],
      oma=c(4, 4, 6, 12))
par(xpd=TRUE)
legend(0.85, 0.7, as.vector(unique(iris$Species)), bty='n',
       fill=c("red", "green3", "blue"))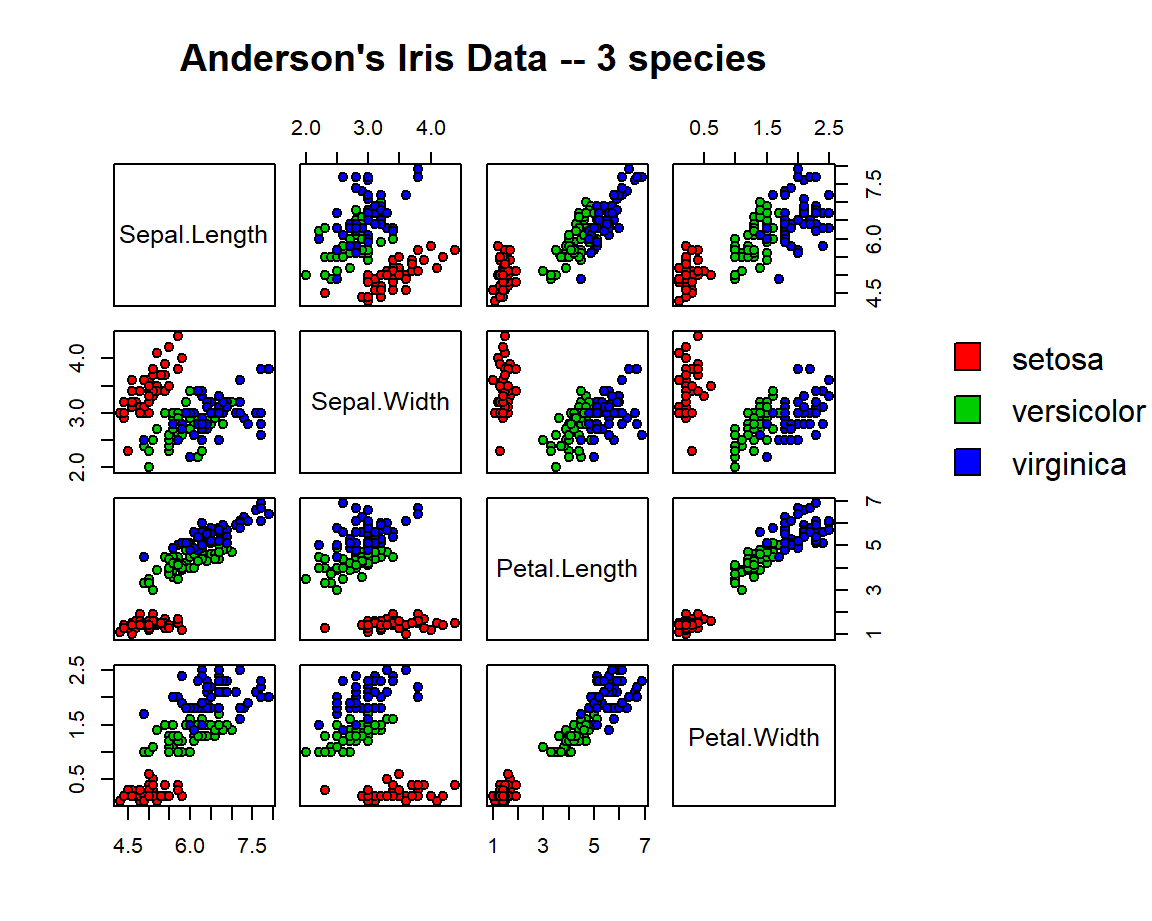

Figure 3.11: Matriz de dispersión con leyenda.

Ejemplo

¿Es posible modificar el contenido de los páneles de una matriz de dispersión?

Claro que es posible, para hacer esto se definen funciones que hagan lo que se desea ver tanto en la diagonal como arriba y abajo de la misma.

Como ejemplo vamos a construir una matriz de dispersión que cumpla:

• sobre la diagonal un diagrama de dispersión para las variables involucradas y la recta de regresión ajustada,
• en la diagonal un histograma para la variable,
• debajo de la diagonal el coeficiente de correlación entre las variables involucradas y usando un tamaño de fuente proporcional a la fuerza de correlación.

Para obtener esta matriz de dispersión especial se definen a continuación las funciones panel.reg, panel.hist y panel.cor, a continuación el código utilizado. Luego se usa la función pairs y se indica qué función debe actuar en cada uno de los parámetros upper.panel, diag.panel y lower.panel.

# Función para dibujar los puntos y agregar la recta de regresión
panel.reg <- function (x, y) 
{
  points(x, y, pch=20)
  abline(lm(y ~ x), lwd=2, col='dodgerblue2')
}

# Función para crear el histograma
panel.hist <- function(x, ...)
{
  usr <- par("usr"); on.exit(par(usr))
  par(usr = c(usr[1:2], 0, 1.5) )
  h <- hist(x, plot = FALSE)
  breaks <- h$breaks; nB <- length(breaks)
  y <- h$counts; y <- y/max(y)
  rect(breaks[-nB], 0, breaks[-1], y, col="dodgerblue2", ...)
}

# Función para obtener la correlación
panel.cor <- function(x, y, digits=2, prefix="", cex.cor)
{
  usr <- par("usr"); on.exit(par(usr))
  par(usr = c(0, 1, 0, 1))
  r <- abs(cor(x, y))
  txt <- format(c(r, 0.123456789), digits=digits)[1]
  txt <- paste(prefix, txt, sep="")
  if(missing(cex.cor)) cex <- 0.8/strwidth(txt)
  text(0.5, 0.5, txt, cex = cex * r)
}

pairs(datos.num,
      upper.panel = panel.reg,
      diag.panel = panel.hist,
      lower.panel = panel.cor)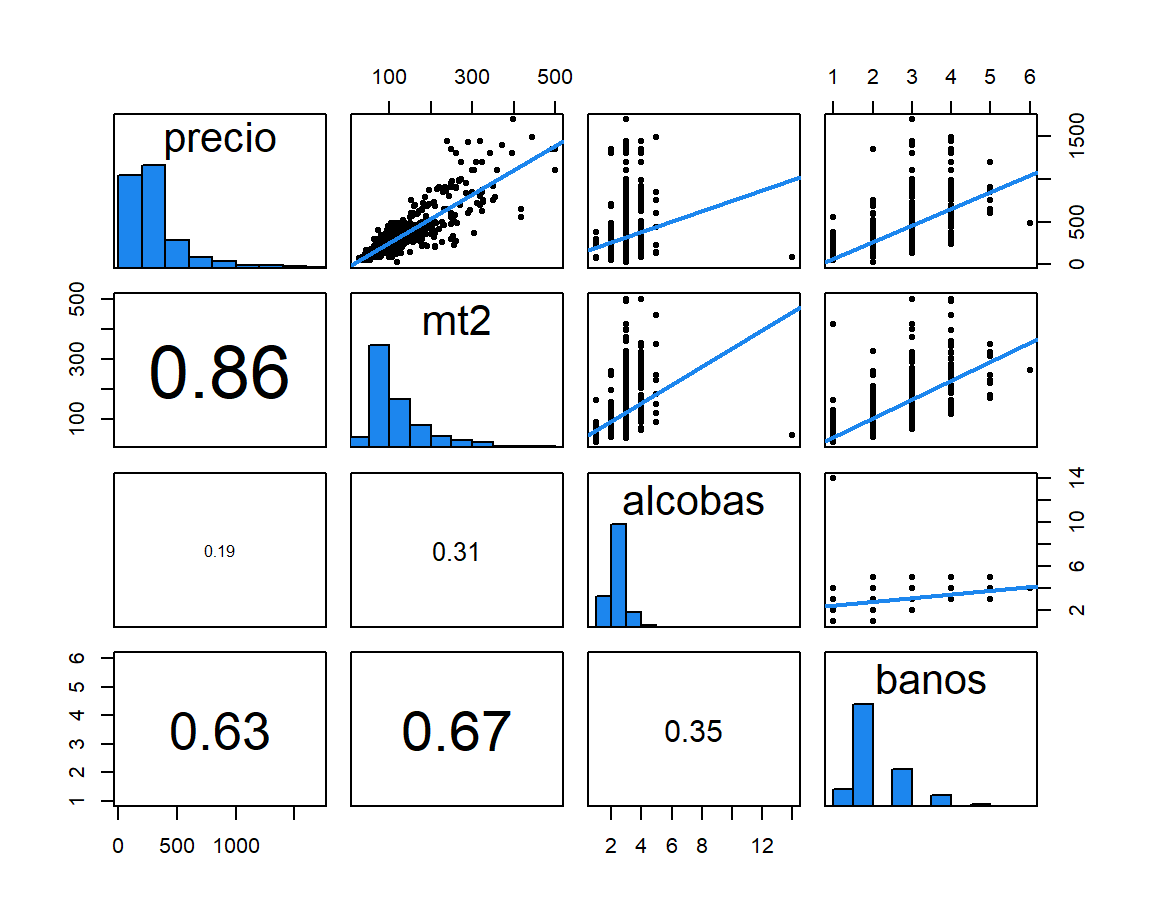

Figure 3.12: Matriz de dispersión con páneles modificados.

En la Figura 3.12 se presenta la matriz de dispersión con las modificaciones en cada uno de los páneles. Cualquier usuario puede modificar las funciones panel.reg, panel.hist y panel.cor para personalizar la apariencia de los contenidos.

La función panel.smooth está disponible en R para que el usuario pueda incluir arriba o abajo de la diagonal un diagrama de dispersión con una línea resultado de un ajuste suavizado. Abajo se muestra el código de cómo incluir la función panel.smooth y en la Figura 3.13 se muestra gráfico obtenido.

pairs(datos.num,
      upper.panel = panel.reg,
      diag.panel = panel.hist,
      lower.panel = panel.smooth)

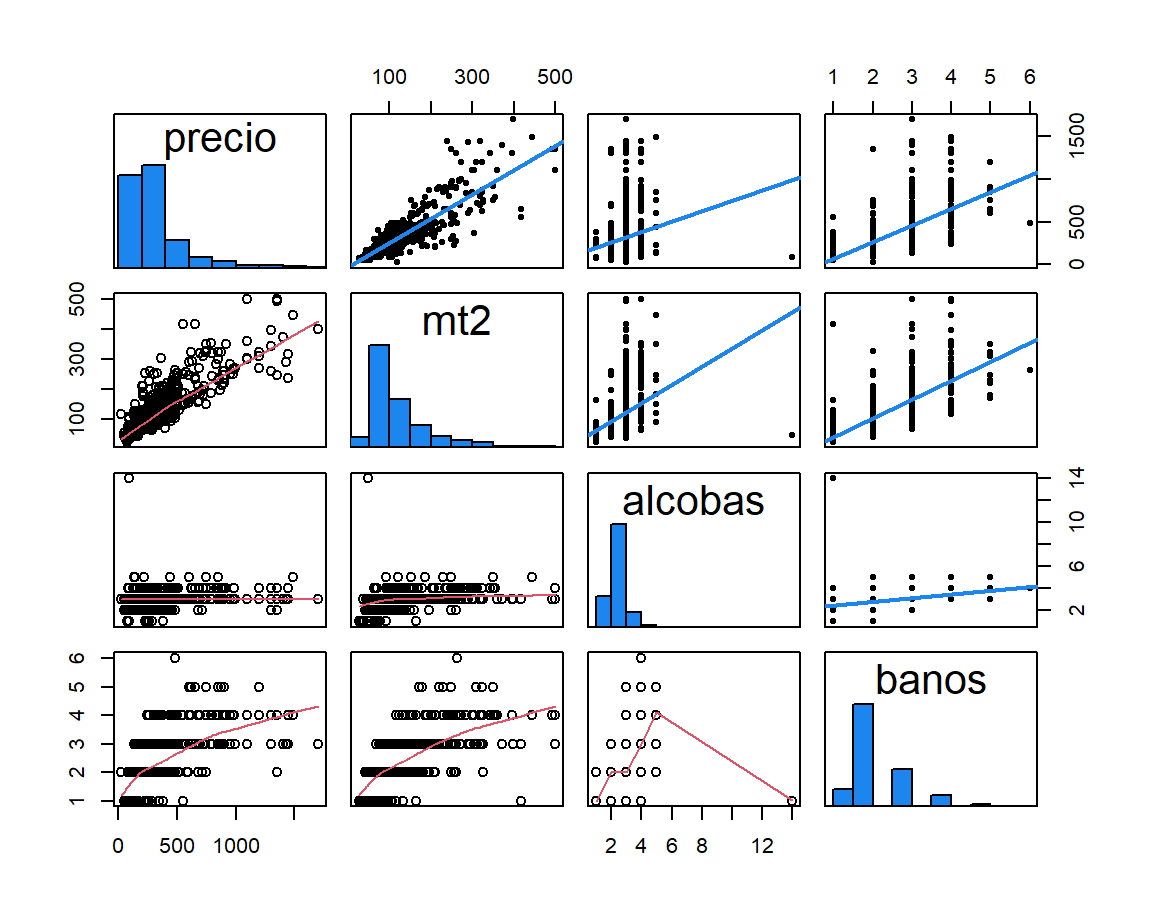
Figure 3.13: Matriz de dispersión usando la función panel.smooth.

Al construir un gráfico con pairs se recomienda no incluir demasiadas variables porque el gráfico se satura y no se pueden apreciar los patrones con facilidad. Se recomienda máximo 10 variables.

3.5 Función persp

La función persp dibuja superfices en tres dimensiones y es posible rotar la superficie para obtener una perpectiva apropiada. La estructura de la función persp con los argumentos más usuales se muestra a continuación:

persp(x, y, z, main, sub, theta, phi, r, col,
      border, box, axes, nticks)

Los argumentos de la función plot son:

• x: vector numérico con los valores de \(x\) donde fue evaluada la función o superficie.
• y: vector numérico con los valores de \(y\) donde fue evaluada la función o superficie.
• z: matriz que contiene las alturas \(z\) de la supercifie para cada combinación de \(x\) e \(y\).
• main: vector numérico con las coordenadas del eje vertical.
• sub: vector numérico con las coordenadas del eje vertical.
• theta, phi: ángulo para la visión de la superficie, theta para la dirección azimutal y phi para latitud. Ver Figura 3.14 para una ilustración de los ángulos.
• r: distancia entre el centro de la caja de dibujo al punto de vista.
• col: color de la superficie.
• border: color para el borde de la superficie.
• box: valor lógico para indicar si se quiere dibujar la caja que contiene la superficie, por defecto es TRUE.
• axes: valor lógico para indicar si se desean marcas en los ejes y nombres de los ejes, por defecto es TRUE. Si box='FALSE' no aparecen marcas ni nombres de los ejes.
• expand: factor de expansión aplicado a los valores en el eje z.
• ticktype: tipo de marcas a colocar en los ejes, simple no dibuja nada y detailed coloca números a los ejes.
• nticks: número aproximado de marcas en los ejes.

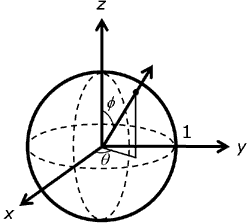
Figure 3.14: Ilustración de los ángulos theta y phi para la función persp. Figura tomada de https://i-msdn.sec.s-msft.com/dynimg/IC412528.png

Ejemplo

Dibujar la superficie asociada a la función \(f(x, y)=sen(x^2+y^2)\) para \(-2 \leq x \leq2\) y \(-2 \leq y \leq2\). Usar 4 combinaciones de los parámetros theta y phi para obtener un buen punto de vista de la superficie.

Lo primero que se debe hacer es crear la función \(f(x, y)\) la cual se va a llamar fun. Luego se definen los vectores x e y tomando por ejemplo 25 puntos equiespaciados en el intervalo \([-2, 2]\). Luego se usa la función outer para crear la rejilla o matriz que contiene los valores de \(f(x, y)\) para cada combinación de x e y, los resultados se almacenan en el objeto z. Por último se dibujan 4 perspectivas de la función variando los parámetros theta y phi de la función persp. A continuación el código utilizado.

fun <- function(x, y)   sin(x^2 + y^2)
x <- seq(from=-2, to=2, length.out=25)
y <- seq(from=-2, to=2, length.out=25)
z <- outer(x, y, fun)

par(mfrow=c(2, 2), mar=c(1, 1, 2, 1))
persp(x, y, z, zlim=c(-1, 1.5), theta=0, phi=0, col='aquamarine',
      main='(A) theta=0, phi=0')
persp(x, y, z, zlim=c(-1, 1.5), theta=15, phi=15, col='lightpink',
      main='(B) theta=15, phi=15')
persp(x, y, z, zlim=c(-1, 1.5), theta=45, phi=30, col='yellow1',
      main='(c) theta=45, phi=30')
persp(x, y, z, zlim=c(-1, 1.5), theta=60, phi=50, col='lightblue',
      main='(D) theta=60, phi=50')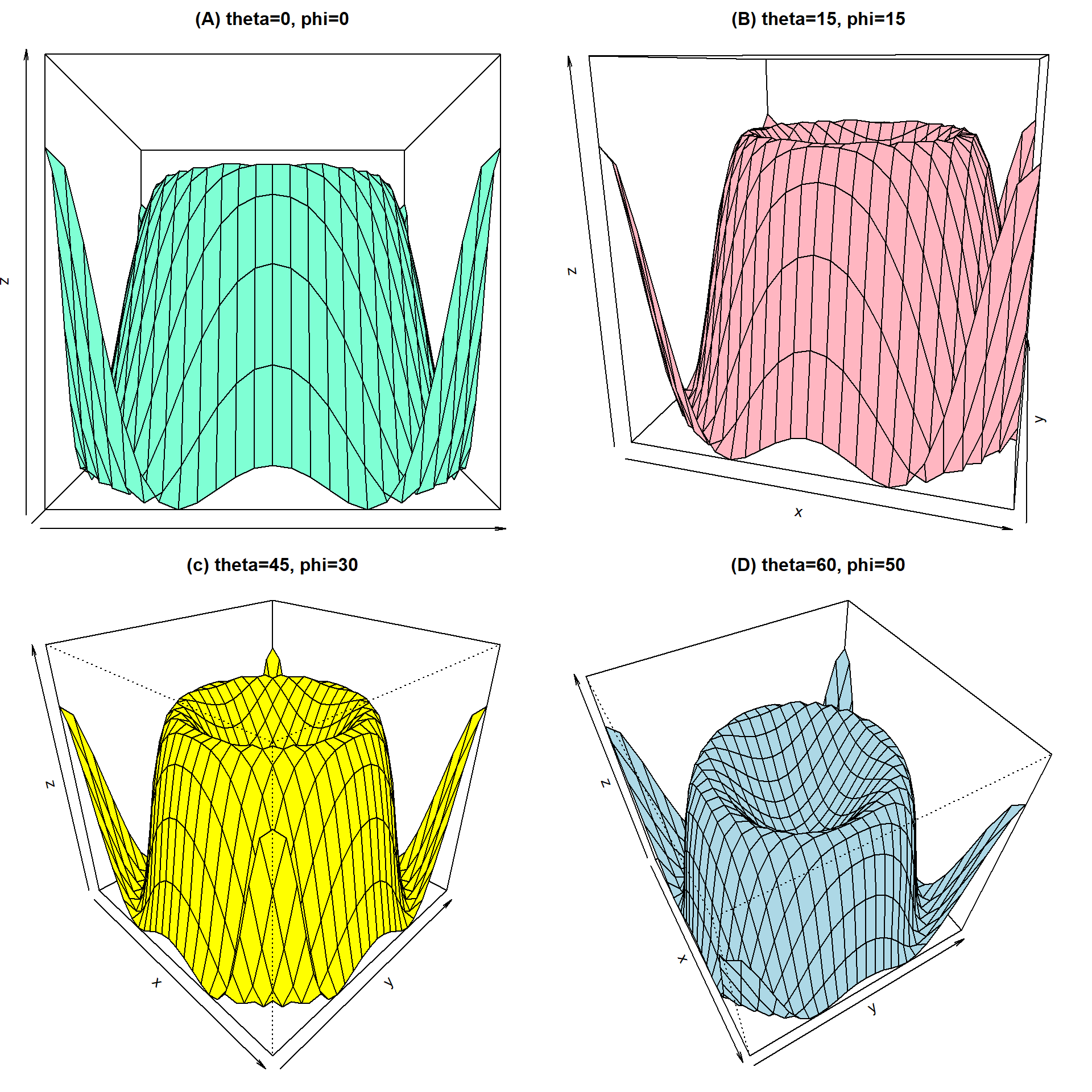

Figure 3.15: Superficie generada con persp y diferentes valores de theta y phi.

En la Figura 3.15 se presentan las 4 perspectivas de la función \(f(x, y)=sen(x^2+y^2)\). De los 4 páneles se nota que (C) y (D) muestran mejor la superficie de interés.

Al aumentar el valor del parámetro length.out en la creación de los vectores x e y se obtendrá una rejilla más tupida, se recomienda modificar este valor para obtener una superficie apropiada.

Ejemplo

Dibujar la superficie de una distribución normal bivariada con vector de medias \(\boldsymbol{\mu}=(5, 12)^\top\), varianzas unitarias y covarianza con valor de -0.8. Explorar el efecto de los parámetros ticktype, nticks, expand, axes y box.

Primero se define el vector de medias y la matriz de varianzas y covarianzas, luego se carga el paquete mvtnorm que contiene la función dmvnorm que calcula la densidad dado el vector de medias y la matriz de varianzas y covarianzas. Se construye la función fun y se vectoriza para luego obtener las alturas de la superficie con la ayuda de outer. Por último se dibujan tres perspectivas diferentes para la densidad modificando los parámetros ticktype, nticks, expand, axes y box, a continuación el código usado.

media <- c(5, 12)
varianza <- matrix(c(1, -0.8, -0.8, 1), ncol=2)

require(mvtnorm)
fun <- function(x, y) dmvnorm(c(x, y), mean=media, sigma=varianza)
fun <- Vectorize(fun)

x <- seq(from=2, to=8, length.out=30)
y <- seq(from=9, to=15, length.out=30)
z <- outer(x, y, fun)

par(mfrow=c(1, 3), mar=c(1, 1, 2, 1))
persp(x, y, z, theta=30, phi=30, ticktype = "detailed", nticks=4)
persp(x, y, z, theta=30, phi=30, col='salmon1', expand=0.5, axes=FALSE)
persp(x, y, z, theta=30, phi=30, col='springgreen1', expand=0.2, box=FALSE)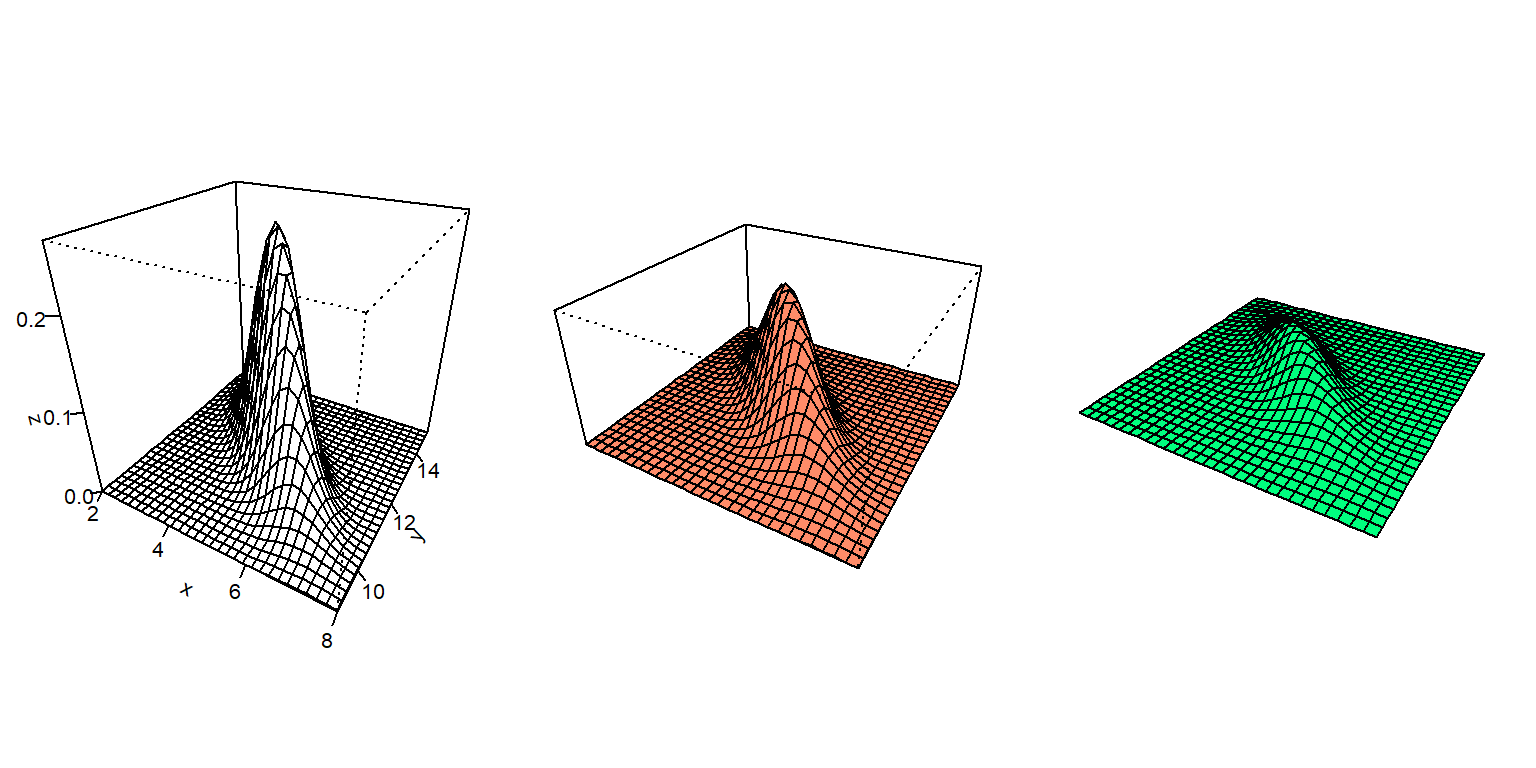

Figure 3.16: Distribución normal bivariada.

En la Figura 3.16 se presentan las 3 perspectivas para la densidad. Note los efectos que ticktype, nticks, expand, axes y box tienen sobre los dibujos de las perspectivas.

3.6 Función contour

La función contour dibuja gráficos contornos. La estructura de la función contour con los argumentos más usuales se muestra a continuación:

contour(x, y, z,
        xlim, ylim, zlim,
        levels, nlevels=20, col)

Los argumentos de la función son:

• x, y: vectores numéricos en los cuales se evaluó la función de interés para construir el objeto z. Ambos vectores deben estar ordenados.
• z: matriz con las alturas de la función de interés, por lo general creada con la función outer.
• xlim, ylim, zlim: límites de los ejes x, y e z respectivamente.
• nlevels: número aproximado de niveles o cortes en la superficie a representar.
• col: color a usar en las líneas de contornos.

La función contour tiene otros parámetros adicionales que el lector puede consultar en la ayuda usando help(contour).

Ejemplo

Generar una muestra aleatoria de 50 observaciones de una distribución normal con parámetros \(\mu=170\) y \(\sigma^2=25\). Dibujar un gráfico de contornos para la superficie de log-verosimilitud.

La muestra aleatoria se genera con el siguiente código.

y <- rnorm(n=50, mean=170, sd=5)  # sd es desviación

Para dibujar los contornos solicitados se debe primero construir la función de log-verosimilitud llamada ll. A continuación el código para crear ll, mayores detalles de cómo construir funciones de log-verosimilitud se pueden consultar en Hernández and Usuga (2018).

ll <- function(a, b) sum(dnorm(x=y, mean=a, sd=b, log=TRUE))
ll <- Vectorize(ll)  # Para vectorizar la función

Una vez construída la función ll se deben construir los vectores con las coordenadas horizontal y vertical donde se evalua la función ll. En el código mostrado abajo se tienen dos vectores xx e yy obtenidos como secuencias desde el menor valor hasta el mayor valor para cada uno de los parámetros \(\mu\) y \(\sigma\) de la distribución normal, el valor by=0.5 indica el tamaño de paso de la secuencia. Luego se construye la matriz zz usando la función outer evaluando ll en xx e yy. Por último la función contour se aplica sobre los elementos xx, yy e zz. En la Figura 3.17 se muestra el gráfico de contornos con aproximadamente 50 niveles.

xx <- seq(from=160, to=180, by=0.5)
yy <- seq(from=3, to=7, by=0.5)
zz <- outer(X=xx, Y=yy, ll)
contour(x=xx, y=yy, z=zz, nlevels=50,
        col=gray(0.3), lwd=2, lty='solid',
        xlab=expression(mu), ylab=expression(sigma))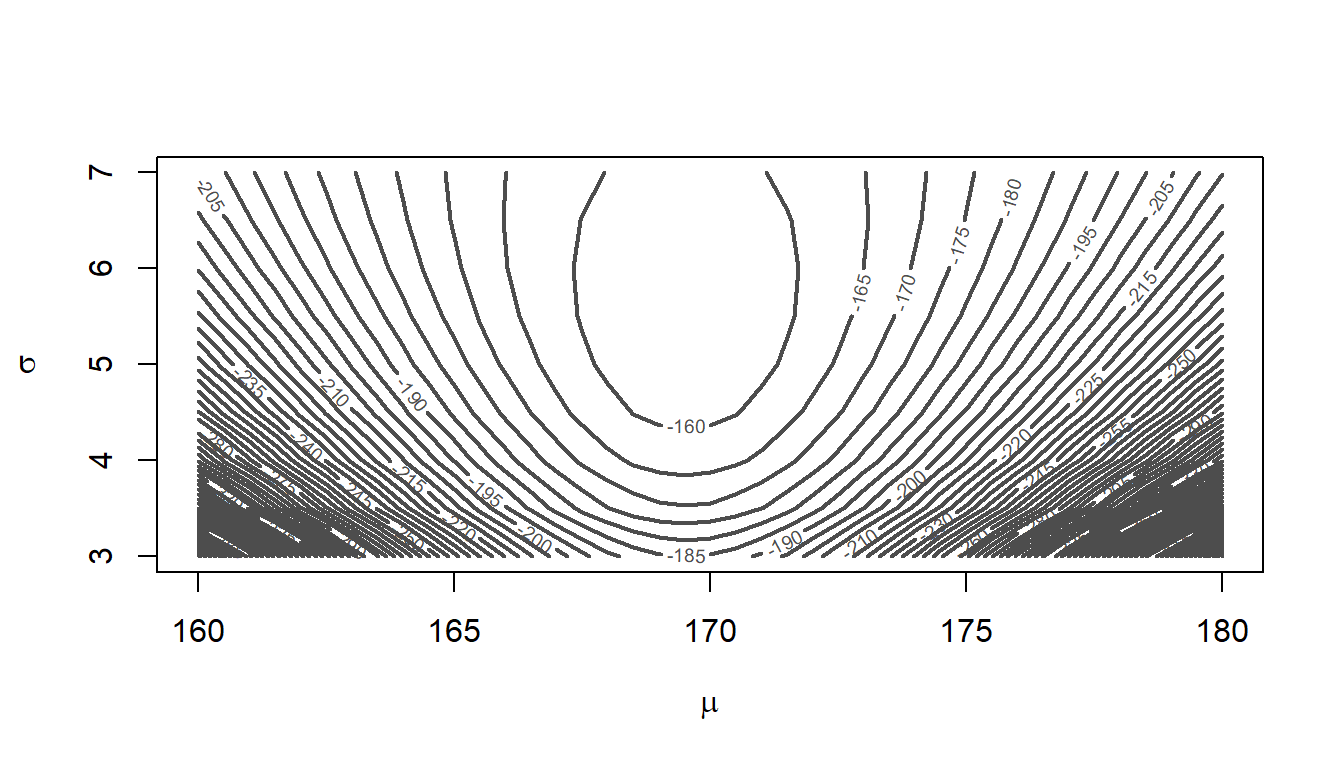

Figure 3.17: Gráfico de contornos para la función de log-verosimilitud para el ejemplo sobre normal.

3.7 Función filled.contour

La función filled.contour dibuja gráficos contornos pero usando una paleta de colores, este tipo de representación se denomina gráfico de nivel. La estructura de la función filled.contour con los argumentos más usuales se muestra a continuación:

filled.contour(x, y, z,
               xlim, ylim, zlim,
               levels, nlevels=20,
               color.palette=cm.colors, col)

Los argumentos de la función son:

• x, y: vectores numéricos en los cuales se evaluó la función de interés para construir el objeto z. Ambos vectores deben estar ordenados.
• z: matriz con las alturas de la función de interés, por lo general creada con la función outer.
• xlim, ylim, zlim: límites de los ejes x, y e z respectivamente.
• nlevels: número aproximado de niveles o cortes en la superficie a representar.
• color.palette: paleta de colores a usar. Por defecto es cm.colors pero el usuario puede elegir entre heat.colors, terrain.colors o topo.colors.

La función filled.contour tiene otros parámetros adicionales que el lector puede consultar en la ayuda usando help(filled.contour).

Ejemplo

Abajo se muestra el código para crear un gráfico de nivel usando los datos del ejemplo anterior. Observe que las figuras 3.17 y 3.18 son bastante similares.

filled.contour(x=xx, y=yy, z=zz, nlevels=20,
               xlab=expression(mu), ylab=expression(sigma),
               color = topo.colors)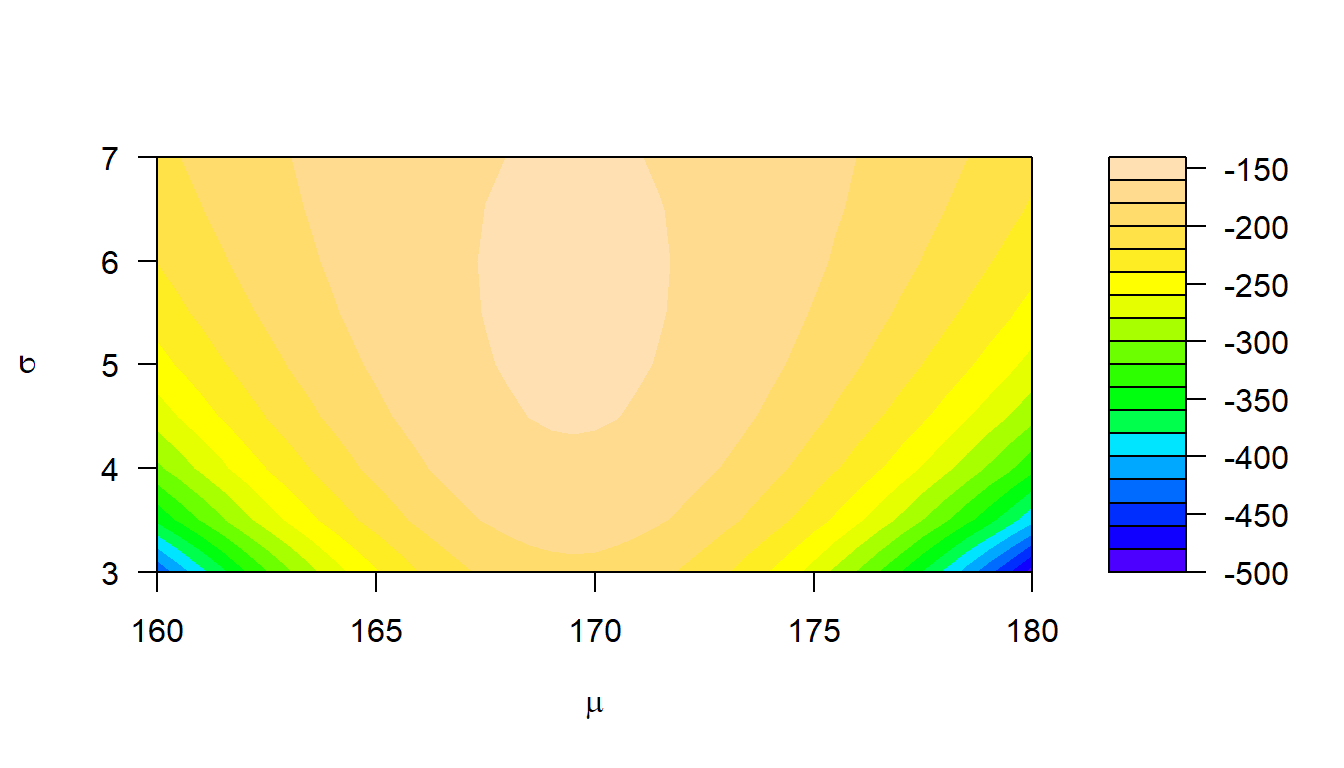

Figure 3.18: Gráfico de nivel para la función de log-verosimilitud para el ejemplo sobre normal.

Ejemplo

¿Es posible crear un gráfico de contornos y de niveles en la misma figura?

Claro que si, abajo se muestra el código para crear primero el gráfico de niveles (en colores) y luego superponer el gráficos de contornos (las lineas). En la Figura 3.19 se muestra el gráfico resultante.

filled.contour(x=xx, y=yy, z=zz,  nlevels=20,
               color.palette = topo.colors, 
               plot.axes=contour(xx, yy, zz, nlevels=20, add=TRUE))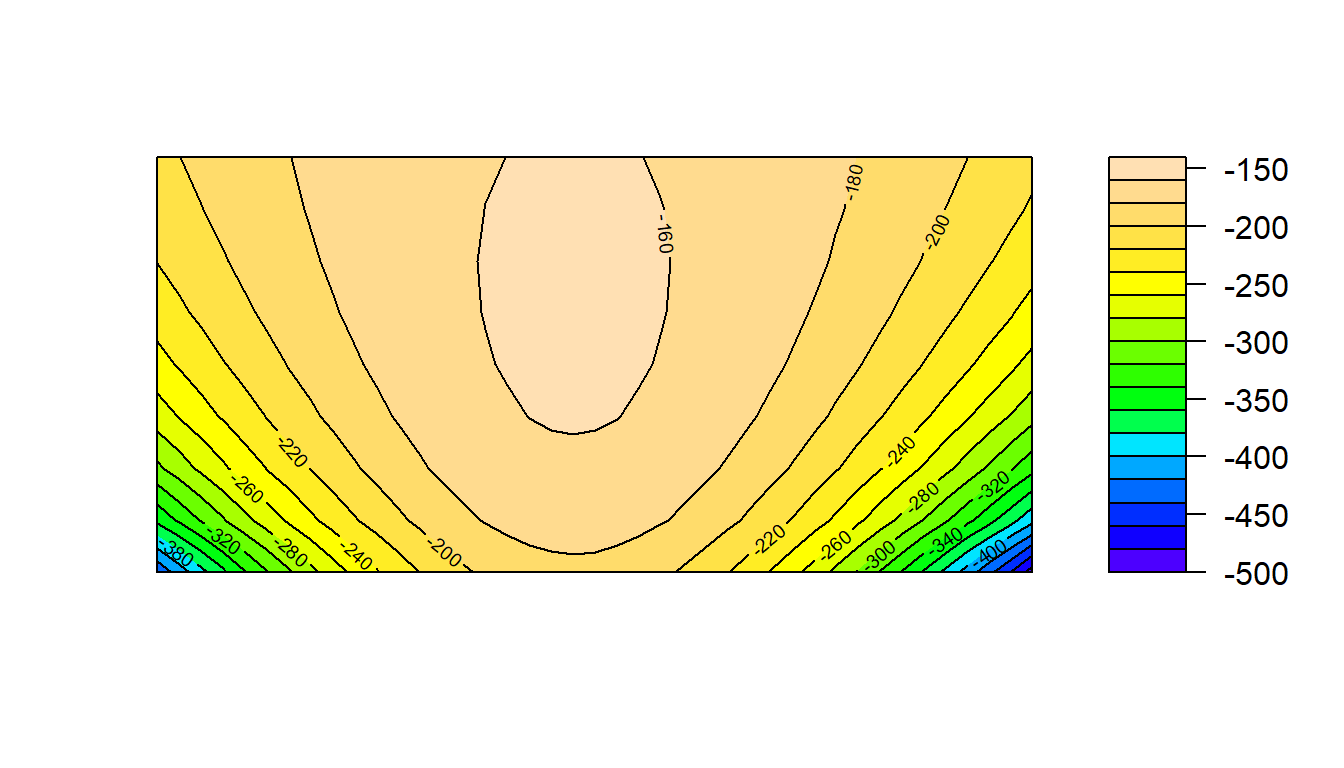

Figure 3.19: Gráfico de nivel y contornos para la función de log-verosimilitud para el ejemplo sobre normal.

3.8 Función image

La función image dibuja un gráfico de calor similar al obtenido con la función filled.contour. La estructura de la función image con los argumentos más usuales se muestra a continuación:

image(x, y, z)

Los argumentos de la función son:

• x, y: vectores numéricos en los cuales se evaluó la función de interés para construir el objeto z. Ambos vectores deben estar ordenados.
• z: matriz con las alturas de la función de interés, por lo general creada con la función outer.

Ejemplo

Para la muestra aleatoria obtenida en el ejemplo anterior, dibujar un gráfico con image para la superficie de log-verosimilitud.

Usando los objetos xx, yy e zz creados en el ejemplo anterior se puede construir el gráfico solicitado, a continuación el código utilizado. En la Figura 3.20 se muestra el gráfico.

image(x=xx, y=yy, z=zz,
      xlab=expression(mu), ylab=expression(sigma))

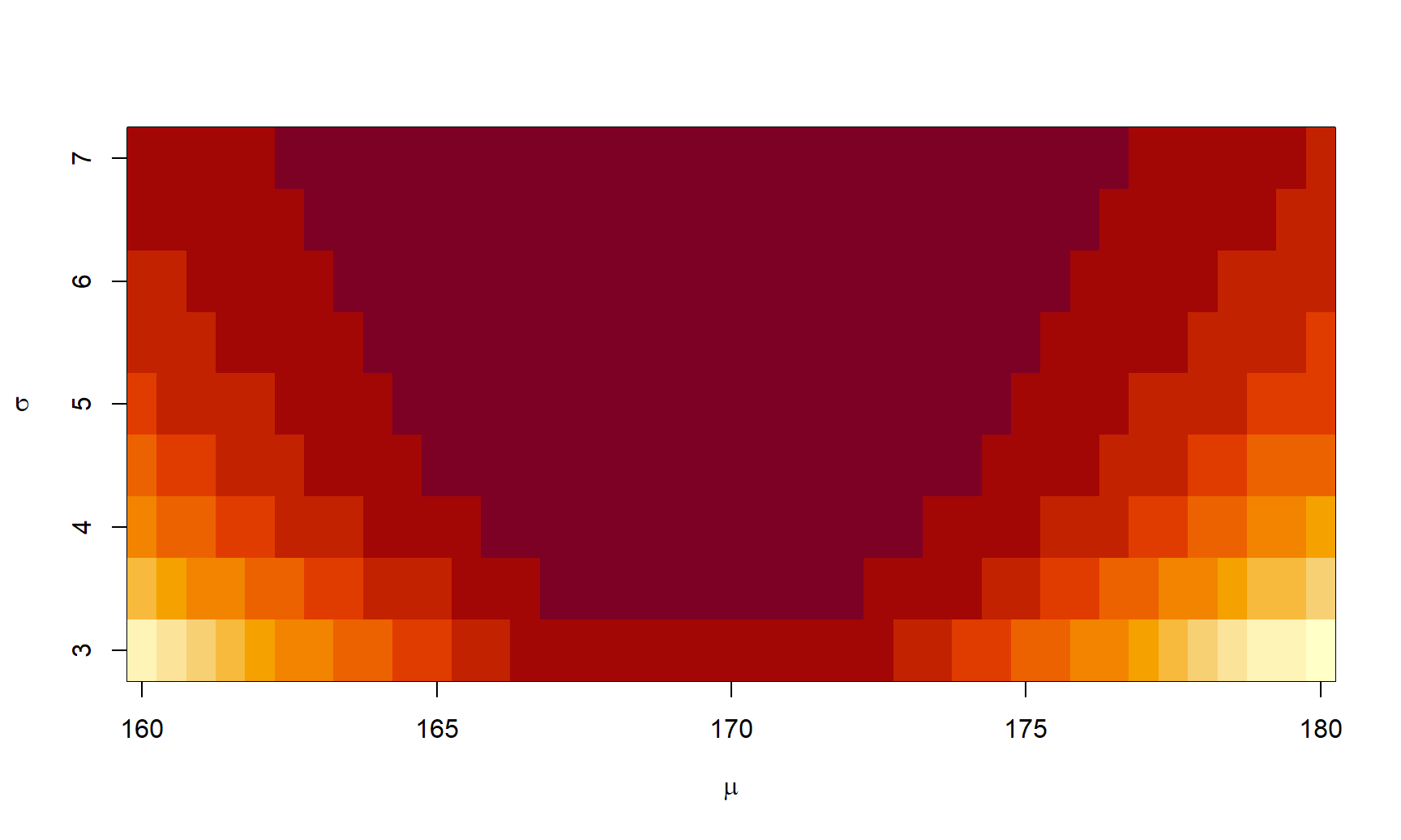
Figure 3.20: Gráfico para la función de log-verosimilitud para el ejemplo sobre normal.

3.9 Función kde2d

La función kde2d pertenece al paquete MASS y es utilizada para crear densidades para dos variables cuantitativas. La estructura de la función kde2d con los argumentos más usuales se muestra a continuación:

kde2d(x, y, h, n = 25, lims = c(range(x), range(y)))

Los argumentos de la función son:

• x: vector con la variable para el eje X.
• y: vector con la variable para el eje Y..
• h: vector con los anchos de banda en las direcciones X e Y.
• n: número de puntos para construir la rejilla.
• lims: límites del rectángulo de datos a considerar, debe ser un vector de la forma c(xl, xu, yl, yu). Este parámetro por defecto es c(range(x), range(y)).

Ejemplo

La base de datos medidas del cuerpo cuenta con 6 variables registradas a un grupo de 36 estudiantes de la universidad, dos de esas variables son la altura y el peso corporal. Se desea construir un gráfico de densidad bivariada para altura y peso.

El código mostrado a continuación hace la lectura de la base de datos y luego se construyen dos densidades, la primera con n=5 y la segunda con n=50, esto para ver el efecto del parámetro n.

url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)

require(MASS)  # Se debe cargar este paquete
f1 <- kde2d(x=datos$peso, y=datos$altura, n=5)
f2 <- kde2d(x=datos$peso, y=datos$altura, n=50)

En el código mostrado a continuación se dibujan las dos densidades usando un gráfico de calor usando la función image.

par(mfrow=c(1, 2))
image(f1, xlab='Peso', ylab='Estatura', main='n=5')
image(f2, xlab='Peso', ylab='Estatura', main='n=50')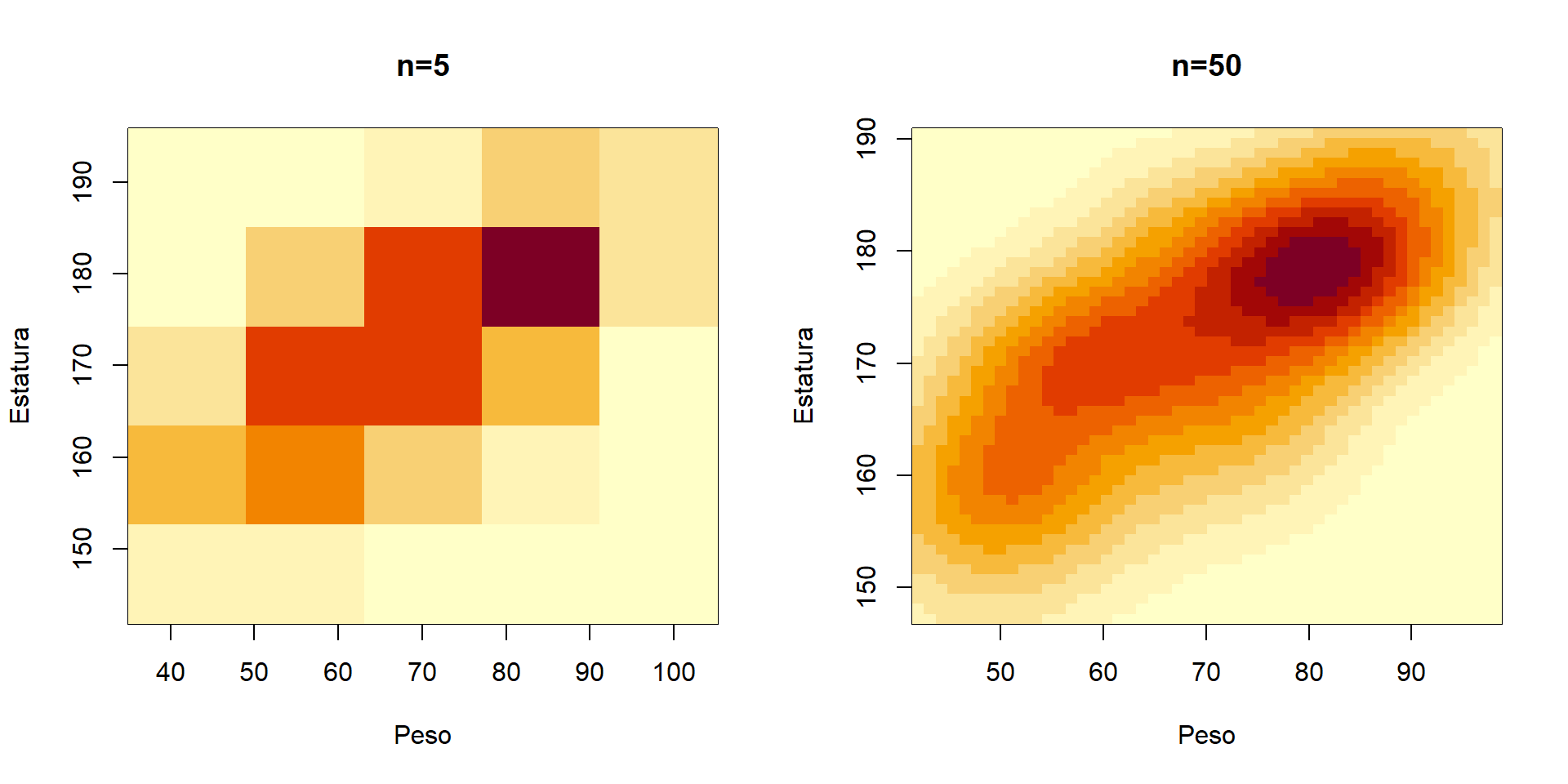

Figure 3.21: Gráfico de densidad bivariada para el peso corporal y la estatura de un grupo de estudiantes. A la izquierda la densidad con n=5 y a la derecha con n=50.

3.10 Función interaction.plot

La función interaction.plot dibuja gráficos de interacción. La estructura de la función interaction.plot con los argumentos más usuales se muestra a continuación:

interaction.plot(response, x.factor, trace.factor, fun,
                 legend, trace.label)

Los argumentos de la función son:

• response: vector numérico con la variable respuesta.
• x.factor: factor 1 a ubicar en el eje horizontal.
• trace.factor: factor 2 para diferenciar las líneas.
• fun: función a aplicar para a response para cada combinación de x.factor y trace.factor.
• legend: valor lógico para incluir o no leyenda.
• trace.label: nombre a colocar en la leyenda.

La función interaction.plot tiene otros parámetros adicionales que el lector puede consultar en la ayuda usando help(interaction.plot).

Ejemplo

Se realizó un experimento para determinar cómo influye el material de la batería y la temperatura del medio ambiente sobre la duración en horas de la batería. Se desea construir un gráfico de interacción entre Temperatura y Material para ver el efecto sobre la duración promedio de las baterías. Los datos y el código para generar el gráfico solicitado se muestran a continuación.

horas <- c(130, 155, 74, 180, 150, 188, 159, 126, 138, 110, 168, 
           160, 34, 40, 80, 75, 136, 122, 106, 115, 174, 120, 150, 
           139, 20, 70, 82, 58, 25, 70, 58, 45, 96, 104, 82, 60)

temperatura <- rep(c(15, 70, 125), each=12)
material    <- rep(1:3, each=4, times=3)

interaction.plot(x.factor=temperatura, trace.factor=material,
                 response=horas, trace.label='Material',
                 xlab='Temperatura',
                 ylab='Duración promedio (horas)',
                 col=c('dodgerblue3', 'chartreuse4', 'salmon3'),
                 fun=mean, lwd=2, las=1, fixed=T)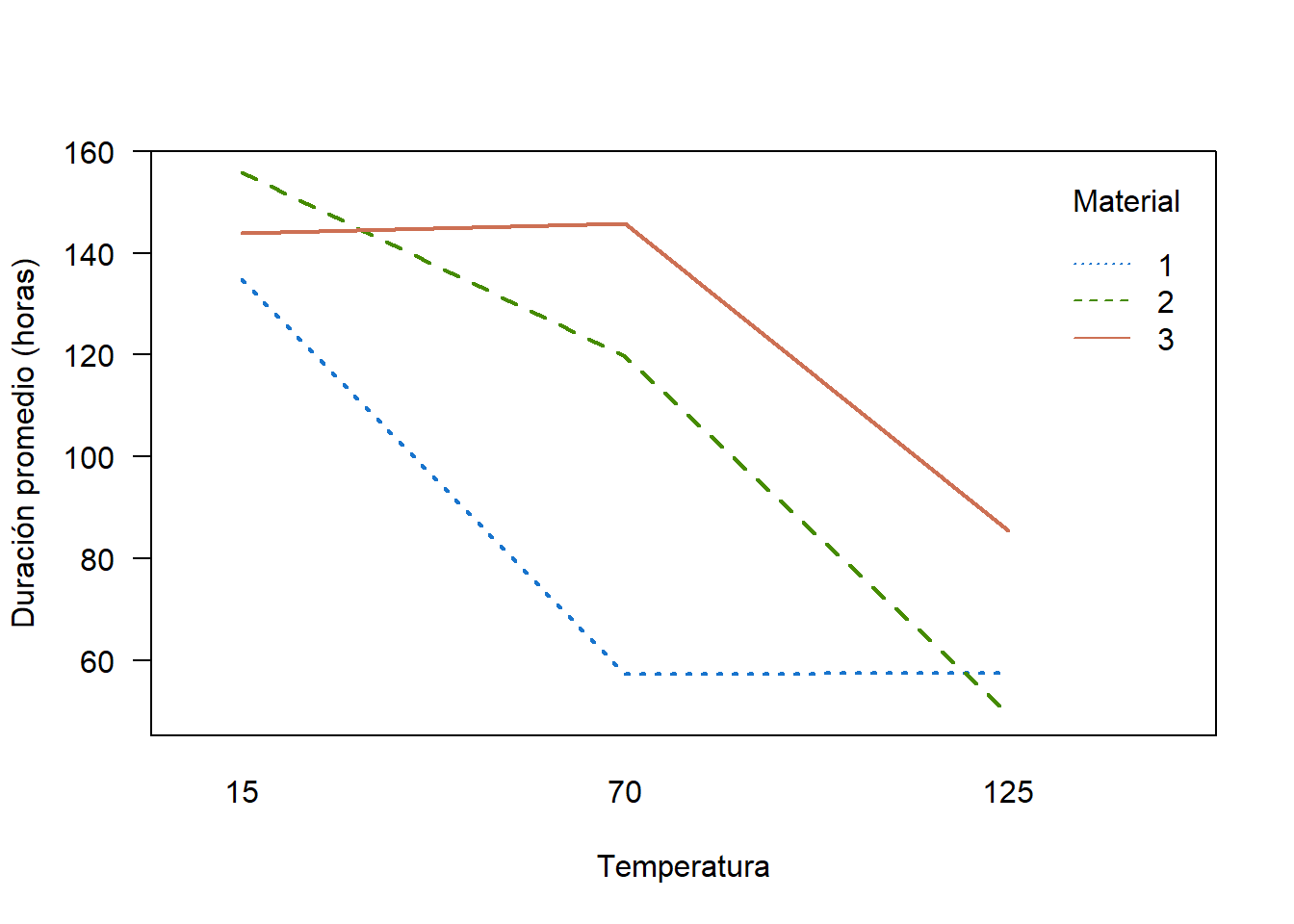

Figure 3.22: Gráfico de interacción entre Temperatura y Material sobre la duración promedio de las baterías.

3.11 Gráfico de espagueti

Los gráficos de espagueti son usados para representar la evolución de una variable medida para un grupo de sujetos en diferentes momentos del tiempo. La función interaction.plot se puede usar para obtener este tipo de gráficos, a continuación un ejemplo.

Ejemplo

El ejemplo aquí presentado fue tomado de este enlace. El objetivo es crear un gráfico de espagueti para mostrar la evolución de la variable tolerancia a través del tiempo para cada uno de los 16 individuos estudiados. El código para descargar la base de datos y construir el gráfico se muestran a continuación.

dt <- read.table("https://stats.idre.ucla.edu/stat/r/faq/tolpp.csv",
                 sep=",", header=T)

require(gplots)           # Paquete especial para crear una paleta
palette(rich.colors(16))  # de 16 colores diferentes y suaves

interaction.plot(response=dt$tolerance,
                 x.factor=dt$time, col=1:16, lwd=2,
                 trace.factor=dt$id, las=1, lty=1, 
                 xlab="Tiempo", ylab="Tolerancia", legend=F)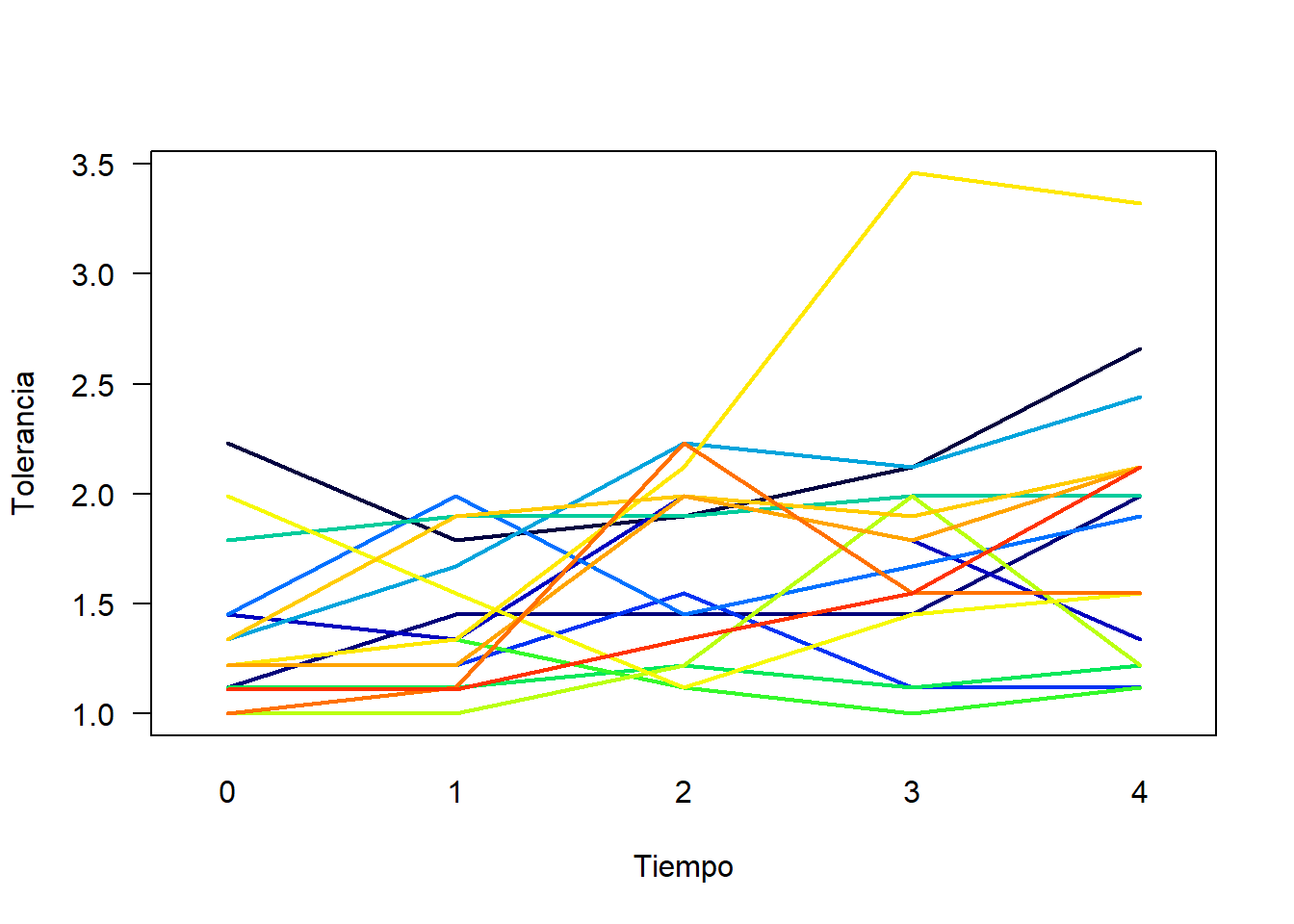

Figure 3.23: Gráfico de espagueti para ver la evolución de la variable tolerancia.

References

Hernández, F., and O. Usuga. 2018. Manual de R. Medellín, Colombia. https://fhernanb.github.io/Manual-de-R/.