6 Funciones auxiliares
En este capítulo se presentan funciones auxiliares que son útiles para complementar los gráficos generados en R.
6.1 Función segments
Esta función es muy útil para digujar segmentos. La estructura de la función se muestra a continuación.
Los argumentos de la función son:
xo, yo: coordenadas del punto de inicio del segmento.x1, y1: coordenadas del punto de fin del segmento....: otros parámetros gráficos.
A continuación de muestra el código para dibujar con segmentos la sigla de la Universidad Nacional de Colombia (UN), en la Figura 6.1 se puede ver el resultado.
plot(c(-11, 3), c(-10, 10), type="n", xlab="", ylab="")
grid()
segments(-9, 9, -9, -9, lwd=4, col=3)
segments(-9, -9, -5, -9, lwd=4, col=3)
segments(-5, -9, -5, 9, lwd=4, col=3)
segments(-4, -9, -4, 9, lwd=4)
segments(-4, 9, 0, -9, lwd=4)
segments(0, -9, 0, 9, lwd=4)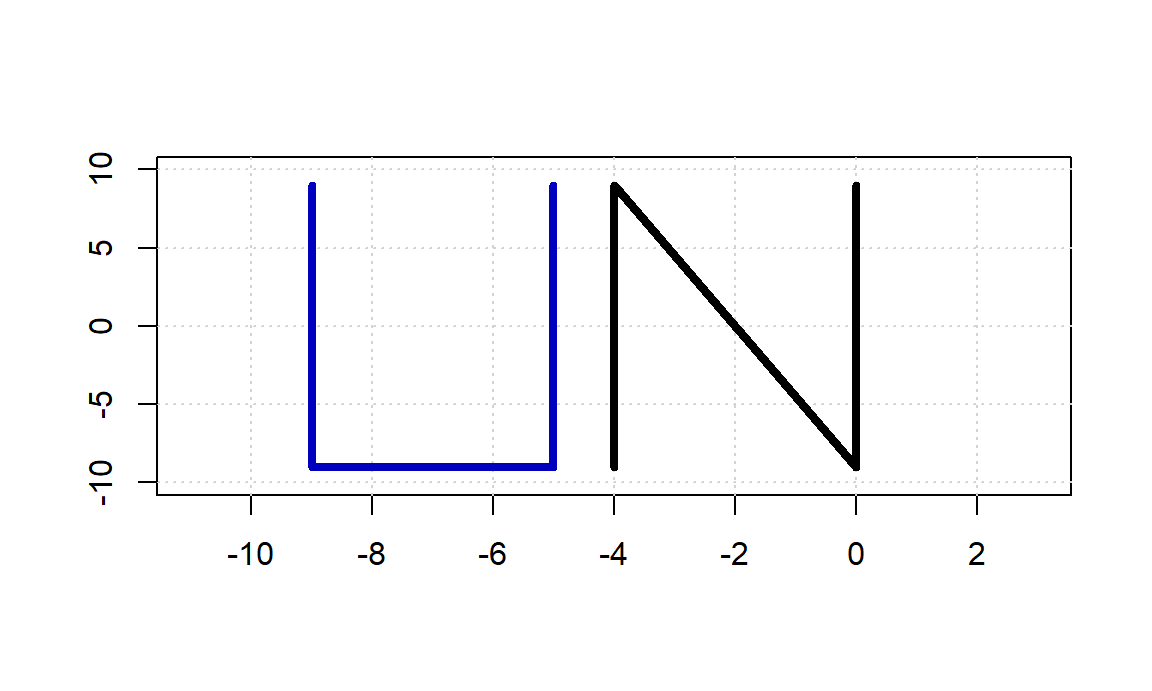
Figure 6.1: Ejemplos de segmentos.
6.2 Función rect
Esta función es muy útil para digujar rectángulos. La estructura de la función se muestra a continuación.
Los argumentos de la función son:
xleft: vector o escalar con la posición de x a izquierda.ybottom: vector o escalar con la posición de y abajo.xright: vector o escalar con la posición de x a derecha.ytop: vector o escalar con la posición de y arriba.density: número de líneas por pulgada con la cuales se rellenará el rectángulo.angle: ángulo de inclinación de la líneas de relleno.col: color para el fondo del rectángulo.border: color para el borde del rectángulo, un valor posible es'transparent'cuando no se desea borde....: otros parámetros gráficos.
En la Figura 6.2 se muestran 7 rectángulos de ejemplo que fueron obtenidos al variar los parámetros de la función rect, a continuación el código usado para obtener esa figura.
plot(NA, xlim=c(10, 20), ylim=c(10, 30), las=1, xlab='', ylab='')
rect(10, 28, 12, 30)
rect(11, 25, 13, 27, col='red')
rect(12, 22, 14, 24, density=5)
rect(13, 19, 15, 21, density=5, angle=15)
rect(14, 16, 16, 18, col='pink', border='blue')
rect(15, 13, 17, 15, lty='dashed')
rect(16, 10, 18, 12, lwd=3)
text(14, 26, "col='red'")
text(15, 23, "density=5")
text(17, 20, "density=5, angle=15")
text(18.2, 17, "col='pink', border='blue'")
text(18.2, 14, "lty='dashed'")
text(18.8, 11, "lwd=3")
Figure 6.2: Ejemplos de rectángulos.
El código mostrado abajo pertenece a la ayuda de la función rect y el resultado es la Figura 6.3. De esta figura se observa que es posible dibujar varios rectángulos ingresando las coordenadas como vectores.
## set up the plot region:
plot(c(100, 250), c(300, 450), type="n", xlab="", ylab="",
main="2 x 11 rectangles; 'rect(100+i,300+i, 150+i,380+i)'")
i <- 4*(0:10)
## draw rectangles with bottom left (100, 300)+i
## and top right (150, 380)+i
rect(100+i, 300+i, 150+i, 380+i, col=rainbow(11, start=0.7, end=0.1))
rect(240-i, 320+i, 250-i, 410+i, col=heat.colors(11), lwd=i/5)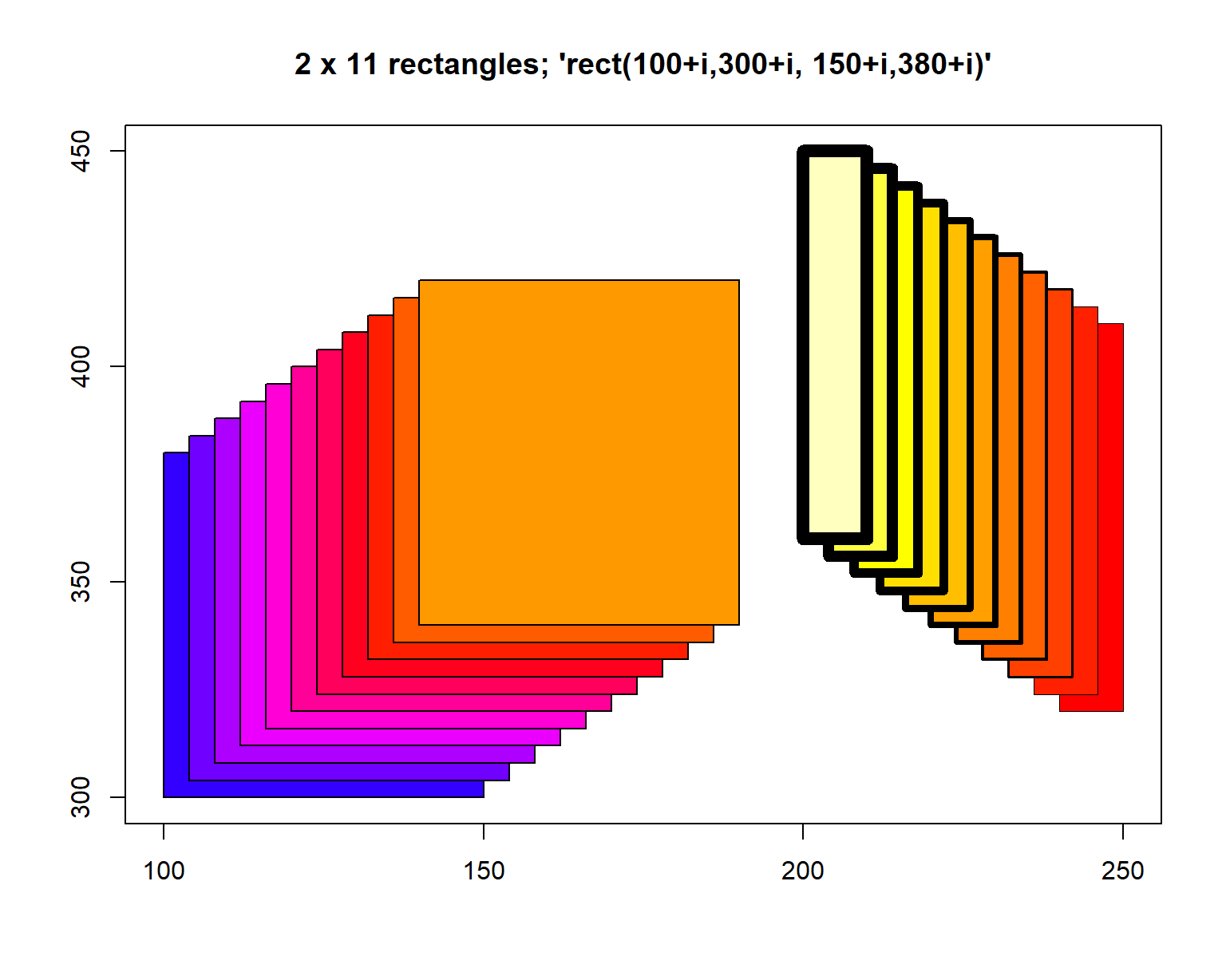
Figure 6.3: Ejemplo de rectángulos obtenidos con rect.
6.3 Función polygon
Esta función es muy útil para dibujar polígonos. La estructura de la función se muestra a continuación.
Los argumentos de la función son:
x, y: vectores con las coordenadas de ubicación de los puntos que forman el polígono.density: número de líneas por pulgada con la cuales se rellenará el polígono.angle: ángulo de inclinación de la líneas de relleno.border: color para el borde del polígono, un valor posible es'transparent'cuando no se desea borde.col: color para el fondo del rectángulo.lty: tipo de línea a usar para el borde....: otros parámetros gráficos.
A continuación se muestra como usar la función polygon para dibujar un triángulo y un cuadrilátero. En la Figura 6.4 se muestran las figuras obtenidas.
plot(0:5, 0:5, type="n", xlab="", ylab="")
abline(v=0:5, h=0:5, col=gray(0.8), lty='dashed')
polygon(x=c(0, 1, 2), y=c(1, 5, 2), # Para el triangulo
col='blue', border='red', lwd=4)
polygon(x=c(3, 5, 5, 2), y=c(5, 4, 1, 1), # Para el cuadrilatero
col='orange', border='darkgreen', lwd=4)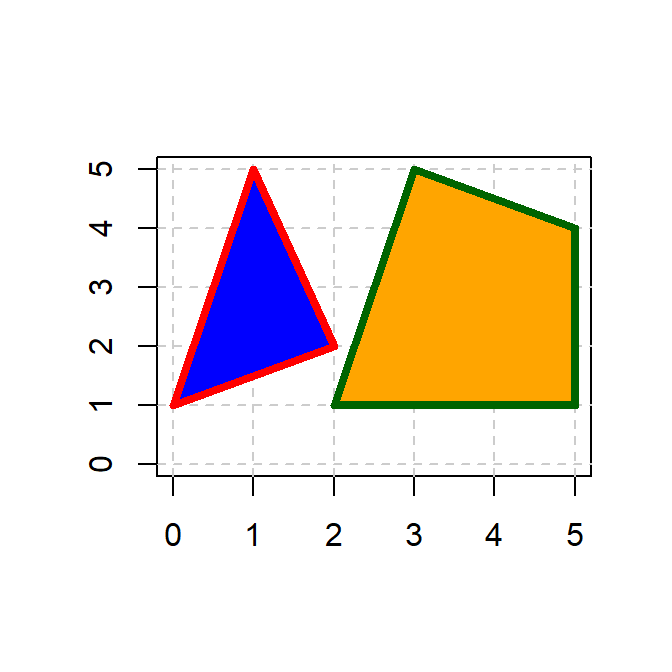
Figure 6.4: Ejemplo de formas obtenidas con polygon.
6.4 Función abline
Esta función es muy útil para dibujar líneas rectas dada la ecuación \(y=a+bx\), donde \(a\) representa el intercepto y \(b\) la pendiente de la recta. La estructura de la función se muestra a continuación.
Los argumentos de la función son:
a, b: son los coeficientes de la ecuación,arepresenta el intercepto ybla pendiente.h: es el valor del eje Y por donde queremos que pase una recta horizontal.v: es el valor del eje X por donde queremos que pase una recta vertical.coef: vector de dos elementos con el intercepto y pendiente.reg: objeto de claselmresultante de haber usado la funciónlm....: otros parámetros gráficos.
A continuación de muestra el código para dibujar la recta \(y=-5+3x\). En la Figura 6.5 se puede ver el resultado.
plot(x=c(-5, 5), y=c(-10, 10), # Para crear el lienzo
xlab="", ylab="", type='n') # donde se ubicará la recta
abline(a=-5, b=3, lwd=3, col='blue')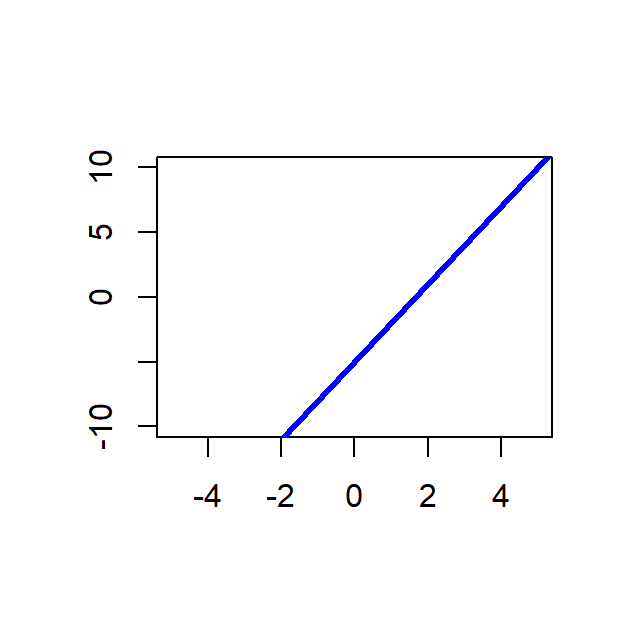
Figure 6.5: Ejemplo de una recta con la función abline.
A continuación de muestra el código para dibujar tres rectas, la de color verde debe ser horizontal y pasar por \(y=5\), la de color rojo debe ser horizontal y pasar por \(y=-3\) y la última debe ser vertical, de color naranja y pasar por \(x=2\). En la Figura 6.6 se puede ver el resultado.
plot(x=c(-5, 5), y=c(-10, 10), # Para crear el lienzo
xlab="", ylab="", type='n') # donde se ubicará la recta
abline(h=c(5, -3), v=2,
col=c('darkgreen', 'red', 'orange'), lwd=5)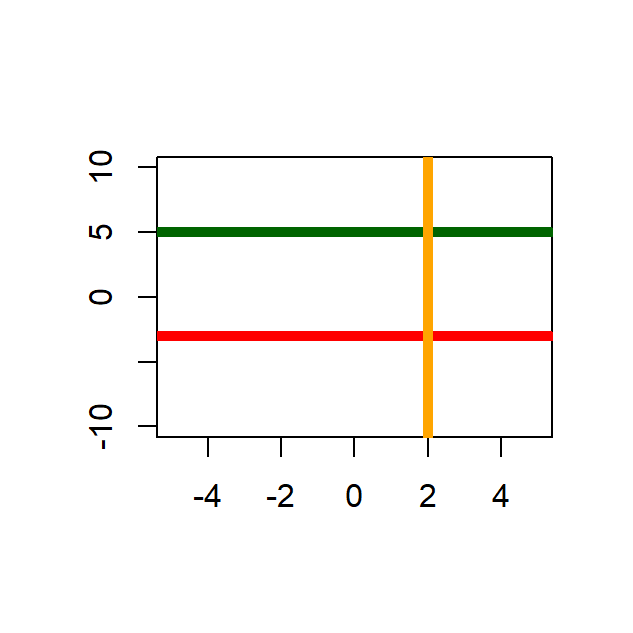
Figure 6.6: Ejemplo de una recta con la función abline.
6.5 Para dibujar un círculo
En la base de R no hay una función específica para crear círculos, sin embargo, es posible usar unas pocas líneas para obtener el círculo con un radio y centro deseado por medio de la función polygon. A continuación se muestra el código para dibujar un círculo de radio 7 unidades con centro en el punto (-2, 1) con fondo azul claro y borde de color azul obscuro. En la Figura 6.7 se muestra el círculo construído.
rad <- 7 # Valor del radio
xcenter <- -2 # Coordenada en x del centro
ycenter <- 1 # Coordenada en y del centro
plot(c(-10, 10), c(-10, 10), type="n", xlab="", ylab="", asp=1)
theta <- seq(0, 2 * pi, length = 200)
polygon(x=rad * cos(theta) + xcenter,
y=rad * sin(theta) + ycenter,
lwd=3, col='steelblue1', border='steelblue4')
grid() # Para incluir una cuadrícula de guía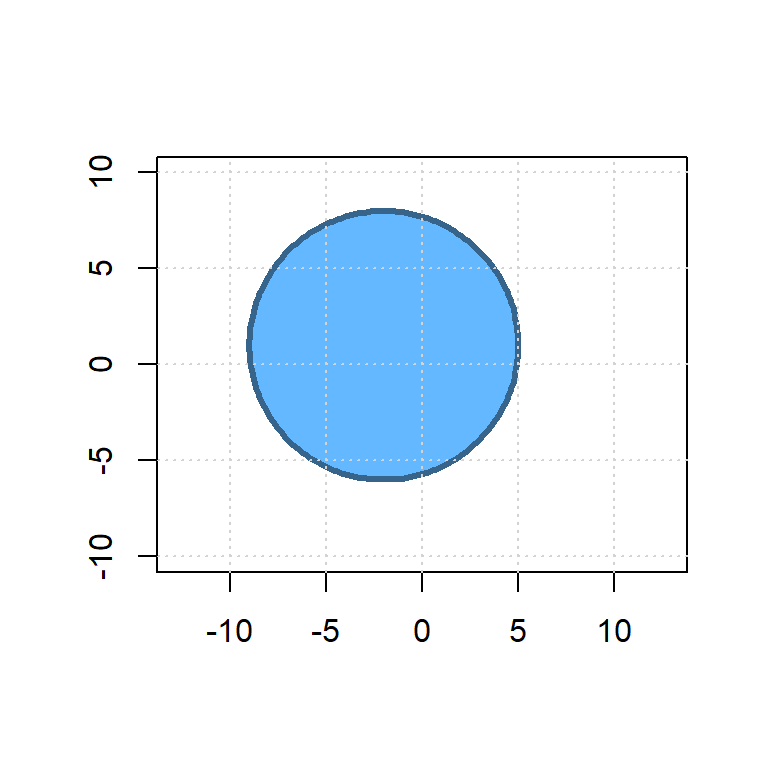
Figure 6.7: Ejemplo de un círculo.
6.6 Función arrows
Esta función es muy útil para incluir flechas en una figura. La estructura de la función se muestra a continuación.
Los argumentos de la función son:
x0, y0: coordenadas de inicio de la flecha.x1, y1: coordenadas de fin de la flecha.length: longitud (en pulgadas) de los bordes de punta de la flecha, el valor por defecto es 0.25.angle: ángulo para la punta de la flecha, a mayor ángulo más abiertas las puntas.code: número entero para indicar el tipo de flecha a dibujar. El valor de 0 para una flecha sin punta (entonces no sería una flecha), el valor de 1 para una flecha apuntando al revés (no es frecuente), el valor de 2 (valor por defecto) para una flecha usual y valor de 3 para colocar puntas a ambos lados de la flecha. El valor por defecto son 30 grados....: otros parámetros gráficos.
En la Figura 6.8 se muestran los cuatro tipos de flechas que se obtienen al variar el parámetro code de la función arrows. Note que la flecha de la derecha fue construída subiendo, pero como code=1 ella quedó bajando.
plot(NA, xlab='X', ylab='Y', # Para crear un gráfico vacío
xlim=c(0, 6), ylim=c(0, 5))
arrows(x0=2, y0=1, x1=4, y1=1, code=0)
arrows(x0=5, y0=1, x1=5, y1=4, code=1)
arrows(x0=2, y0=4, x1=4, y1=4, code=2)
arrows(x0=1, y0=1, x1=1, y1=4, code=3)
text(3, 0.8, 'code=0')
text(5.4, 2.5, 'code=1')
text(3, 4.2, 'code=2')
text(0.6, 2.5, 'code=3')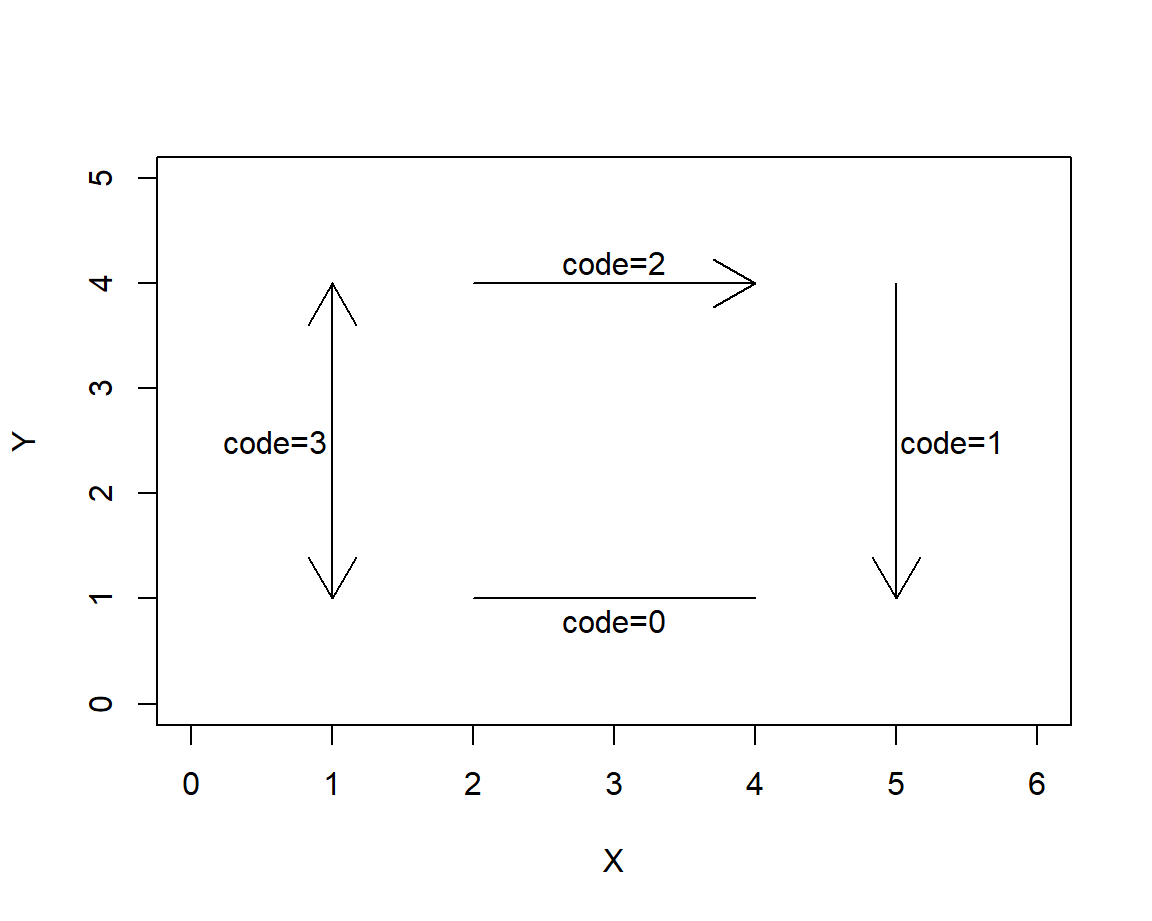
Figure 6.8: Ejemplos de flechas variando el parámetro code.
En la Figura 6.9 se muestran 4 flechas para varios valores del parámetro angle, de la figura se observa que entre mayor el ángulo, la punta de la fecha es más achatada.
plot(NA, xlab='X', ylab='Y', # Para crear un gráfico vacío
xlim=c(0, 6), ylim=c(0, 5))
arrows(x0=1, y0=4, x1=4, y1=4)
arrows(x0=1, y0=3, x1=4, y1=3, angle=45)
arrows(x0=1, y0=2, x1=4, y1=2, angle=60)
arrows(x0=1, y0=1, x1=4, y1=1, angle=90)
text(4.5, 3, 'angle=45')
text(4.5, 2, 'angle=60')
text(4.5, 1, 'angle=90')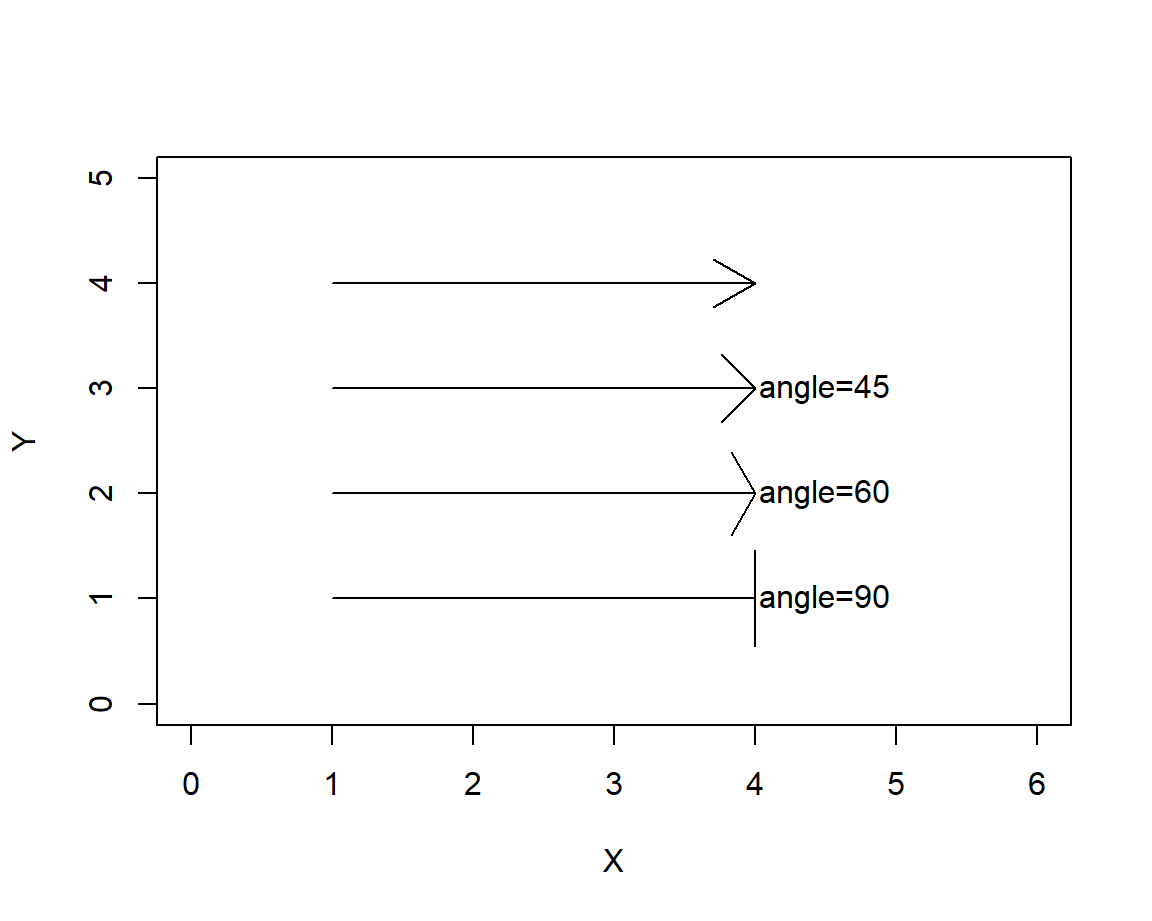
Figure 6.9: Ejemplos de flechas variando el parámetro angle.
6.7 Función grid
La función grid es muy útil para construir rejillas sobre un gráfico, estas rejillas se pueden usar como referencia para facilitar la interpretación o como guía para ubicar elementos en un dibujo.
La estructura de la función se muestra a continuación.
Los argumentos de la función son:
nx, ny: número de celdas a dibujar tanto en el eje horizontal y vertical.col: color de la rejilla.lty: tipo de línea a usar.lwd: grosor de la rejilla.
A continuación se muestran dos ejemplos de como usar grid. En el primer ejemplo se dibuja un gráfico vacío y se le agrega la rejila estándar que se puede obtener con grid() sin definir ningún parámetro. En el segundo ejemplo se tiene una rejilla que divide en 4 partes el eje horizontal (nx=3), en 4 partes el eje vertical (ny=4), de color rosado, grosor 2 y con guiones largos. Abajo el código utilizado y en la Figura 6.10 se observan los resultados.
par(mfrow=c(1, 2), mar=c(2, 2, 0, 0), cex=0.5)
plot(c(-10, 10), c(-10, 10), type="n", xlab="", ylab="")
grid()
plot(c(-10, 10), c(-10, 10), type="n", xlab="", ylab="")
grid(nx=3, ny=4, col="pink", lwd=2, lty="longdash")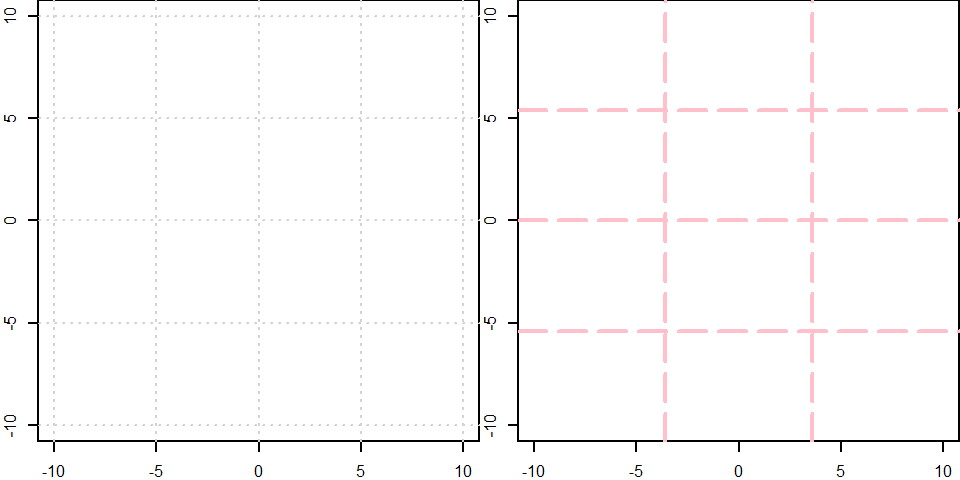
Figure 6.10: Ejemplos de rejillas con grid.
6.8 Función points
Esta función es útil para agregar puntos a una figura ya creada. La estructura de la función es la siguiente.
Los argumentos de la función son:
x, y: vectores con las coordenadas de ubicación de los puntos.pch: valor o vector numérico con el tipo de punto a usar, por defectopch=1.col: vector con los colores para cada punto.cex: número para modificar el tamaño de los puntos, por defecto escex=1y al aumentar su valor aumenta el tamaño de los puntos.
Los diferentes tipos de puntos que se pueden obtener al variar el parámetro pch se muestran en la Figura 6.11.

Figure 6.11: Ejemplos de los tipos de puntos obtenidos al variar pch.
Es posible usar otros símbolos personalizados en el parámetro pch, a continuación se muestra el código para incluir 5 puntos usando los símbolos @, ., $, % y w. En la Figura 6.12 se observan los 5 puntos con los símbolos usados. Observe que cuando se usó pch='.' aparece un pequeño punto, casi imperceptible, esta opción es muy usada cuando se tiene muchos puntos que se traslapan entre si.
par(mar=c(2, 2, 0, 0))
plot(c(0.5, 5.5), c(0.5, 5.5), xlab="", ylab="", type='n')
points(x=1:5, y=1:5,
pch=c('@', '.', '$', '%', 'w'),
col=1:5)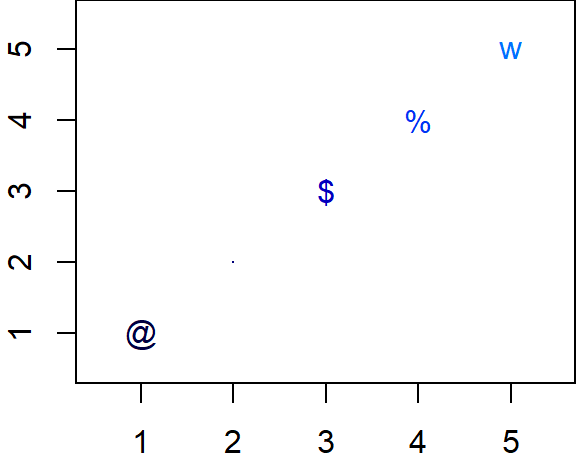
Figure 6.12: Ejemplos de símbolos personalizados con pch.
6.9 Función curve
Esta función sirve para dibujar una curva en un intervalo dado. La estructura de la función es la siguiente.
Los argumentos de la función son:
expr: nombre de la función que se desea evaluar.from, to: valores mínimo y máximo donde se va a evaluar la función.n: número de puntos en los cuales se va a evaluar la función, su valor por defecto es 101.add: valor lógico para indicar que se desea agregar la curva a un gráfico ya existente.type: tipo de representación para la función, se disponen de 9 opciones que se pueden consultar en descripción detypepara la funciónploten la sección @ref(par_type).xlim: intervalo para construir la ventana gráfica, no confundir confromyto.
Ejemplo
Dibujar las funciones \(f_1\), \(f_2\) y \(f_3\) usando la función curve, las ecuaciones para las funciones son:
\[\begin{align} f_1(x) &= x^2-10 \\ f_2(x) &= \begin{cases} x^2-10, & \mbox{si } x < 1 \\ 5 x, & \mbox{si } x \geq 1 \end{cases} \\ f_3(x) &=15-4x \end{align}\]
Dibujar \(f_1\) en el intervalo [-2, 7], \(f_2\) en el intervalo [-2, 4] y \(f_3\) en el intervalo [-5, 0].
El código necesario para definir las dos funciones se muestra a continuación. Para dibujar \(f_2\) y \(f_3\) se usó add=TRUE con el objetivo de que quedaran en la misma ventana gráfica de \(f_1\). Note que se usó xlim=c(-5, 10) para indicar que se deseaba una ventana gráfica en ese intervalo para el eje horizontal. En la Figura 6.13 se muestra el dibujo de las tres funciones.
f1 <- function(x) x^2 - 10
f2 <- function(x) ifelse(x < 1, -x^2, 5*x)
f3 <- function(x) 15 - 4 * x
curve(expr=f1, from=-2, to=7, type="l",
col="blue", lwd=4, ylab='f(x)', xlim=c(-5, 10))
curve(expr=f2, from=-2, to=4, type="p",
col="green4", add=TRUE)
curve(expr=f3, from=-5, to=0, type="b",
col='red', add=TRUE, n=5)
text(x=7, y=9, "f1(x) usando type='l'", col="blue")
text(x=-2, y=4, "f2(x) usando type='p'", col="green4")
text(x=-1, y=30, "f3(x) usando type='b' y n=5", col="red")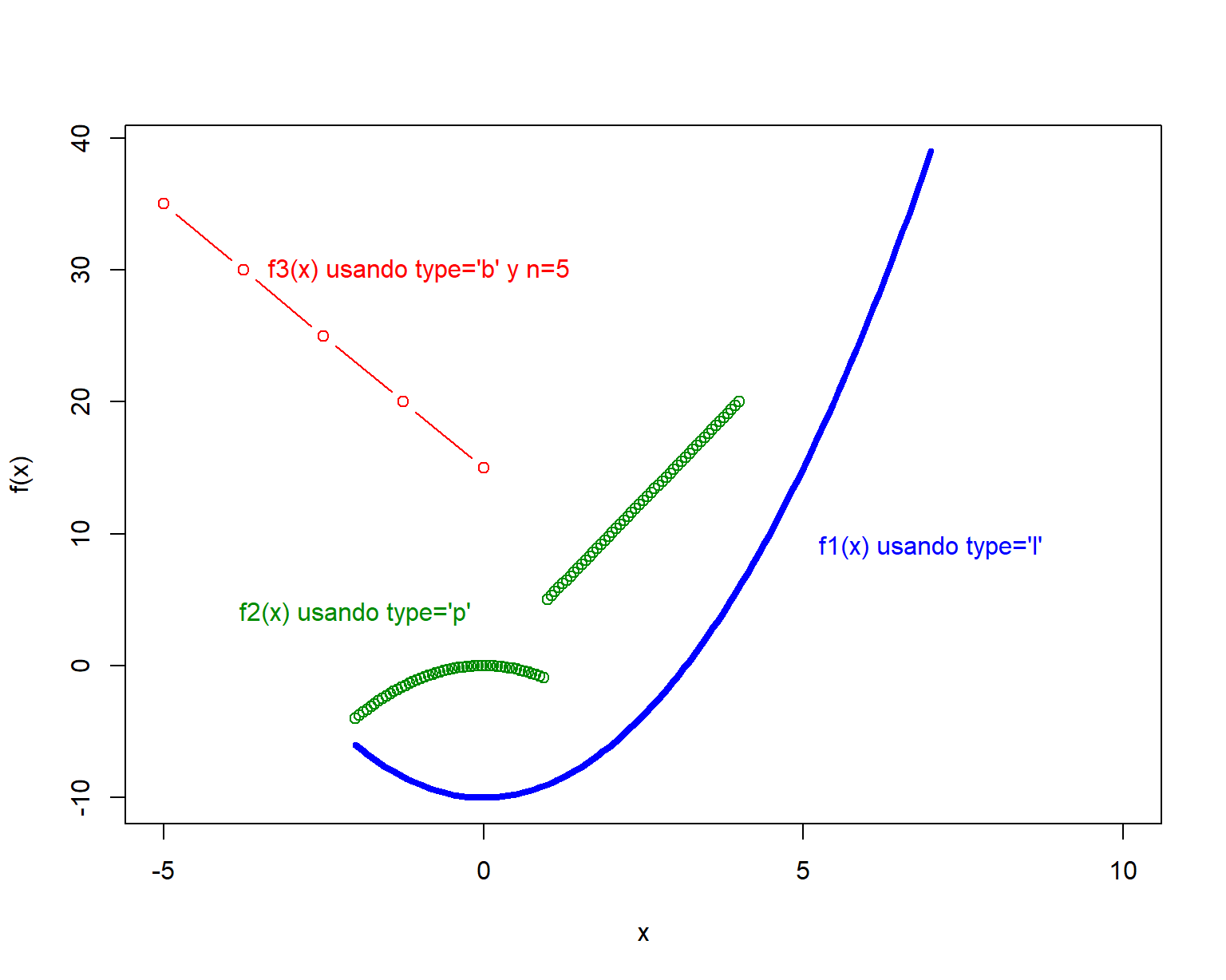
Figure 6.13: Dibujo de varias funciones en una misma ventana.
Ejemplo
Dibujar la figura de la relación entre las variables \(x\) y \(y\) dada por la siguiente expresión paramétrica:
\[\begin{align} x &= 16 \cos^3(t) \\ y &= 13 \cos(t)-5 \cos(2t)-2 \cos(3t)- \cos(4t) \end{align}\]
El código para realizar la Figura 6.14 fue tomado de Stackoverflow y se muestra a continuación.
dat <- data.frame(t=seq(0, 2*pi, by=0.1))
xhrt <- function(t) 16*sin(t)^3
yhrt <- function(t) 13*cos(t)-5*cos(2*t)-2*cos(3*t)-cos(4*t)
dat$y <- yhrt(dat$t)
dat$x <- xhrt(dat$t)
with(dat, plot(x,y, type="l", lwd=10))
with(dat, polygon(x, y, col="hotpink"))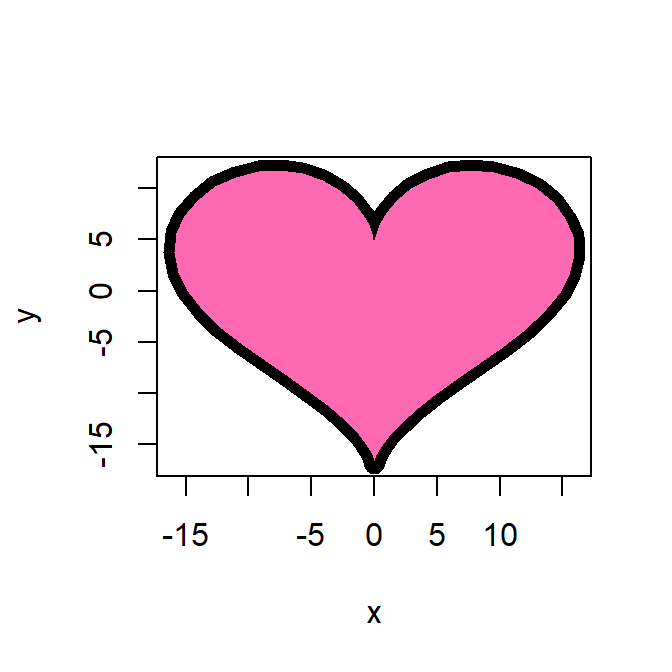
Figure 6.14: Dibujo de un cardiode.
EJERCICIOS
Crear un gráfico vacío de manera que el eje horizontal tome valores desde 0 a 30 y el eje vertical valores de 0 a 20, usar los pasos de la sección 7.1 para construir el gráfico solicitado.
Para el gráfico vacío creado en el paso anterior, agregar una rejilla o cuadrícula que pase por los valores enteros, use los pasos de la sección 7.6 para incluir la rejilla en los valores solicitados. El gráfico resultante de los ejercicios 1 y 2 debe ser similar al presentando en la Figura 6.15.
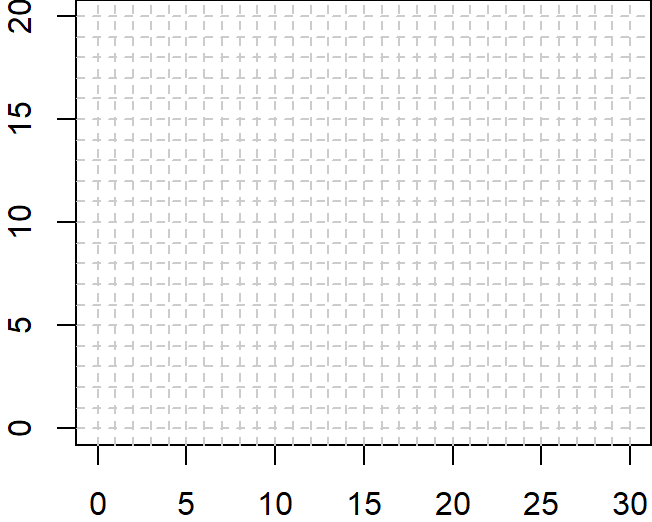
Figure 6.15: Plantilla para el dibujo.
- Incluir en el gráfico vacío y con rejillas anterior el dibujo mostrado en la Figura 6.16. Use las funciones vistas en este capítulo para replicar el dibujo del paisaje e incluya colores para mejorar la apariencia del paisaje.
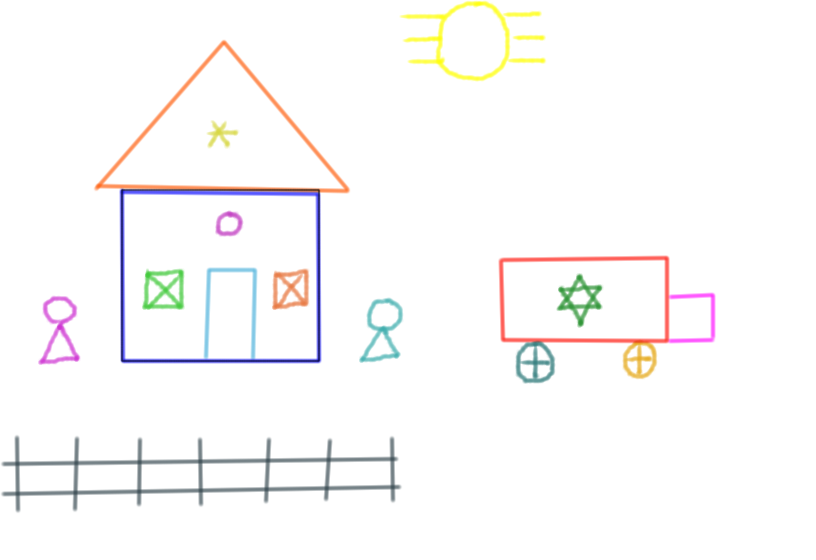
Figure 6.16: Paisaje a dibujar.
Dibujar las siguientes dos líneas en un mismo gráfico, la primera de color azul y la segunda de color verde. \[\begin{align*} 2x - 5y &= 8 \\ 3x + 9y &= -12 \end{align*}\]
Dibujar la siguiente figura dada en forma parametrica. \[\begin{align*} x &= \cos(t) \\ y &= \sin(t) \end{align*}\]