This function can be used to test \(H_0: \mu = \mu_0\) versus \(H_1: \mu\) not = \(\mu_0\) under \(\Sigma\) known or unkwon.
one_mean_vector_test(mu0, xbar, n, S = NULL, Sigma = NULL)Arguments
Value
A list with class "htest" containing the following components:
- statistic
the value of the statistic.
- parameter
the degrees of freedom for the test.
- p.value
the p-value for the test.
- estimate
the estimated covariance matrix S.
- alternative
a character string describing the alternative hypothesis.
- method
a character string indicating what type of test was performed.
Details
The user must provide only one matrix, S to perform the T2 test or \(\Sigma\) to perform the X2 test. When \(\Sigma\) is unkwon, T2 is perform and two values are provided in the print output, the T2 and F value.
See also
one_covar_matrix_test for test \(\Sigma\) in a \(Np(\mu, \Sigma)\).
Examples
# Example 5.2.2 from Rencher & Christensen (2012) page 127
# Test H0: mu = (70, 170) versus H1: mu != (70, 170)
# with known Sigma
Sigma <- matrix(c(20, 100, 100, 1000), ncol=2, nrow=2)
res1 <- one_mean_vector_test(mu0=c(70, 170), xbar=c(71.45, 164.7),
n=20, Sigma=Sigma)
res1
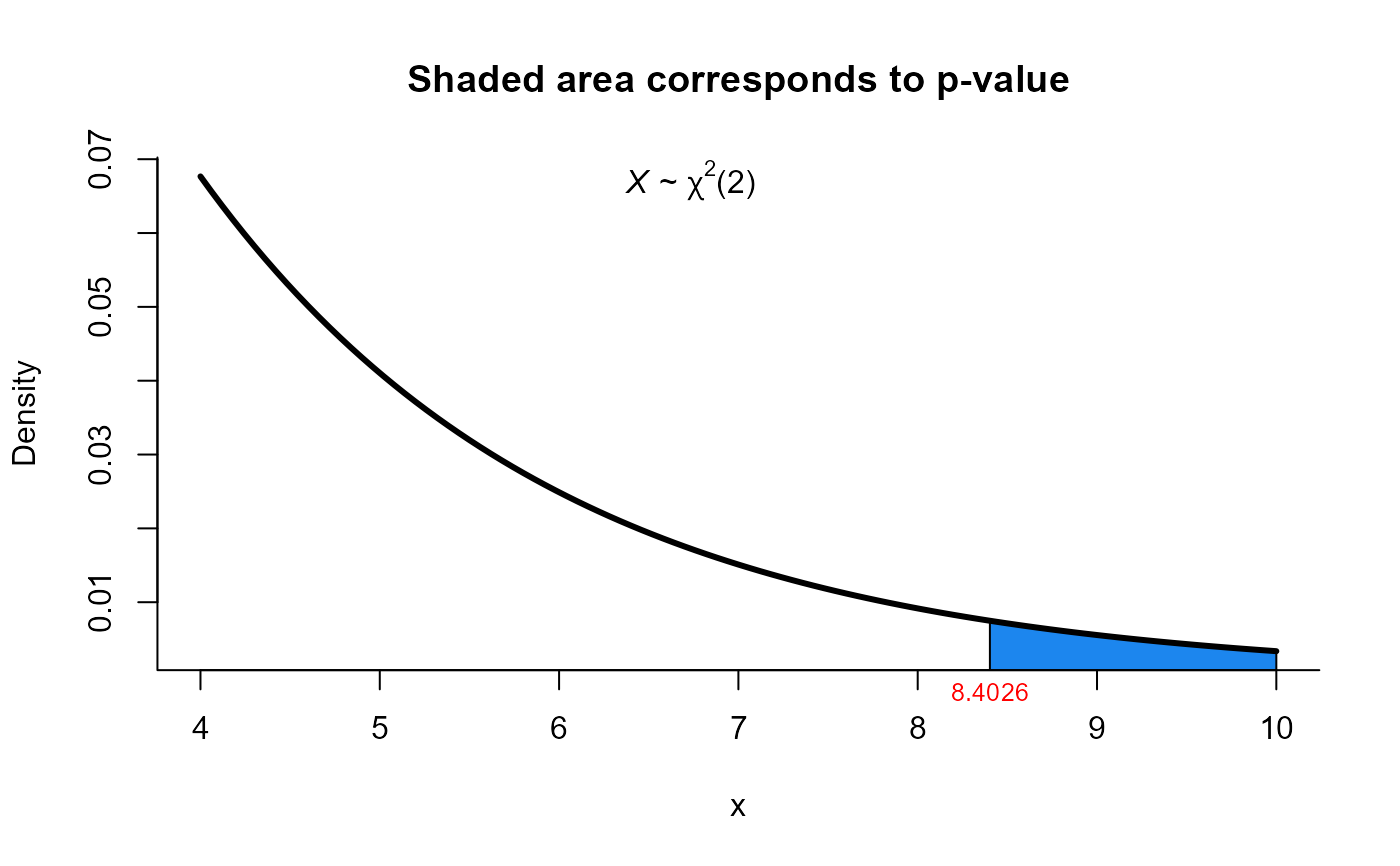
#>
#> X2 test for mean vector
#>
#> data: this test uses summarized data
#> X2 = 8.4026, df = 2, p-value = 0.01498
#> alternative hypothesis: true mean vector is not equal to (70, 170)
#>
#> sample estimates:
#> xbar_1 xbar_2
#> 71.45 164.70
#>
plot(res1, from=4, to=10, shade.col='dodgerblue2')
 # Repeating the last example with raw data
x1 <- c(69, 74, 68, 70, 72, 67, 66, 70, 76, 68,
72, 79, 74, 67, 66, 71, 74, 75, 75, 76)
x2 <- c(153, 175, 155, 135, 172, 150, 115, 137, 200, 130,
140, 265, 185, 112, 140, 150, 165, 185, 210, 220)
dt <- data.frame(x1, x2)
mu0 <- c(70, 170)
Sigma <- matrix(c(20, 100, 100, 1000), ncol=2, nrow=2)
res2 <- one_mean_vector_test(mu0=mu0, xbar=colMeans(dt),
n=nrow(dt), Sigma=Sigma)
res2
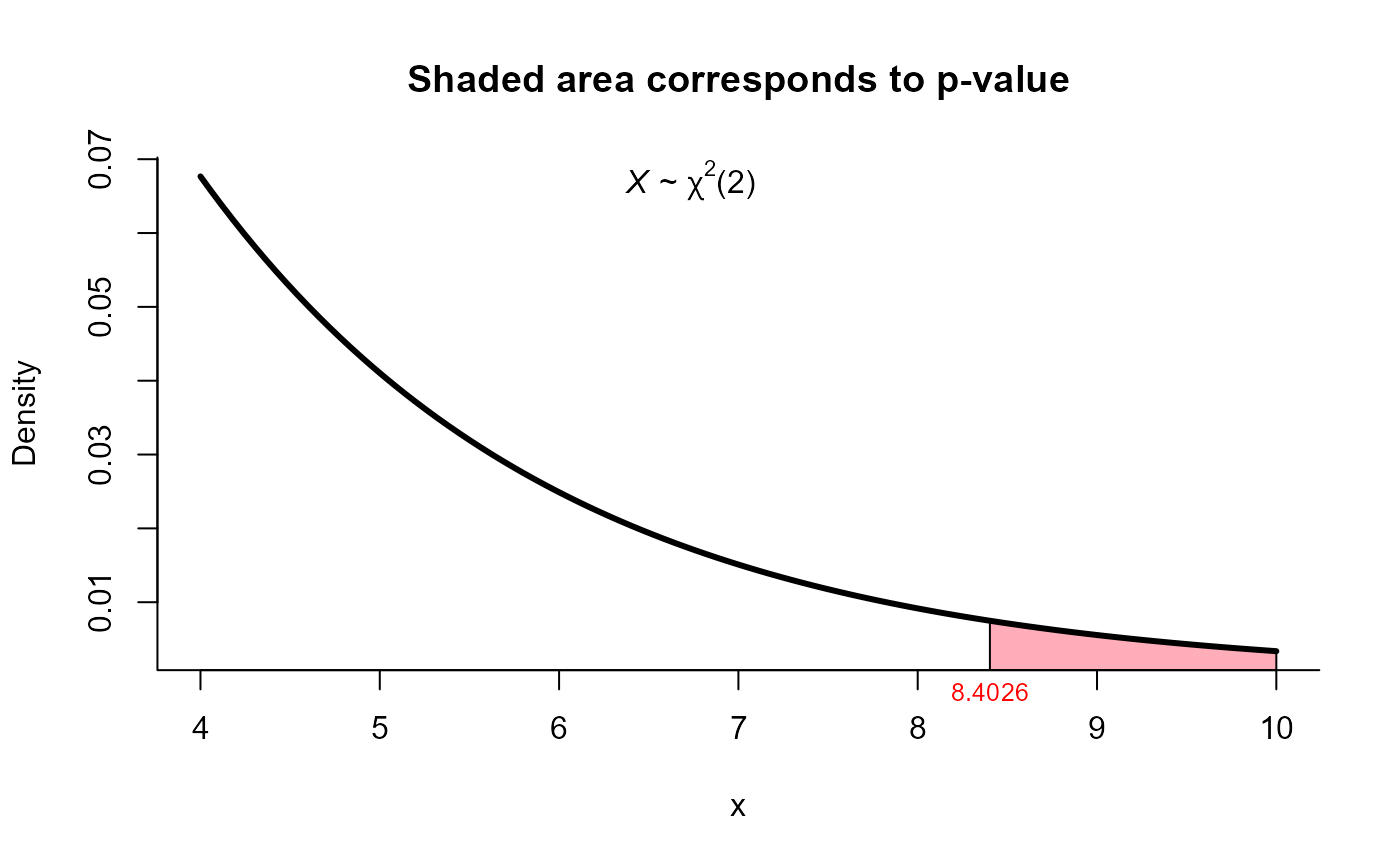
#>
#> X2 test for mean vector
#>
#> data: this test uses summarized data
#> X2 = 8.4026, df = 2, p-value = 0.01498
#> alternative hypothesis: true mean vector is not equal to (70, 170)
#>
#> sample estimates:
#> xbar_1 xbar_2
#> 71.45 164.70
#>
plot(res2, from=4, to=10, shade.col='lightpink1')
# Repeating the last example with raw data
x1 <- c(69, 74, 68, 70, 72, 67, 66, 70, 76, 68,
72, 79, 74, 67, 66, 71, 74, 75, 75, 76)
x2 <- c(153, 175, 155, 135, 172, 150, 115, 137, 200, 130,
140, 265, 185, 112, 140, 150, 165, 185, 210, 220)
dt <- data.frame(x1, x2)
mu0 <- c(70, 170)
Sigma <- matrix(c(20, 100, 100, 1000), ncol=2, nrow=2)
res2 <- one_mean_vector_test(mu0=mu0, xbar=colMeans(dt),
n=nrow(dt), Sigma=Sigma)
res2
#>
#> X2 test for mean vector
#>
#> data: this test uses summarized data
#> X2 = 8.4026, df = 2, p-value = 0.01498
#> alternative hypothesis: true mean vector is not equal to (70, 170)
#>
#> sample estimates:
#> xbar_1 xbar_2
#> 71.45 164.70
#>
plot(res2, from=4, to=10, shade.col='lightpink1')
 # Example 5.2 from Johnson and Wichern (2012) page 214
# Test H0: mu = (4, 50, 10) versus H1: mu != (4, 50, 10)
# with unknown Sigma
S <- matrix(c(2.879, 10.010, -1.810,
10.010, 199.788, -5.640,
-1.810, -5.640, 3.628), ncol=3, nrow=3)
res3 <- one_mean_vector_test(mu0=c(4, 50, 10),
xbar=c(4.640, 45.400, 9.965),
n=20, S=S)
res3
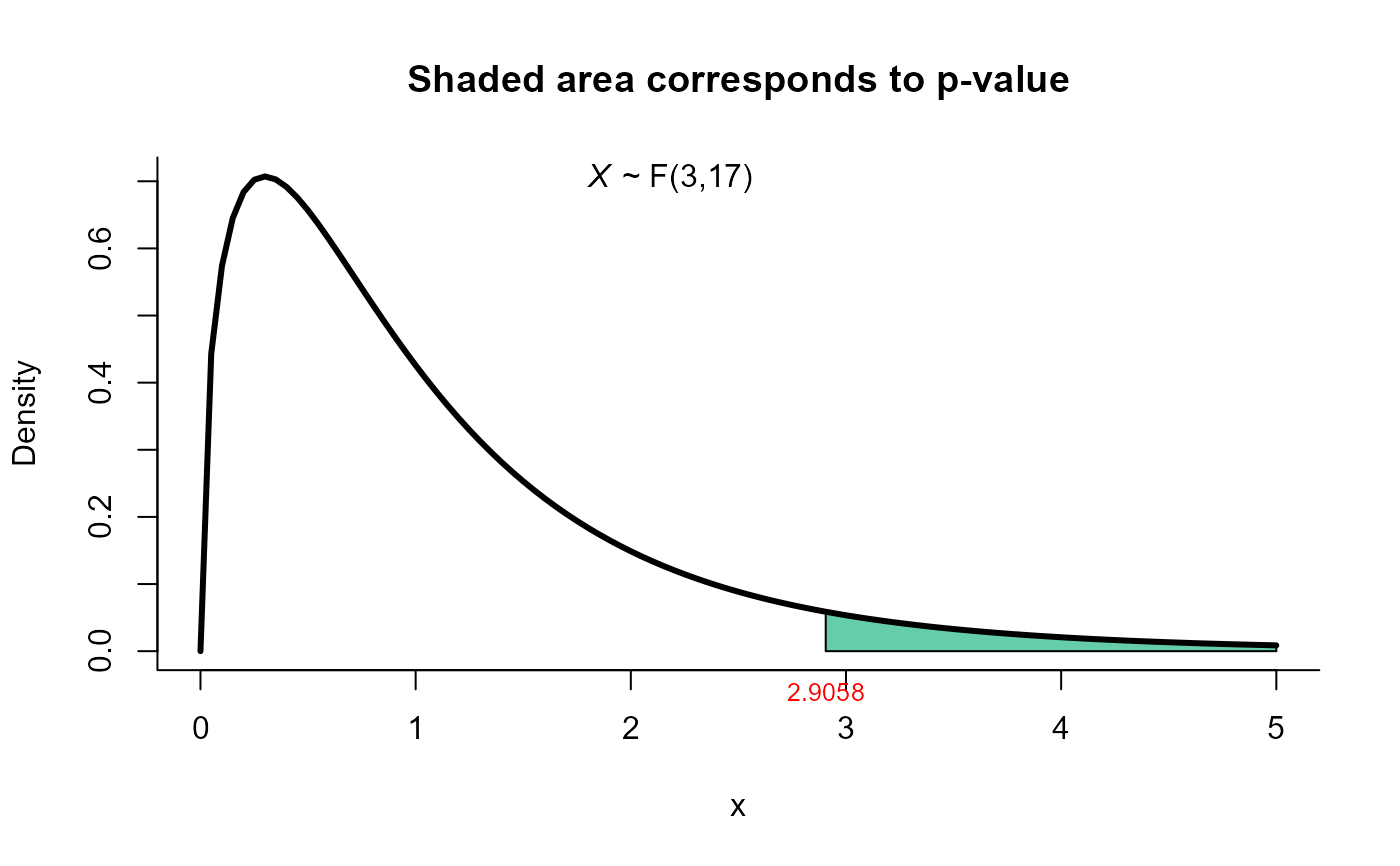
#>
#> T2 test for mean vector
#>
#> data: this test uses summarized data
#> T2 = 9.7430, F = 2.9058, df1 = 3, df2 = 17, p-value = 0.06485
#> alternative hypothesis: true mean vector is not equal to (4, 50, 10)
#>
#> sample estimates:
#> xbar_1 xbar_2 xbar_3
#> 4.640 45.400 9.965
#>
plot(res3, from=0, to=5, shade.col='aquamarine3')
# Example 5.2 from Johnson and Wichern (2012) page 214
# Test H0: mu = (4, 50, 10) versus H1: mu != (4, 50, 10)
# with unknown Sigma
S <- matrix(c(2.879, 10.010, -1.810,
10.010, 199.788, -5.640,
-1.810, -5.640, 3.628), ncol=3, nrow=3)
res3 <- one_mean_vector_test(mu0=c(4, 50, 10),
xbar=c(4.640, 45.400, 9.965),
n=20, S=S)
res3
#>
#> T2 test for mean vector
#>
#> data: this test uses summarized data
#> T2 = 9.7430, F = 2.9058, df1 = 3, df2 = 17, p-value = 0.06485
#> alternative hypothesis: true mean vector is not equal to (4, 50, 10)
#>
#> sample estimates:
#> xbar_1 xbar_2 xbar_3
#> 4.640 45.400 9.965
#>
plot(res3, from=0, to=5, shade.col='aquamarine3')
 if (FALSE) { # \dontrun{
library(rrcov)
data(delivery)
delivery.x <- delivery[, 1:2]
# Using T2.test from rrcov package
T2.test(delivery.x)
one_mean_vector_test(mu0=c(0, 0), xbar=colMeans(delivery.x),
n=25, S=var(delivery.x))
} # }
if (FALSE) { # \dontrun{
library(rrcov)
data(delivery)
delivery.x <- delivery[, 1:2]
# Using T2.test from rrcov package
T2.test(delivery.x)
one_mean_vector_test(mu0=c(0, 0), xbar=colMeans(delivery.x),
n=25, S=var(delivery.x))
} # }